基于驻留时间比的近地空间碎片环境建模

申敬松

(北京航空航天大学 宇航学院，北京100191)

刘 也* 胡松杰

(北京航天飞行控制中心 航天飞行动力学技术重点实验室，北京100094)

韩 潮

(北京航空航天大学 宇航学院，北京100191)

人类开发太空的脚步给空间带来了大量的碎片累积，这些碎片主要分布在近地轨道和同步轨道，具有高速运动和分布随机化的特征，给在轨正常运行的航天器，特别是长期运行的载人航天器带来了极大的安全隐患［1-2］.因此，对于需长期运行于低地轨道的载人航天器来说，为评估碎片碰撞带来的安全风险并采取有效的预防措施，需要有效描述碎片分布和演化规律的环境建模技术的支持［2-3］.

空间碎片环境建模的方法主要是利用已有观测数据，综合考虑航天器区域分布和碎片的尺寸、速度、碰撞角和来源等因素，并在一定简化假设下，借助数据拟合和概率统计等建立的［4］.已公开提供的模型按计算方式可以分为演化模式和工程模式，前者立足于采用分析手段刻画空间碎片分布的演化规律，但其建模精度依赖于碎片分布影响因素的有效认识，这在目前理论知识下还是很难实现的.工程模式则依据碎片测量数据建模，可以给出比较准确的碎片分布和碰撞风险情况，适合分析空间环境的综合影响，已广泛服务于航天器设计、操控和为碎片观测计划制定等工程任务［1，3］，如美国国家宇航局(NASA)、欧洲空间局(ESA)、俄罗斯国家宇航局(RASA)的ORDEM，MASTER和SDPA等系列模型［5-6］.其中 NASA的 ORDEM 模型已更新到ORDEM2010，并在官方网站公开提供了ORDEM2000的免费版本［7-8］.

国内方面，一些单位也开展了空间碎片工程模式的分析和建模工作［3-5，9-10］，但由于可用数据限制和研究起步较晚的缘故，许多科学研究和工程实践还依赖于国外公开的环境模型.为此，本文针对低轨载人航天器长期在轨运行需求，试图通过碎片轨道测量数据统计分析，建立一种实用性较强的低轨空间碎片环境建模方法，并通过建模实例进行碎片时空分布规律的分析，以期为航天器碰撞风险评估与防护设计等工作提供借鉴.

1 碎片环境建模流程

1.1 碎片初选

碎片环境模型是描述近地轨道空间碎片三维分布特性的，且需要考虑其随时间的变化情况.为便于统计分析，需要进行时空的离散化，并进行区域内碎片(也包含正常飞行目标)的遴选.

碎片的数量和分布是受航天发射、在轨解体与碰撞、大气阻力和人为缓解(如回收)等因素综合影响的，其中航天发射和大气阻力等都是随季节变化的，因此，鉴于统计时间与模型粒度和准确性的关系，这里以季度为基本时间单元统计碎片分布状况.

空间的划分相对简单，对于近地空间可以按照距地面高度h、纬度φ和经度λ做出三维的网格划分.为了处理球壳两极附近的网格，引入最大纬度φ0，将每个高度层内大于φ0的网格合并为同一网格.网格划分要兼顾计算量、存储量和精度等要素，也可以引入相邻高度层的网格比例，以调节不同高度层网格的大小.

碎片初选是为了剔除明显不会飞入所考察空域的碎片.对于高度区域［hmin，hmax］，当碎片轨道近地点高度大于hmax或远地点高度小于hmin，碎片才可能进入该高度层.例如TLE(Two Line Elements)编目数据可提供目标的偏心率e和角速度n，记地球物理常数 μ，平均半径r0，则可得穿越［hmin，hmax］的碎片需满足的角速度取值范围［nmin，nmax］:

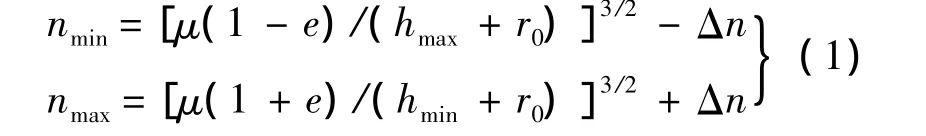
其中Δn是为了补偿球形地球和瞬时圆轨道假设的误差，保证初选碎片不出现漏警.

1.2 建模流程

在模型覆盖时空多维离散化的基础上，利用经过初选的编目碎片数据，设计了如图1所示的建模流程.基本过程分为3个步骤:

1)根据数据更新频率和精度进行轨道预报，并计算与该段轨道交会的网格及交会起止时间;

2)在基本时间单元内(季度)，统计碎片在各网格内的驻留(飞行)时间和通量，获得工程模式所需的基础数据源;

3)根据应用需求，内嵌一系列数据插值和时间序列分析等方法，输出应用模型所需的结果.

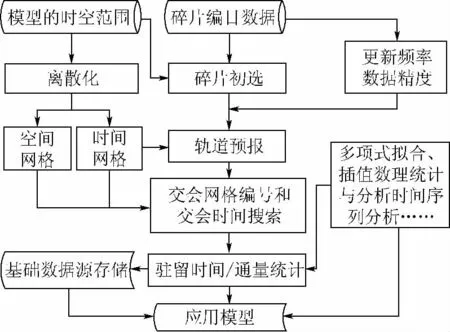
图1 空间碎片环境建模流程Fig.1 Modeling diagram for space debris environment

2 碎片环境建模方法

2.1 碎片分布

下面采用搜索方式，依次在高度维、纬度维和经度维寻找与碎片交会的网格及起止时刻.

对碎片j第s段预报轨道，根据轨道时空连续性特点，可将其划分为若干拟合区间［ti，s，ti+1，s］.对第 i 个 区 间 的 高 度 数 据，记 ai，sh3+bi，sh2+ci，sh+di，s=0 为其三次多项式拟合结果.为便于时间统计，需要将拟合区间划分为几个单调区间.导数方程求根得极值时刻ti1，s=［-2b+(4b2-12ac)1/2］/6a 与 ti2，s=［-2b-(4b2-12ac)1/2］/6a.进而可分为如下4种情况:

1)ti1，s与 ti2，s均在区间内，此时轨道按高度可划分 单 调 区 间 ［ti，s，ti1，s］，［ti1，s，ti2，s］与 ［ti2，s，ti+1，s］;

2)ti1，s不在区间内，此时轨道按高度可划分单调区间［ti，s，ti2，s］与［ti2，s，ti+1，s］;

3)ti2，s不在区间内，此时轨道按高度可划分单调区间［ti，s，ti1，s］与［ti1，s，ti+1，s］;

4)ti1，s与 ti2，s均不在区间内，此时轨道按高度为一个单调区间［ti，j，ti+1，j］.

对每个单调区间［tb，te］对应的［hb，he］，根据设定的高度划分Δh来搜索与其交会的高度层.若高度层［hm，hm+Δh］⊂［hb，he］，则根据三次方程求根公式［11］和根的范围可计算交会时间［th，m，th，m+1］.同样的，对［th，m，th，m+1］内的纬度数据采用类似的拟合、划分单调区间和求根步骤，可获得碎片交会的纬度维编号 n及起止时间［tφ，n，tφ，n+1］.进一步，同样可计算［tφ，n，tφ，n+1］内碎片交会的经度维编号 k 及起止时间［tλ，k，tλ，k+1］.

综上，就搜索到了与碎片交会的网格在高度、纬度与经度编号(m，n，k)，可计算驻留时间为

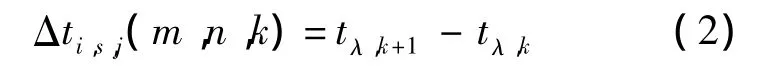
记该时间单元(季度)总时间T，对s，j和i求和，可得碎片驻留时间比:

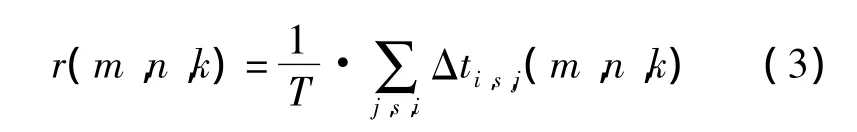
航天器在空域中的碰撞风险分析常用到碎片通量的概念，它可以定义为该处碎片数量密度与速度的乘积［5］.通量方向由航天器和碎片相对速度方向决定，通常惯性空间一点的通量分为单方向通量和各方向全通量.当不考虑特定航天器时，可以采用全通量方式(即各方向通量之和)刻画碎片特征，此时若假设每个网格内碎片速度是常值，记网格体积为V(m，n，k)，则可计算碎片的全通量:

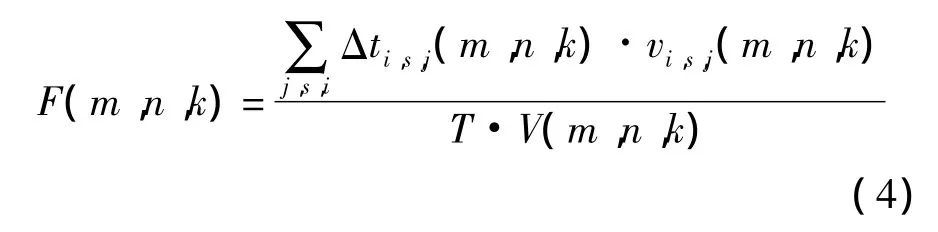
式(4)若不考虑网格体积，则为网格内的碎片通量.当分析具体航天器的轨道时，在精度要求不高的情况下，在近地轨道区域可以认为单个位置的空间碎片通量全部集中在该位置的当地水平面内，如 ORDEM2000 工程模式［3］.

2.2 模型数据

模型的基础数据源就是统计的碎片驻留时间和通量，可以将每个时间单元的统计结果存储为一个基本文件.为了节省存储空间，文件内除包含必要的时空网格参数，只需按顺序存储量化后的各网格的驻留时间比和碎片通量.顺序存储的数据也便于开发辅助工具进行可视化等处理.

进一步，为适应精简模型的应用需求，在参数合理设定的基础上，对碎片驻留时间比和通量进行分段的三维多项式拟合，并仅存储多项式系数.这样就大大减少了模型的存储量和预处理时间，而应用时可利用这些参数快速恢复驻留时间比与通量等数据，或直接进行其他参数的计算.

2.3 模型分析

驻留时间比 r(m，n，k)刻画了网格(m，n，k)出现碎片的概率，记网格体积为V(m，n，k)，可得空间密度:

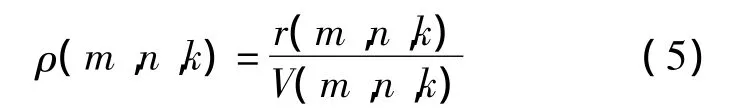
多数的空间碎片处于无主动机动状态，长期的轨道进动会使碎片在经度上趋于均匀分布.此外，航天发射场的纬度分布导致了碎片轨道倾角的分布具有峰值特性，这会表现在碎片空域的纬度分布上［12］，故对于刻画长期演化规律，可计算高度-纬度带内的平均空间密度:

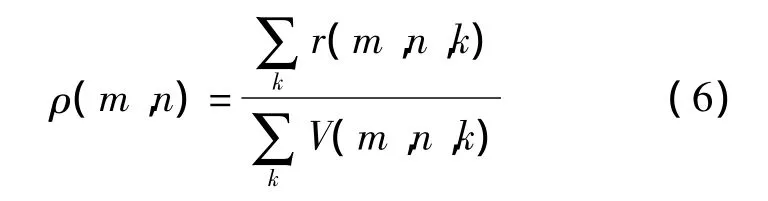
低轨载人航天器通常飞行在高度相对固定的近圆轨道，空间碎片环境分析时也通常给出各个高度层内的碎片分布，如ORDEM模型［7-8］.记高度层［hb，he］的体积为 V(b，e)，可以统计该高度层内的平均空间密度:类似地，为航天器长期运行的碰撞风险综合评估提供参考，可以统计各个层次的碎片平均速度和通量等.特别地，给定航天器轨道oL和周期TL(L代表近地轨道卫星)，航天器轨道周期内的平均碎片通量计算如下:

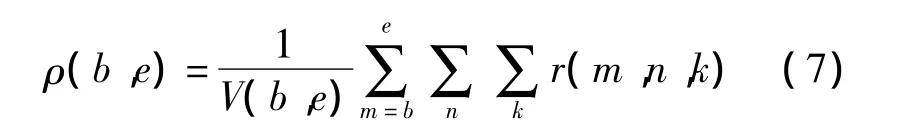
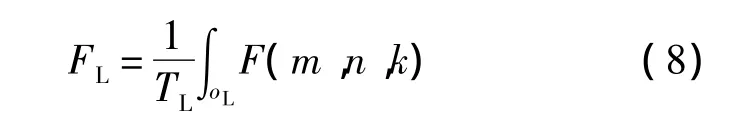
根据所存储的分季度网格数据，在空间上采用三次多项式插值，可以给出该季度模型覆盖空域内任意空间位置的碎片驻留时间，也就可以给出任意位置的碎片密度、平均速度和通量等.这与ORDEM模型的地基观测视角［7］类似，只是时空划分更加细致，但由于数据源限制，未给出分布与碎片尺寸的关系.

模型将碎片空间分布按季度存储为单独的文件，随着数据积累就形成了一个时间序列.因此，通过分析碎片历史数据的时间变化规律，可以分析碎片的时间演化特征.除阻力消减外，由于碎片发射频率、在轨分裂与碰撞、人工缓解等因素的精确建模都很困难且严重依赖于数据积累，因此这里不考虑碎片演化的物理因素，直接采用时间序列方法分析历史数据的变化规律，并据此进行碎片演化预报.以空间密度为例，若在无碎片骤变的平稳段落，采用AR模型拟合与预报，计算公式为

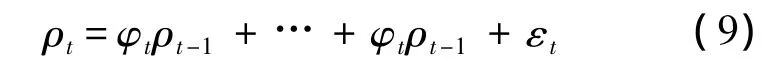
其中，ε是噪声序列;模型系数φ在拟合阶段通过Yule-Walker方程求解.若存在碎片解体等突发事件时，考虑非平稳的时间序列分析方法［13］.

目前主要给出两类预报结果:一是高度层内空间碎片的分布，二是航天器轨道内平均流量，它们均以季度为时间粒度.当然，根据研究需要，也可利用驻留时间比文件进行其他参数的统计、拟合和预报分析，这将在以后研究中予以补充.

3 基于TLE的建模实例

前述的统计建模过程需要输入碎片的轨道数据，并不严格限制数据来源，所用处理方法有一定通用性.本节进行模型实例化与分析，数据来源是北美防空司令部利用美国空间监视网发布的TLE数据库，这是目前可公开获得的最完整且更新性最好的空间碎片数据源［1，7］.对其他编目数据可类似处理.

目前，TLE数据可提供10cm以上和部分1 cm以上的空间碎片编目数据，基本保证1～2 d更新一次，且提供了比较精确的轨道预报模型［14-15］.为了节省计算时间，采用120 s的采样间隔，对每个碎片根据其轨道高度情况分别用 SDP4和SGP4模型［14］预报各编目数据更新周期(通常为1 d)内的轨道，并转化为轨道高度、纬度和经度，进而采用前述的方法和流程进行碎片环境统计建模.以下简称获得的模型为驻留时间统计模型(RTS，Residential Time Statistical model).

ORDEM2000模型可以按年度和尺度给出碎片的空间密度分布，其中大于10 cm的碎片与TLE有类似的测量数据来源，因此，将RTS与其进行对比验证.

图2给出了2011年和2014年碎片空间密度的计算结果，可见ORDEM2000与RTS的曲线变化趋势基本一致，即碎片空间密度均随高度降低而减小，这种现象的一个重要原因是低轨大气阻力加大导致碎片快速下降所致.RTS曲线相对平滑，这是由于其采用三次多项式插值而ORDEM2000采用线性插值所致.此外，RTS的密度幅度略高.这是因为此处的ORDEM2000仅统计了10 cm以上的碎片且数据时间较早，而RTS所用新的TLE数据包含了10 cm以下碎片.

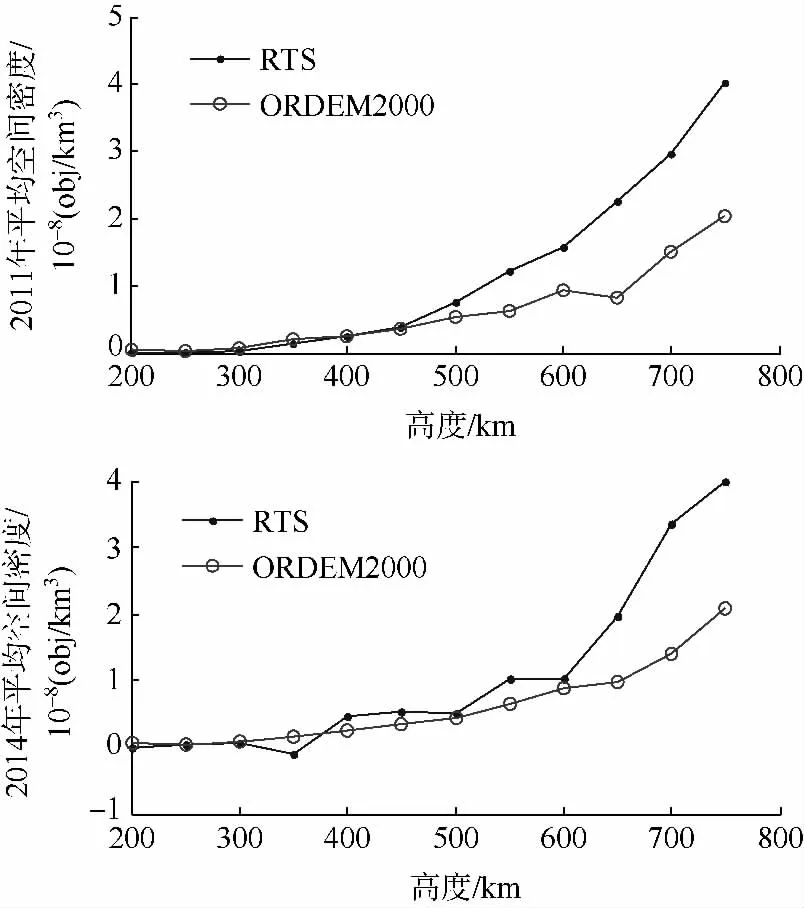
图2 本文模型(RTS)与ORDEM2000模型的空间密度对比Fig.2 Space debris density according to RTS and ORDEM2000

图3 驻留时间比的经纬度分布情况Fig.3 Geodetic distribution of the residual time ration

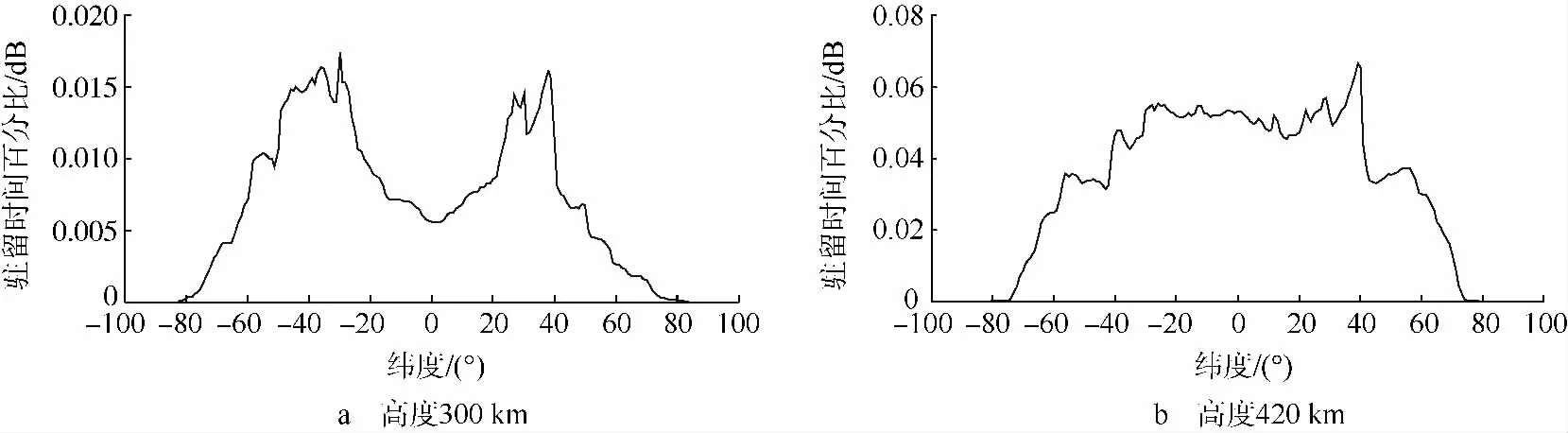
图4 驻留时间比的纬度分布情况Fig.4 Latitude distribution of the residual time ration

图3是2010年第一季度300km和420km高度层的碎片驻留时间比(以dB形式给出以便于显示)，图4则给出了它们在纬度带内的分布情况.可见纬度分布上存在分布峰值，且两极地区碎片密度较少;420 km的碎片密度明显多于300 km;300 km的碎片分布在个别轨道上比较密集，而420 km的碎片在经度分布上则已比较均匀.进一步，通过综合分析其他年度不同高度层碎片分布情况，表明:低轨碎片纬度分布主要集中在-60°～60°之间，基本上呈现南北对称特性，但有一定的分布差异，其中20°，40°和60°纬度带在一些高度层，特别是400～700 km高度，出现了局部分布密度较大的带状峰值;350 km高度以下碎片的经度分布有一定的不均匀性，但随着高度增加碎片在经度上分布趋于均匀.

图5是碎片空间密度随时间的变化曲线，可见各高度层内的碎片空间密度相对比较稳定，这些结论与ORDEM和MASTER等一些公开模型的分析结果是基本一致的［4-7］.

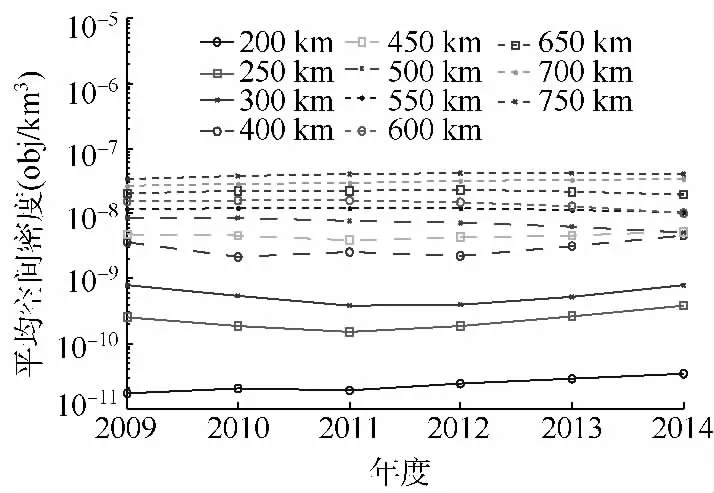
图5 碎片空间密度随时间的变化情况Fig.5 Space debris density changes with time

4 结论

低地轨道空间碎片的增多已经严重影响了航天器的正常工作和安全飞行，因此，建立空间环境模型以评估航天器在轨运行的碰撞风险是十分必要和迫切的.本文借鉴国内外空间碎片环境工程模式的建模思想，综合利用轨道预报和多项式拟合及求根方法，进行了空间碎片分布统计，并在此基础上给出了基于多项式插值和时间序列分析的碎片环境模型描述方法，该建模方法可以适用于各种编目轨道数据.以TLE数据为例进行了模型验证和空间碎片分布规律的研究，获得了与ORDEM2000模型类似但尺度更加细致的计算结果.文中所述碎片环境建模方法和分析结论可为低轨道航天器，特别是近地载人航天器的碰撞风险评估和防护设计等工作提供参考.后续工作将集中于模型长时间预报性能的改进，以及模型在航天器轨道设计和碰撞规避能力设计等工作中的具体应用.

References)

［1］王海福，冯顺山，刘有英.空间碎片导论［M］.北京:科学出版社，2010 Wang Haifu，Feng Shunshan，Liu Youying.Introduction of space debris［M］.Beijing:Science Press，2010(in Chinese)

［2］ Johnson N L.History of on-orbit satellite fragmentations［R］.NASA/TM-2008-214779，2008

［3］彭科科.空间碎片环境探测数据处理方法及工程模型建模方法研究［D］.哈尔滨:哈尔滨工业大学，2010 Peng Keke.Research on sapce debris environment exploration data processing measure and engineering modeling method［D］.Harbin:Harbin Institute of Technology，2010(in Chinese)

［4］张平平.近地轨道空间碎片轨道参数分布规律研究［D］.哈尔滨:哈尔滨工业大学，2006 Zhang Pingping.Research on space debris orbital parameter distribution uule in LEO［D］.Harbin:Harbin Institute of Technology，2006(in Chinese)

［5］唐颀，庞宝君，张伟.空间碎片环境工程模式参数分析［J］.中国空间科学技术，2004，24(5):22-27 Tang Qi，Pang Baojun，Zhang Wei.Analysis of the parameters in space debris environment engineering model［J］.Chinese Space Science and Technology，2004，24(5):22-27(in Chinese)

［6］ Fukushige S，Akahoshi Y，Kitazawa Y.Comparison of debris environment models:ORDEM2000，MASTER2001 and MASTER2005［J］.IHI Engineering Review，2007，40(1):31-41

［7］ Liou J C.The new NASA orbital debris engineering model［R］.ORDEM2000，NASA/TP-2002-210780，2002

［8］ Liou J C.NASA's ORDEM2010 status［C］//28th Inter-agency Debris Coordination Committee Meeting(IADC).Trivandrum，India:NASA，2010:1-20

［9］王海福，余庆波，刘有英.空间碎片碰撞风险评估系统［J］.北京理工大学学报，2008，28(12):1039-1042 Wang Haifu，Yu Qingbo，Liu Youying.Orbital debris risk assessment system［J］.Transactions of Beijing Institute of Technology，2008，28(12):1039-1042(in Chinese)

［10］ Xu X L，Xiong Y Q.A research on the collision probability calculation of space debris for nonlinear relative motions［J］.Chinese Astronomy and Astrophysics，2011(35):304-317

［11］《数学手册》编写组.数学手册［M］.北京:高等教育出版社，2010:87-89“Handbook of Mathematics”Writing Group.Handbook of mathematics［M］.Beijing:Higher Education Press，2010:87-89(in Chinese)

［12］ Klinkrad H.Space debris-models and risk analysis［M］.New York:Springer＆ Praxis，2006

［13］王正明，易东云.测量数据建模与参数估计［M］.长沙:国防科技大学出版社，1996 Wang Zhengming，Yi Dongyun.Instrumental data modeling and parameter estimation［M］.Changsha:University of National Defence Technology Press，1996(in Chinese)

［14］ Felix R，Ronald L.Space track report No.3:models for propagation of NORAD element sets［R］.Peterson:Aerospace Defense Command，United States Air Force，1980

［15］ Levit C，Marshall W.Improved orbit predictions using two-line elements［J］.Advances in Space Research，2011，47(7):1107-1115