半月板光放大性
袁 玫,李金环
(东北师范大学 物理学院,吉林 长春130024)
1 引 言
在古希腊,“弯月”代表的是在两竖直固体表面间附着的液体膜所构成的形状.2013年全国大学生物理学术竞赛中有一个问题是:在不透明的薄材料上剪一狭缝,将薄材料浸没在水中,然后将薄材料从液体中移出,可以从狭缝中看见液体的薄膜,照亮狭缝.研究产生图样的成因.本文中只研究塑料材质水平放置的狭缝所产生的放大图像,实验光路图见图1.

图1 实验光路图
2 理论分析
2.1 弯液面形状

水平方向受力平衡:

所以

由数学几何关系知:


图2 受力分析
由(6)~(8)式得,z″(y)>0,Δz′(y)<0.因此,水平狭缝中的水膜成凹液面,下半段呈下降趋势,与下半段凹液面曲线完全相同[3].
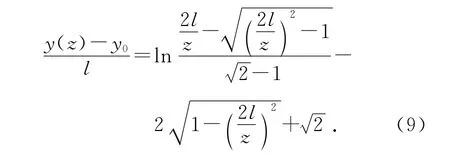
2.2 弯液面与凹透镜等效条件
弯液面与凹透镜等效条件见表1.

表1 弯液面等效凹透镜条件
2.3 带有水狭缝焦距计算公式
焦距计算示意图如图3所示,根据相似三角形原理可知:

则有水狭缝焦距为


图3 焦距计算示意图
3 实验探究
为了研究半月板的光放大性,实验中使用He-Ne激光器产生的最大波长为632.8nm,所以将夹缝宽度控制在1~3mm,使波长与缝宽不在同一数量级,即不会出现单缝衍射现象.
3.1 验证半月板成像的凹透镜放大性
控制狭缝、像屏位置均不变,在狭缝中有液体薄膜和无液体薄膜,有10cm焦距凹透镜的3种情况下进行实验,图4为观察光屏上的图像.

图4 不同条件实验对比图
在有水狭缝条件下,将一纸屏从紧靠狭缝向远离狭缝移动,观察发现条纹逐渐增大,且始终比光源大.
实验证明:有水狭缝始终对光斑成放大作用,且放大性与凹透镜类似.
3.2 研究半月板光学性质与狭缝厚度t关系
狭缝被水充满时,固定狭缝和光屏情况下,s′=27.1cm,b=0.2cm,改变不同的狭缝厚度t,读取d,计算f变化,每个狭缝厚度做7组实验.
每个狭缝厚度取7组实验的最大值,拟合得:f=-1.256t+12.18,R2=0.982.图5中,相同狭缝厚度的不同数据点,表示液体体积不同.由图5中总体趋势可看出:随着狭缝厚度t的增加,图像的焦距以一次函数的趋势逐渐减小,与理论所推得的公式f=-相符.

图5 f-t关系
水膜位置对图像的影响如图6所示,当狭缝厚度不断增加时,狭缝间可填充水的最大体积增加,即填充水的体积范围扩大.填充水体积小时,狭缝主要起到的是光阑作用;填充水体积最大时,狭缝主要起到的是光学透镜作用;填充水体积位于中间范围时,狭缝主要起到的是光阑与透镜的共同作用.由于每次不能保证填充水的体积一定,故狭缝厚度越大,每次填充的水体积差异也越大,误差越大.多次实验的目的是为了尽可能的保证狭缝间水的体积最大,光学性质最好.

图6 水膜位置对图像的影响
当狭缝厚度足够大,水不能充满狭缝时,狭缝起到光阑的作用.水膜靠近光屏时,有较多光线通过;水膜远离光屏时,透过光线较少.
3.3 研究半月板光学性质与狭缝宽度b关系
固定狭缝和光屏情况下,s′=27.1cm,改变不同的狭缝宽度b,读取d,计算f的变化,每个狭缝宽度做3组实验.

图7 f-b关系
图7中,相同狭缝宽度b的不同数据点,表示液体体积不同.选取图7中放大程度最大的一组数据,由于填充水最接近最大体积,故误差最小,可看出:随着单缝宽度b的增大,焦距f先增大再减小,由理论值:
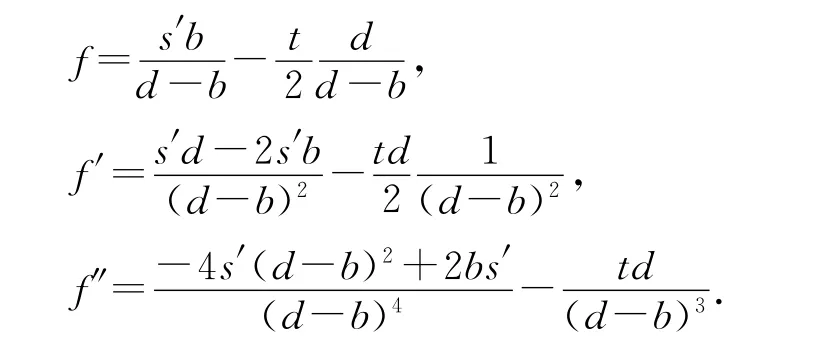
因为d≫b,所以4(d-b)2≈4d2>2b,所以f″<0,即曲线向下凹,实验与理论相符.
由图7中可看出,第2,3组数据中虽然填充水不是最大体积,即狭缝包括透镜和光阑两方面作用,但此时仍然以水的透镜作用为主,与理想情况下焦距变化的趋势相同.
3.4 研究半月板光学性质与狭缝倾角φ的关系
固定狭缝和光屏位置情况下,s′=27.1cm,t=1mm,改变狭缝的位置与水平方向的夹角φ,根据图像的弯曲程度,粗略测量图像的曲率,得到的R-φ图像如图8所示.

图8 R-φ关系
由图8总体趋势可看出:随着狭缝角度φ的增大,图像曲率逐渐增大.
4 结 论
本文研究了狭缝水膜的形状,以及它的光学放大性质.实验结果表明,水膜呈二次函数的凹液面,光学放大性质与凹透镜有着相同的性质.随着狭缝厚度t的增加,水膜焦距呈线性下降趋势;单缝焦距也与狭缝宽度b呈二次函数关系;随着狭缝角度的增加,图像曲率也在不断增加.
[1]周述苍,郭天葵,周莹.基于LabVIEW的液体表面张力系数测定[J].物理实验,2012,32(12):30-32.
[2]Biery J C,Oblak J M.Calculational method for determination of surface tensions from photographed menisci[J].I & EC Fundamentals,1966,5(1):121-128.
[3]Deserno M M.The shape of a straight fluid meniscus[Z].2004-03-15.

