TC4-DT合金的超塑性变形及其本构方程
郑漫庆,王高潮,徐雪峰,喻淼真
(南昌航空大学 航空制造工程学院,南昌330063)
国际航空结构材料的设计概念正由单纯静强度设计向现代的损伤容限设计准则转变[1],要求钛合金在具有一定强度水平条件下,同时具有高的断裂韧性和低的裂纹扩展速率[2,3],这对钛合金提出了更高的要求,从而影响了钛合金的热加工工艺方向[4,5]。作为一种新型的损伤容限型钛合金,TC4-DT合金因其优异的综合力学性能主要应用于飞机承力构件上。研究TC4-DT合金的超塑性变形过程中的动态再结晶行为以及本构关系,可以准确描述TC4-DT合金的流变行为,为该合金超塑成形工艺过程设计和数值模拟分析提供基础数据。
本工作采用恒应变速率拉伸方法对TC4-DT合金的动态再结晶进行研究,这是因为金属材料热变形时所发生的组织演变决定其成形后的性能,其中,一种重要的组织演变机制是动态再结晶。随着计算机技术的发展,可通过有限元模拟技术模拟材料在热变形过程中的微观组织演变,以达到预测与控制材料组织的目的[6]。采用有限元软件模拟材料热变形组织演变的必要条件之一是建立动态再结晶动力学模型,从而为科学地制定TC4-DT合金热加工工艺提供理论依据。材料本构关系不仅可以通过经典数学模型来建立[7,8],也可以通过回归软件来直接建立,如著名的Origin,SPSS,Matlab及国产的1stopt软件,但无论是通过经典数学模型还是直接利用回归软件建立本构关系,都存在精度问题,而要对变形过程做到精确控制,就必须要求所建立的本构模型具有足够的精度,而精度问题在构建本构方程时不是一次就能保证的,往往需要通过若干次的修正来保证,因此本工作在建立本构方程的基础上对其进行了修正。
1 实验材料与方法
实验用材料为TC4-DT钛合金,对其进行能谱测试,精确测定其成分(原子分数)为:Ti 90.09%,Al 5.56%,V 4.34%。合金原始晶粒尺寸约为15μm,组织为初生α相和转变β相且分布较为均匀[9,10]。
本实验使用CMT4104电子万能拉伸试验机进行超塑性拉伸实验。将TC4-DT合金棒材加工成如图1所示的拉伸试样,变形区域应无裂纹、划痕等可能影响实验结果的缺陷。
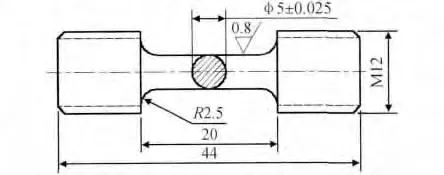
图1 TC4-DT合金超塑性拉伸试样尺寸Fig.1 The superplastic tensile sample dimension of TC4-DT alloy
恒应变速率超塑性拉伸实验:在870℃下,应变速率为3.3×10-4s-1。
应变速率循环超塑性拉伸实验:在850~890℃下,应变速率循环范围为3.3×10-5~3.3×10-3s-1。
2 动态再结晶动力学模型
恒应变速率法的应力-应变曲线如图2所示,表现为三个阶段:初始阶段为加工硬化阶段;当应变超过临界应变时,材料开始出现动态再结晶,硬化率下降;当动态再结晶造成的软化与应变硬化达到动态平衡时,进入稳定再结晶阶段,流变应力趋于恒定[11,12]。

图2 恒应变速率法的应力-应变曲线Fig.2 Stress-strain curve of the constant strain rate method
本工作采用经典的Avrami方程来描述TC4-DT合金的动态再结晶动力学模型[13],动态再结晶的体积分数Xd与应变ε之间的关系可以表示为:

式中:εc为发生再结晶的临界应变;εp为发生再结晶的峰值应变;βd,kd均为与材料有关的系数。
根据应力-应变曲线来确定Xd:

式中:σde为动态回复过程中的瞬态应力;σdes为动态回复过程中的稳态应力;σdx为动态再结晶过程中的瞬态应力;σdxs为动态再结晶过程中的稳态应力。
采用峰值应力近似地代替σde和σdes,则式(3)可表示为:

由式(1)推导可得:
通过绘制ln[-ln(1-Xd)]与ln[(ε-εc)/εp]的曲线,并利用Origin软件进行拟合,便可求得kd与lnβd的值,如图3所示。


图3 ln[-ln(1 -Xd )]与ln[(ε-εc )/εp]的关系曲线Fig.3 The curve of ln[-ln(1 -Xd)]and ln[(ε-εc)/εp]
由图3拟合出的公式为:Y=A+BX,其中:A=-2.60208,B=1.42114,该公式的精度R=0.98137。计算 得:kd=1.42114,βd=exp(-2.60208)=0.07412。
所以该动态再结晶动力学方程为:
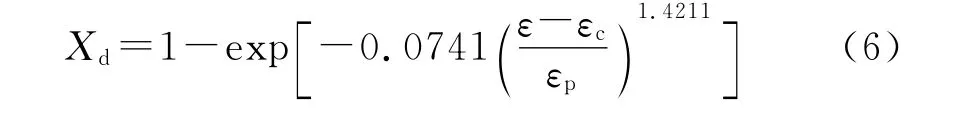
3 本构模型的建立与修正
3.1 Arrhenius型方程的建立与检验
反映材料动态特性的本构关系可能因为材料的不同而存在较大的差异,即使是同一种材料,也可能因为不同的目的不同的需求而建立不同形式的本构关系。常用Arrhenius型方程一般有三种形式:

根据Arrhenius型方程中流动应力的表现形式,式(7)~(9)分别称为指数方程、幂函数方程与双曲正弦方程。其中:Q为变形激活能(J/mol);R为气体常数(J/(mol·K));T为绝对温度(K);A1,A2,A3和α为常数;β,n1,n为与应变速率敏感性因子有关的参数。
由式(7)~(9)两边取自然对数,然后整理可得统一形式:

式中:f(σ)可分别表示σ,ln(σ)和ln[sinh(ασ)]。通过对实验数据的计算[14,15]可最后求得不同温度下的β与n1及计算所得的α值如表1所示。

表1 不同温度下的β,n1与α值Table1 The values ofβ,n1andαat different temperatures
由表1数据可得α的平均值为0.019570MPa-1。
应用双曲正弦型Arrhenius方程对TC4-DT合金进行适用性分析时,均采用α的平均值进行计算。由Arrhenius双曲正弦型方程可推导出变形激活能的表达式为:


通过计算可求得各温度下的n,k值及lnA值如表2所示。由表2计算激活能Q=Rnk=171.9kJ/mol。
由式(9)可得:


表2 各温度下的n,k值及计算所得的lnA值Table2 The values of n,kand lnAat different temperatures
代入表2相关的值可得TC4-DT合金在两相区超塑性拉伸的本构方程为:
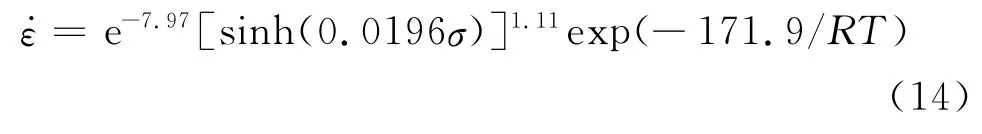

通过计算,在用于构建本构方程的实验数据点中,误差小于15%的实验数据点占总数据点的74%,误差小于10%的实验数据点占总数据点的51%。图4为所构建本构方程的误差精度效果图,图4中两条直线组成的楔形带为满足相对误差小于和等于15%的误差带,中间一条直线上的点是实验值与计算值相等的点。从图4可以看出,相当一部分点落在15%的误差带外。

图4 计算应力与实验应力分散图Fig.4 The scatter diagram of calculated stress and experimental stress
以上分析表明,所构建本构方程的精度不足,需对现有的本构方程加以修正。
3.2 本构模型的修正与检验
以上述本构方程求得的σcalc及温度T为自变量,以σexp为因变量,可借助国产1stopt软件进行二元非线性回归,获得的数据拟合结果如图5所示。
图5(a)为利用1stopt软件进行二元非线性回归拟合后的X-Y散点图,各点与对角线的垂直距离表示修正后的误差,即σcor与σexp的偏差,落在对角线上的点表示σcor与σexp相等的点。图5(b)为利用1stopt软件进行二元非线性回归拟合后的双线图,其中,蓝色曲线表示σexp曲线,红色曲线表示σcor曲线,红色曲线与蓝色曲线的偏差即表示σcor与σexp的偏差。
拟合出的方程如式(16)所示,精度R2=0.9990。

图5 应变速率循环实验数据的拟合图形(a)X-Y散点图;(b)双线图Fig.5 The experimental data fitting graphs(a)X-Yscatter plot;(b)double figure
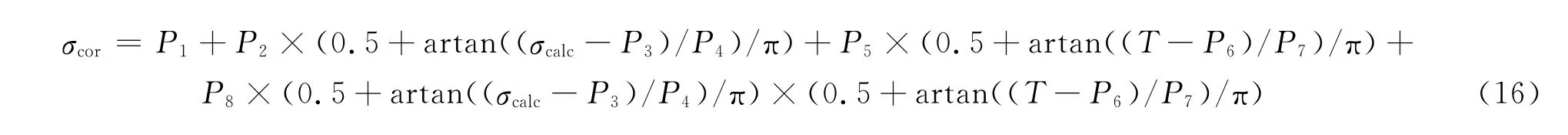
其中:σcalc=arsinh[(ε·exp(171.9/RT +7.97))1/1.11]/0.0196。
所得的回归系数见表3。

表3 修正后方程的回归系数Table3 The regression coefficient of corrected equation
通过计算,在用于构建本构方程的实验数据点中,误差小于15%的实验数据点占总数据点的99.8%,误差小于10%的实验数据点占总数据点的95.5%。图6为修正本构方程后的误差精度效果图,图中两条直线组成的楔形带为满足相对误差小于和等于15%的误差带,中间一条直线上的点是实验值与计算值相等的点。从图6可以看出,几乎所有点落在15%的误差带内。以上检验表明,所构建的本构方程的精度较高。
图7为不同温度下所构建的本构方程求出的流动应力计算值与实验值的比较图。可以看出根据所构建的本构方程计算所得的流动应力值与实验数据吻合程度较好。
以上的误差分析表明,构建的TC4-DT合金的本构方程有较高的精度,且具有普遍适用性,可用于实际热加工过程的变形抗力计算,也可作为有限元模拟的本构方程。

图6 修正后计算应力与实验应力散点图Fig.6 The scatter diagram of calculated stress and the experimental stress after correction
4 结论
(1)在超塑性变形过程中存在动态回复与动态再结晶现象,采用Avrami方程描述了动态再结晶动力学行为,在870℃,应变速率为3.3×10-4s-1时合金的再结晶体积分数为:Xd=1-exp[-0.0741

图7 不同温度下流动应力计算值与实验值比较(a)850℃;(b)870℃;(c)890℃Fig.7 The comparison ofσcalcandσexpat different temperatures(a)850℃;(b)870℃;(c)890℃
(2)采用逐步回归、逐步修正的方法,即利用经典模型Arrhenius方程获得了本构关系后,把方程左边的因变量即σcalc作为自变量,再加一个温度T或1/T的调节变量作为自变量,而将实验所得σexp作为因变量,通过1stopt软件在程序中自动查找拟合,可使本构关系得到修正,修正后本构方程的精度可达99.9%。
[1]曹春晓.选材判据的变化与高损伤容限钛合金的发展[J].金属学报,2002,38(增刊):4-11.CAO C X.Change of material selection criterion and development of high damage-tolerant titanium alloy[J].Acta Metallurgica Sinica,2002,38(Suppl):4-11.
[2]SINHA V,SOBOYEJOW W O.An investigation of the effects of colony microstructure on fatigue crack growth in Ti-6Al-4V[J].Materials Science and Engineering:A,2001,319-321:607-612.
[3]李辉,曲恒磊,赵永庆,等.显微组织对Ti-6Al-4VELI合金疲劳裂纹扩展速率的影响[J].稀有金属快报,2006,25(3):26-29.LI H,QU H L,ZHAO Y Q,et al.Effects of microstructure on fatigue crack growth rate of damage tolerance for TC4-DT alloy[J].Rare Metals Letters,2006,25(3):26-29.
[4]SWIFT T.Damage tolerance capability[J].International Journal of Fatigue,1994,16(1):75-96.
[5]ARRIETA A J,STRIZ A G.Optimal design of aircraft structures with damage tolerance requirements[J].Struct Multidisc Optim,2005,30(2):155-163.
[6]陈学海,陈康华,董朋轩,等.7085铝合金的热变形组织演变及动态再结晶模型[J].中国有色金属学报,2013,23(1):44-50.CHEN X H,CHEN K H,DONG P X,et al.Microstructure evolution and dynamic recrystallization model of 7085aluminum alloy during hot deformation[J].The Chinese Journal of Nonferrous Metals,2013,23(1):44-50.
[7]YANG J H,LIU Q Y,SUN D B,et al.Recrystallization behavior of deformed austenite in high strength microalloyed pipeline steel[J].Journal of Iron and Steel Research,International,2009,16(1):75-80.
[8]王智祥,刘雪峰,谢建新.AZ91镁合金高温变形本构关系[J].金属学报,2008,44(11):1378-1383.WANG Z X,LIU X F,XIE J X.Constitutive relationship of hot deformation of AZ91magnesium alloy[J].Acta Metallurgica Sinica,2008,44(11):1378-1383.
[9]喻淼真,王高潮,郑漫庆,等.TC4-DT合金应变诱发最大m值超塑性变形研究[J].航空材料学报,2014,34(3):15-20.YU M Z,WANG G C,ZHENG M Q,et al.Superplastic deformation based on strain-induced and maximal mvalue in TC4-DT titanium alloy[J].Journal of Aeronautical Materials,2014,34(3):15-20.
[10]喻淼真,王高潮,郑漫庆,等.TC4-DT合金改锻工艺及超塑性变形行为[J].塑性工程学报,2013,20(5):1-6.YU M Z,WANG G C,ZHENG M Q,et al.Forging pretreatment process and superplastic deformation behavior of TC4-DT alloy[J].Journal of Plasticity Engineering,2013,20(5):1-6.
[11]张庭芳.镁合金板料热拉深成形实验与数值模拟研究[D].南昌:南昌大学,2008.ZHANG T F.Study on experiment and numerical simulation of magnesium alloy sheet metal warm deep drawing[D].Nanchang:Nanchang University,2008.
[12]刘智恩.材料科学基础[M].西安:西北工业大学出版社,2008.273-274.LIU Z E.Material Science[M].Xi’an:Northwestern Polytechnical University Press,2008.273-274.
[13]LIN Y C,CHEN M S.Numerical simulation and experimental verification of microstructure evolution in a three-dimensional hot upsetting process[J].Journal of Materials Processing Technology,2009,209(9):4578-4583.
[14]范定兵,王高潮,赵晓宾.Ti-15-3超塑性研究[J].南昌航空工业学院学报:自然科学版,2007,21(1):26-29.FAN D B,WANG G C,ZHAO X B.Research on superplasticity of Ti-15-3titanium alloy[J].Journal of Nanchang Institute of Aeronautical Technology:Natural Science Edition,2007,21(1):26-29.
[15]耿启东,王高潮,董洪波.TA15合金应变速率循环超塑性研究[J].热加工工艺,2008,37(11):43-48.GENG Q D,WANG G C,DONG H B.Superplasticity of TA15 titanium alloy induced by strain rate cycling[J].Hot Working Technology,2008,37(11):43-48.

