三频载波多普勒组合的北斗星载钟短稳评估方法

龚航，张鑫，黄新明，朱祥维，王飞雪

(国防科技大学 电子科学与工程学院，湖南 长沙，410073)

卫星导航系统中星载钟频率稳定度的在轨特性对于卫星钟完好性监测具有重要意义。对于卫星钟差建模、仿真及预报等应用，需要获取准确的卫星钟短期稳定度参数。通常对GPS卫星钟稳定度的评估方法是利用IGS的精密钟差产品[1−2]，由于北斗系统(BeiDou navigation satellite system，BDS)目前尚无公开的精密钟差产品，该方法目前仅限于GPS和GLONASS系统，并不适用于北斗系统。另一方面，解算卫星钟差通常采用的精密定轨与时间同步方法(ODTS法)需要大型地面监测网的连续观测和复杂的钟差确定算法[3−4]，一般的北斗用户无法获取监测网数据，并且算法实现较为复杂。Gonzalez等[5−8]对几种单站评估方法进行分析比较，其中基于精密星历的方法并不适用于现阶段的北斗系统[5]，基于载波相位拟合的方法结果过于乐观[6]，基于平滑广播星历的方法(SBE法)对载波周跳较为敏感[7]，基于星地双向比对的方法不适用于普通用户(一般用户无法获取星地双向比对的数据)[8]。本文作者针对北斗系统的特点，提出一种基于单站三频载波多普勒组合观测量的星载钟短稳评估方法，以较简单的方法实现与复杂算法相当的评估精度。

1 方法原理

1.1 载波多普勒评估方法原理

设GNSS卫星发射的下行导航信号为：

其中：a1为发射信号幅度；x(t)为调制的扩频码；fi为标称下行发射载波频率；Δfs为星载钟基准信号f0(如10.23 MHz)的频偏；bi为载波标称频率与基准频率的比例系数(bi=fi/f0)；θi为初相。由于数据调制对测距不会造成影响，式(1)中没有考虑在信号中调制的数据。

这样，接收机收到的下行信号为[9]

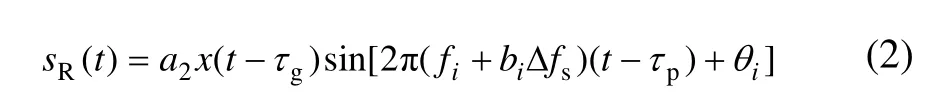
其中：a2为接收信号幅度；τg为扩频码传播延迟(群延迟)；τp为载波传播延迟(相延迟)。

接收机在收到sR(t)后，先将其下变频为中频信号，再进行载波跟踪和伪码相关等处理。经过射频前端处理后的中频信号为

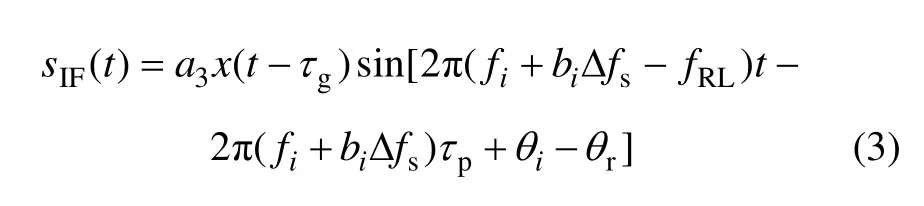
其中：fRL为接收机将fi下变频为中频fIF时的本振频率，θr为该本振的初相，由于

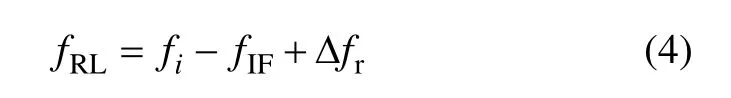
接收机接收到的中频信号为

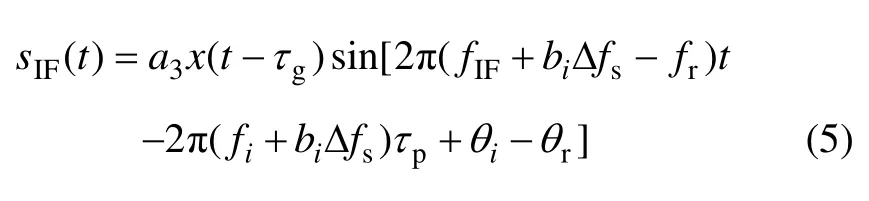
其中：∆fr为接收机下变频时的本振频偏。载波多普勒测量值为实际接收信号的载波频率与标称频率的差，即接收机本地复制中频载波信号的频率减去标称中频频率，于是，t时刻接收机载波多普勒测量值fdi为

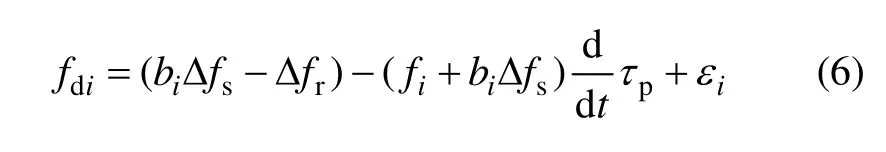
其中：εi为载波多普勒的观测噪声，并且

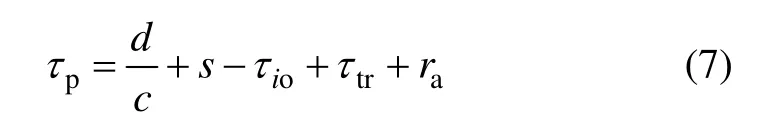
d为卫星与接收机的星地几何距离；c为光速；s为Sagnac效应引入的时延；τio和τtr分别为电离层和对流层引入的传播延迟；ra为相对论效应产生的卫星钟差。于是，有

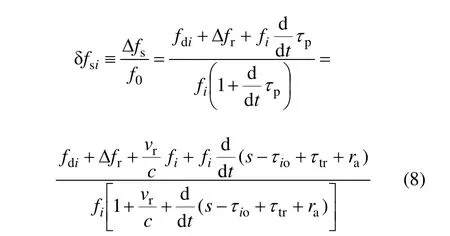
由式(8)可知：利用载波多普勒观测值fdi可计算出星载钟的相对频差δfsi，但是，需要首先对观测值中包含的s，τio，τtr和ra等误差进行修正。

式(8)中，vr为卫星与接收机的相对运动速度，在接收机坐标已知的情况下可利用卫星星历计算获得；s和τtr可利用模型进行修正；τio可通过多频组合修正；ra可通过下式进行修正[10]：

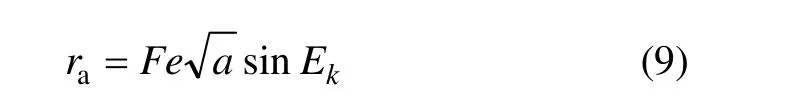
其中：F=−4.442 807 633×10−10s/m1/2；e为卫星轨道偏心率；a为卫星轨道半长轴；Ek为卫星轨道偏近点角。

在完成上述修正后，对于单站评估方法，若令∆fr为常数，即获得以接收机时钟为基准的卫星钟相对频偏。若接收机采用高性能原子钟作为参考基准，由于地面钟的稳定度可比星载钟高 1个数量级以上，∆fr的抖动对δfsi的影响可以忽略，利用下式即可实现对星载钟的稳定度进行评估[11]：

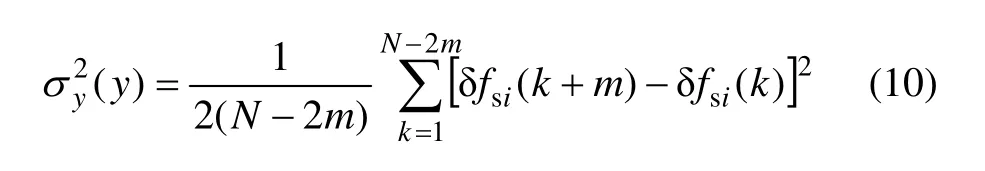
由上述实现原理可知：由于该方法输入的观测量是载波多普勒，实际上是一种频率测量方法，因此，不需要对载波周跳进行探测与修复处理。当出现载波周

跳时，载波多普勒测量值可能出现野值，导致估算的δfsi存在野值，这时，只需在利用式(10)计算频率稳定度时进行野值剔除处理[12]，相比SBE法较容易实现。

1.2 三频多普勒组合修正电离层误差

式(8)包含的各种误差中，电离层延迟τio的影响最大，并且由式(6)~(7)可知，三频载波多普勒观测数据的主要区别在于电离层延迟不同。对于各GNSS系统使用的L频段而言，1 d的电离层延迟波动幅度可达几十ns，若不能准确地将其修正，则修正残差会显著增加较长平滑间隔频率稳定度的估计误差。相比模型和格网等修正方法，双频或多频组合是更为有效的方法。随着GPS和Galileo、北斗等卫星导航系统向三频系统的发展，可利用三频观测组合实现更准确的电离层延迟误差修正[13−14]。但是，三频组合会放大噪声方差，导致较短平滑间隔频率稳定度的估计误差增大，因此，必须选择噪声方差放大倍数较小的组合量，最常用的为三频一阶组合[14]。以下推导载波多普勒三频一阶无电离层组合的表达式。

采用电离层一阶模型，将式(6)改写为与电离层相关和无关的2部分：

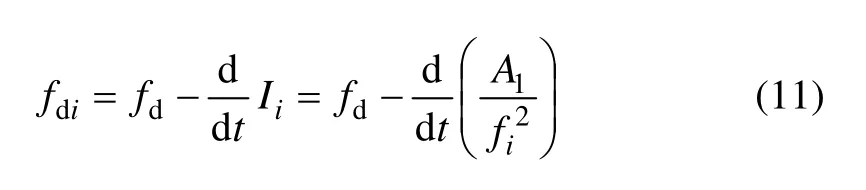
其中：

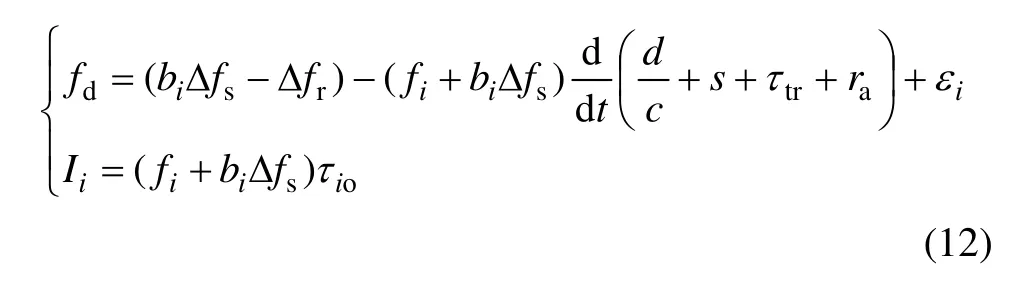
将载波多普勒观测的无电离层组合记为

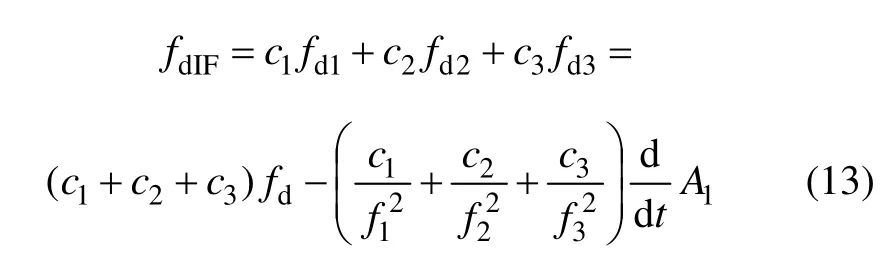
三频一阶无电离层组合系数满足：

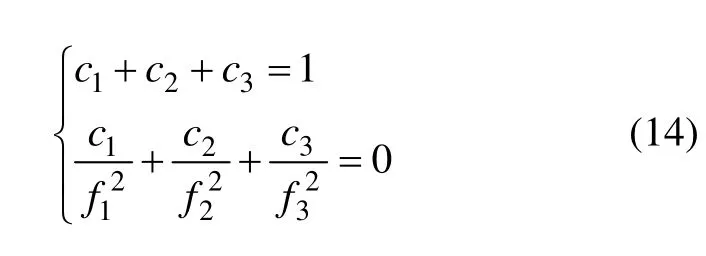
假定三频载波多普勒观测具有相同的噪声方差σε2，fdIF的噪声方差为

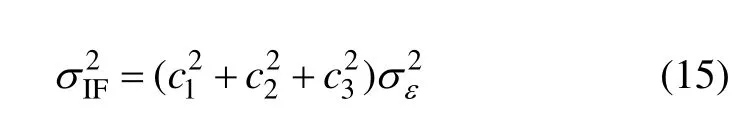
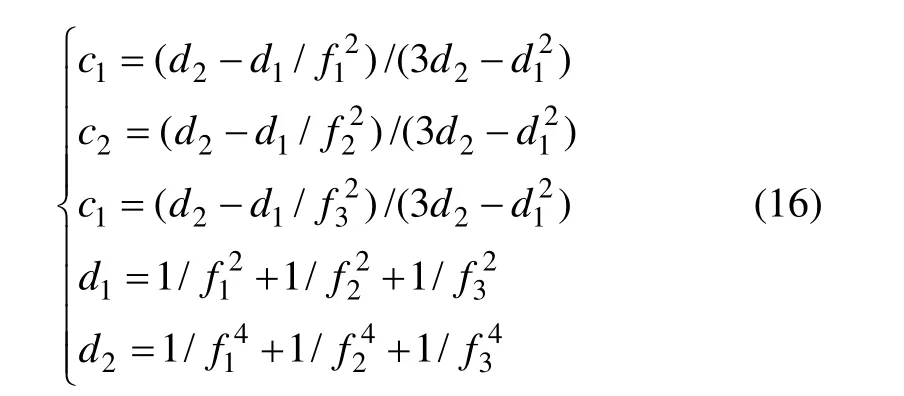
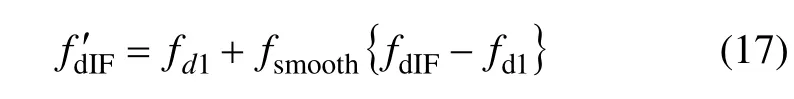
其中：fsmooth{·}为平滑运算函数。

由式(17)可知：通过对三频组合修正量的平滑处理可以获得与单频观测相同的噪声方差[10]，使电离层延迟修正对较短和较长平滑间隔的稳定度评估引入的误差都降到最低。

2 方法实现流程

以上讨论利用三频载波多普勒组合评估星载原子钟短期稳定度方法的原理，该方法记为TFCD法(Triple-Frequency Carrier Doppler Combination Method)。其实现流程如图1所示。

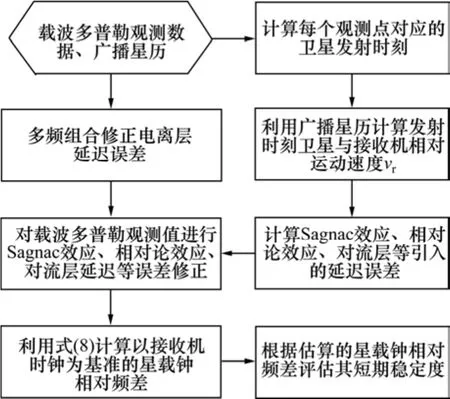
图1 TFCD法实现流程Fig. 1 Flow chart of TFCD method

3 方法性能验证实验

由于目前无法获取北斗的精密钟差作为验证手段，除文献[16]给出利用 ODTS方法获得的 2012−02部分卫星的100～100 000 s的稳定度结果外，目前尚无公开发表的北斗星载钟短稳结果。本文作者基于北斗系统相距约3 000 km的01和03号2个监测站同一时段的观测数据利用 TFCD法进行星载钟短稳评估实验，对 2个站的结果进行相互验核，同时将文献[16]给出的结果作为对比参考。这2个站的接收机均采用氢钟作为参考，接收机时钟的稳定度优于星载钟，满足单站评估条件。

实验选择的观测时段为北斗时 2012−12−03T 00:00:00 至2012−12−04T 00:00:00(无法获得与文献[16]同时期的观测数据)，利用B1，B2和B3共3个频点的载波多普勒观测数据对卫星 SV10的星载钟(铷钟)的短稳进行评估，结果如图2所示。

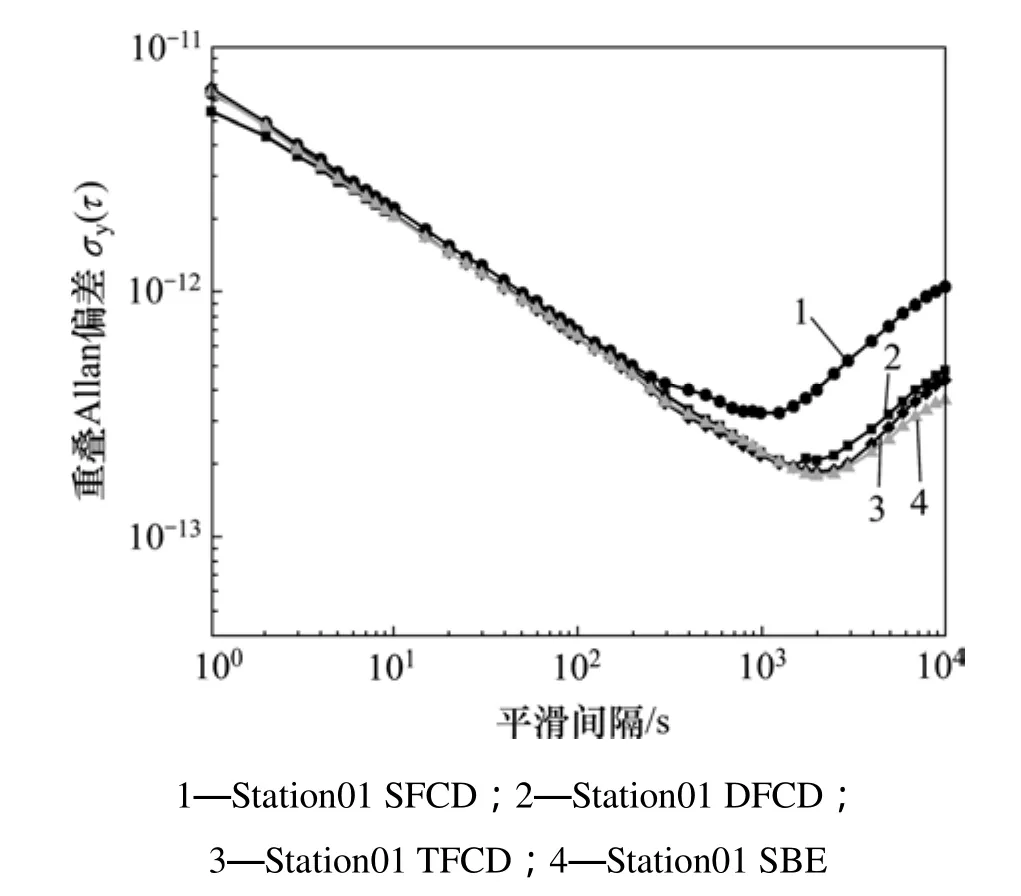
图2 01站的4种方法结果比较Fig. 2 Results comparison of four methods for station01

图2 中Station01 SFCD为通过本文方法基于B1单频载波多普勒观测值的评估结果，其中电离层延迟采用Klobuchar模型修正方法；Station01 TFCD为通过本文方法利用式(17)三频修正方法的结果；Station01 DFCD法为双频修正方法的结果；“Station01 SBE法”为利用SBE法的计算结果[7]，电离层延迟采用三频一阶修正方法。由图2可见：双频及三频组合均有效地修正了电离层延迟修正残差的影响，在平滑间隔300 s以上明显好于单频结果，并且由于平滑处理使得平滑间隔较小的短稳结果没有被恶化。由于北斗系统B2、B3频点较为接近，三频组合结果虽然略好于双频结果，但是基本一致。另外，利用本文方法获得的结果与SBE法一致，10 000 s平滑间隔内的相对误差小于10%。

利用监测站01、03同一时段的载波多普勒观测数据对 SV10星载钟短稳的评估结果如图 3所示(文献[16]的结果扣除卫星钟的频漂，为与其比较，图 3的结果中扣除频漂)。

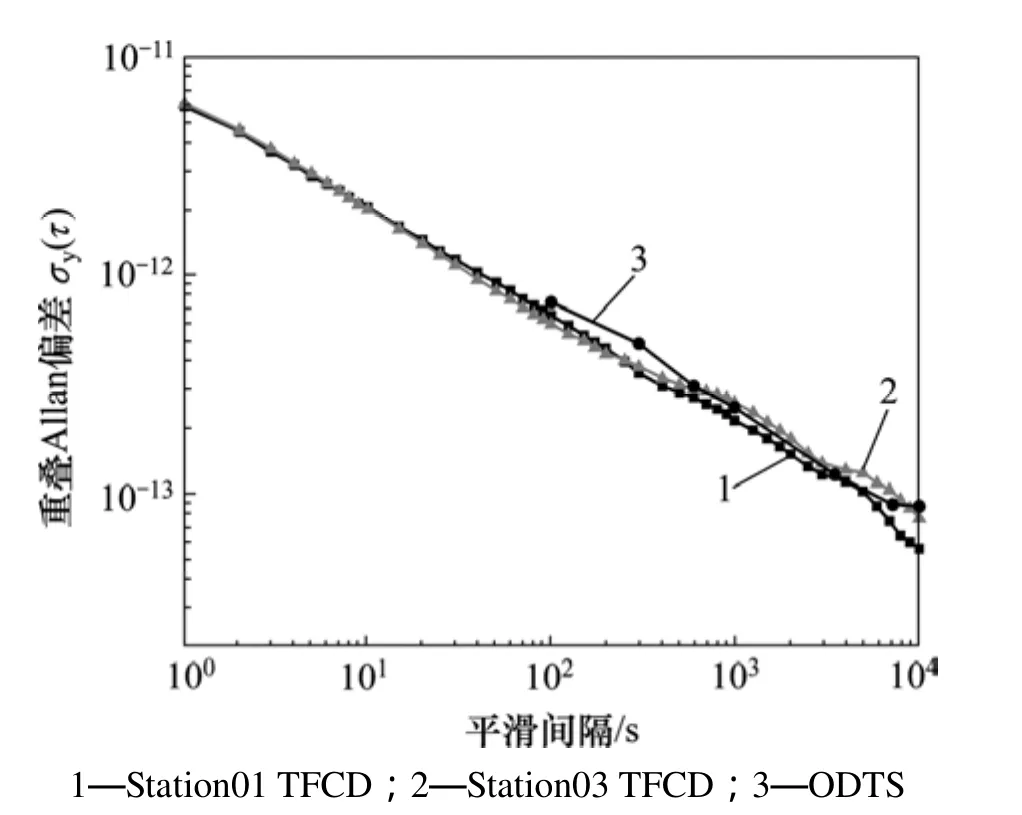
图3 TFCD法与ODTS法结果比较Fig. 3 Results comparison between TFCD and ODTS methods

图3 中Station01 TFCD为利用本文方法对监测站01观测数据的评估结果；Station03 TFCD为利用本文方法对监测站03观测数据的评估结果；ODTS为文献[16]给出的精密定轨与时间同步算法的结果；由图 3可见：利用本文方法获得的01和03站的计算结果一致，并且与文献[16]的结果基本一致，10 000 s平滑间隔内的相对误差小于10%，本文方法以较简单的方法实现与复杂算法相当的精度，说明本文方法的有效性。

4 北斗星载钟短稳评估结果

利用本文方法对2012年12月为止北斗在轨运行的所有14颗卫星星载钟(均为铷钟)的短期稳定度进行评估，基于监测站01的B1，B2和B3三频载波多普勒观测数据，观测时间段与图2相同，结果如图4所示(为反映星载铷钟的频漂特性，图中结果没有扣除频漂影响)：

由图4可见：14颗卫星的星载钟短期稳定度特性基本一致，统计平均结果如表1所示，100～1 000 s的结果与文献[16]给出的结果一致。

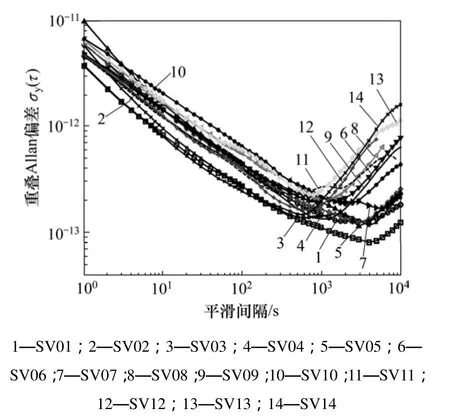
图4 14个北斗星载钟的短稳评估结果Fig. 4 Frequency stability of 14 BDS on-board clocks using TFCD method

表1 目前北斗星载钟短稳的平均特性Table 1 Average frequency stability of current BDS on-boardclocks

5 结论

(1) 提出一种适合北斗系统的利用三频载波多普勒组合的星载钟短稳单站评估方法，利用北斗观测数据对该方法进行有效性验证。结果表明：本文方法与ODTS法及SBE法计算的结果相符，对10 000 s平滑间隔内的短稳评估相对误差小于10%，以较简单的方法实现了与复杂算法相当的精度。最后利用该方法对目前北斗系统所有 14颗在轨卫星的星载钟短稳进行评估，结果基本一致：1 s稳定度约为6×10−12，1 000 s稳定度约为 2×10−13。

(2) 本文为目前处于系统建设初期的北斗系统一般用户获得星载钟短稳特性提供一种简单实现方法，同样适用于Galileo及其他GNSS系统。

[1]贾小林, 冯来平, 毛悦. GPS星载钟性能评估[J]. 时间频率学报, 2010, 33(2): 115−120.JIA Xiaolin, FENG Laiping, MAO Yue. Performance evaluation of GPS on-board clock[J]. Journal of Time and Frequency, 2010,33(2): 115−120.

[2]Dow J M, Neilan R E, Rizos C. The International GNSS Service in a changing landscape of Global Navigation Satellite Systems[J]. Journal of Geodesy, 2009, 83(7): 191−198.

[3]Oaks J, Buisson J, Largay M M. A summary of the GPS constellation clock performance[C]// Proceedings of the 39th Precise Time and Time Interval (PTTI) Applications and Planning Meeting. Long Beach, California, USA: Curran Associates, 2007: 119−130.

[4]Waller P, Gonzalez F, Hahn J, et al. In-orbit performance assessment of GIOVE clocks[C]// Proceedings of the 40th Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting. Reston, Virginia, USA: Curran Associates,2008: 69−82.

[5]Gonzalez F, Waller P. GNSS clock performance analysis using one-way carrier phase and network methods[C]// Proceedings of the 39th Precise Time and Time Interval (PTTI) Applications and Planning Meeting. Long Beach, California, USA: Curran Associates, 2007: 403−414.

[6]Delporte J, Boulanger C, Mercier F. Simple methods for the estimation of the short-term stability of GNSS on-board clocks[C]// Proceedings of the 42nd Annual Precise Time and Time Interval (PTTI) Systems and Applications Meeting. Reston,Virginia, USA: Curran Associates, 2010: 215−224.

[7]GONG Hang, YANG Wenke, WANG Yong, et al. Comparison of short-term stability estimation methods of GNSS on-board clock[C]// China Satellite Navigation Conference (CSNC) 2012 Proceedings, Lecture Notes in Electrical Engineering 160, Berlin:Springer, 2012: 503−513.

[8]ZHOU Shanshi, HU Xiaogong, WU Bin, et al. Orbit determination and time synchronization for a GEO/IGSO satellite navigation constellation with regional tracking network[J]. Science China Physics, Mechanics and Astronomy,2011, 54: 1089−1097.

[9]Dong L. IF GPS signal simulator development and verification[D]. Calgary: University of Calgary. Department of Geomatics Engineering, 2003: 30−37.

[10]Parkinson B W, James J, Spilker J. Global positioning system:Theory and applications[M]. Washington DC: American Institute of Aeronautics and Astronautics Inc., 1996: 132−134, 489−490.

[11]IEEE Standard 1139—2008, IEEE standard definitions of physical quantities for fundamental frequency and time metrology-Random instabilities[S].

[12]GONG Hang, ZHU Xiangwei, WANG Feixue, et al. Frequency stability measurement method including anomalies detection[C]// Proceedings of the 2012 International Conference on Information Technology and Software Engineering, Lecture Notes in Electrical Engineering 210, Berlin: Springer, 2013:430−440.

[13]伍岳. 第二代导航卫星系统多频数据处理理论及应用[D]. 武汉: 武汉大学测绘学院, 2005: 28−33.WU Yue. The theory and application on multi-frequency data processing of GNSS2[D]. Wuhan: Wuhan University. School of Geodesy and Geomaics, 2005: 28−33.

[14]刘文祥. 卫星导航系统高精度处理与完好性监测技术研究[D].长沙: 国防科学技术大学研究生院, 2011: 17−35.LIU Wenxiang. Study on techniques of accuracy augmenting and integrity monitoring in satellite based navigation system[D].Changsha: Graduate School of National University of Defense Technology, 2011: 17−35.

[15]王梦丽, 王飞雪. 三种电离层延迟多频修正算法的比较[J].测绘科学, 2008, 33(4): 58−60.WANG Mengli, WANG Feixue. Three multi-frequency correction methods’ comparison of ionospheric delay[J]. Science of Surveying and Mapping, 2008, 33(4): 58−60.

[16]韩春好, 刘利, 蔡志武, 等. 北斗星载原子钟时间同步与在轨性能评估[R]. 广州: 第三届中国卫星导航学术年会特邀报告,2012.HAN Chunhao, LIU Li, CAI Zhiwu, et al. Time synchronization and in-orbit performance assessment of compass on-board clocks[R]. Guangzhou: Invited Presentation of 3rd China Satellite Navigation Conference, 2012.