裂缝性地层水力裂缝非平面延伸特征分析

任岚，赵金洲，胡永全，裴钰

(1. 西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都，610500；

2. 中石油川庆钻探工程有限公司 地质勘探开发研究院，四川 成都，610500)

矿场压裂实践证实裂缝性地层水力裂缝可能会延伸为复杂的网络裂缝体系[1−2]。室内实验研究表明在低逼近角和低应力差下水力裂缝倾向沿天然裂缝转向延伸[3−9]。Blanton[10]认为当天然裂缝内流体压力超过作用在其上的正应力时天然裂缝将发生张开破裂。Renshaw等[11]基于摩擦理论建立了水力裂缝与天然裂缝正交作用准则，认为天然裂缝界面摩擦因数越小，水力裂缝越容易沿天然裂缝扩展。Potluri等[12]基于现有的相交作用准则，就天然裂缝对水力裂缝延伸路径的影响进行了系统分析。近年来，不少研究者采用数值模拟方法对裂缝性地层天然裂缝对水力裂缝延伸影响进行了研究分析[13−16]，研究结果基本证实了室内实验的可靠性，同时也证实水力裂缝延伸受到地应力非均质性、岩石强度、天然裂缝胶结状况和逼近角等多因素的影响。目前的研究集中在裂缝性地层水力裂缝扩展方向和影响因素分析上，而没有对水力裂缝非平面延伸特征进行相关研究和讨论。本文作者建立了裂缝性储层水力裂缝延伸的数学模型和相应的数值求解方法，分析裂缝性地层水力裂缝非平面延伸特征。

1 水力裂缝相交天然裂缝的延伸方向判断

采用Blanton准则[10]和Potluri[12]准则的修正方程判断水力裂缝延伸方向。当天然裂缝内的流体压力超过垂直作用在天然裂缝面上的正应力σn，天然裂缝张开破裂：

其中：

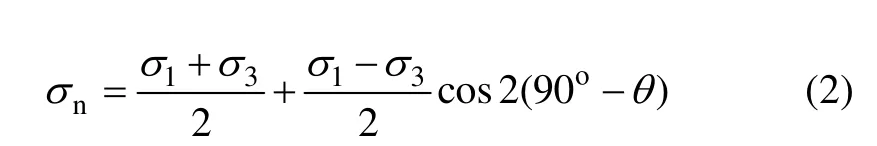
式中：σ1为水平最大地应力，MPa；σ3为水平最小地应力，MPa；θ为天然裂缝与水平最大地应力的夹角，也称逼近角，(°)。

当水力裂缝与天然裂缝交点处的流体压力大于σt+To，水力裂缝穿过天然裂缝：

式中：To为岩石的抗张强度，MPa。

其中：

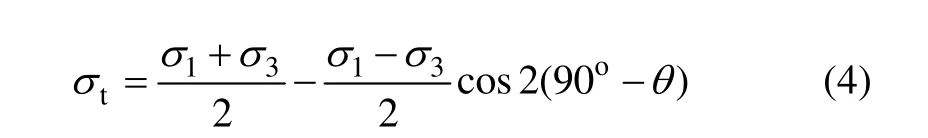
采用式(1)和式(3)可以判断水力裂缝延伸路径。

2 沿天然裂缝转向延伸的等效平面裂缝

水力裂缝相交天然裂缝后的延伸路径会出现2种情况，一是沿天然裂缝转向延伸；二是穿过天然裂缝直接延伸。图1描述了上述2种情况的延伸路径。

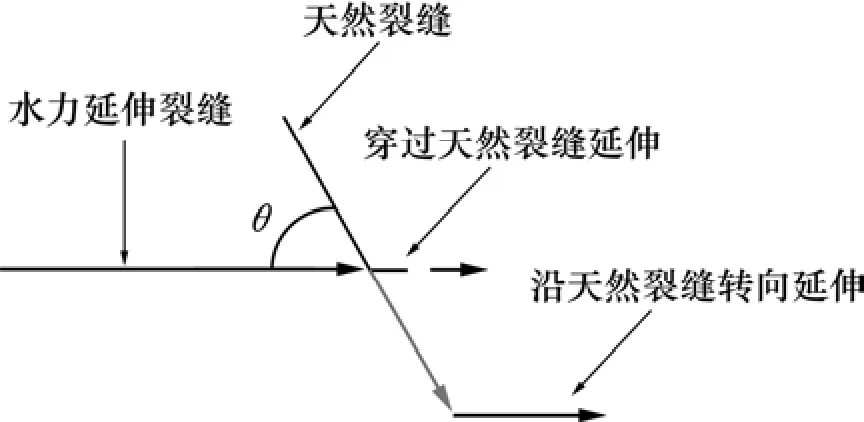
图1 水力裂缝相交天然裂缝后的不同延伸路径Fig. 1 Different propagation pathway of hydraulic fracture intersecting with natural fracture

若水力裂缝直接穿过天然裂缝，水力裂缝为平面裂缝，这时候作用在延伸裂缝上的正应力等于远场最小地应力σ3，为连续分布。若水力裂缝沿天然裂缝转向延伸，对于延伸裂缝中的天然裂缝转向段，作用在延伸裂缝上的正应力等于σn。这时候整个延伸裂缝上的正应力为非连续分布。将图1中转向延伸路径用非连续正应力分布的平面裂缝表示，可得到水力裂缝沿天然裂缝转向延伸路径的等效平面裂缝，如图2所示。

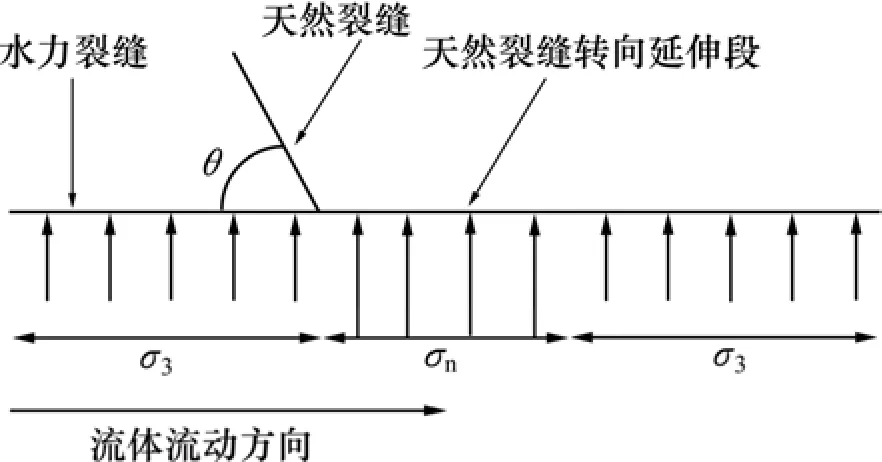
图2 水力裂缝转向延伸的等效裂缝延伸路径Fig. 2 Equivalent propagation pathway of hydraulic fracture extending along natural fracture

3 裂缝延伸的数学模型

3.1 模型假设

在模型建立时做以下假设：(1) 裂缝张开变形为线弹性行为；(2) 流体为黏性牛顿流体，不考虑缝端流体滞后现象；(3) 水力裂缝垂直剖面为椭圆；(4) 天然裂缝为垂直缝，水力裂缝和天然裂缝高度都等于油层厚度；(5) 水力裂缝前沿为自由移动边界。

3.2 裂缝缝宽方程

基于 England和 Green[17]推导的缝宽方程，考虑垂向上的平面应变假设，忽略了垂直方向上的流体压力梯度，由于裂缝延伸路径上水力裂缝受到的正应力σn(x)可能不连续，为此，在裂缝延伸路径上任何位置处裂缝剖面中心宽度为：

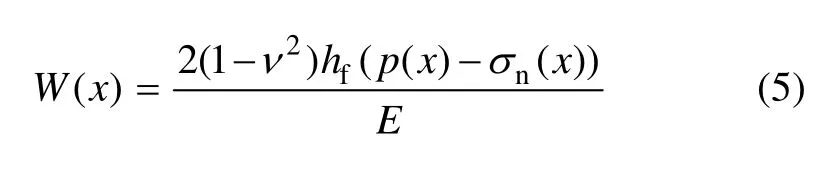
式中：W(x)为延伸路径上x处的最大缝宽，m；E为岩石弹性模量，MPa；hf为裂缝缝高，m；ν为岩石泊松比；σn(x)为延伸路径上x处裂缝面受到的正应力，MPa；p(x)为延伸路径上x处的流体压力，MPa。

3.3 缝内流体流动方程

由于压裂液的流动，裂缝内的流体压力不为常数，取决于注入排量q和流体黏度μ，在宽度为W的平行平板内的牛顿流体流动方程为：

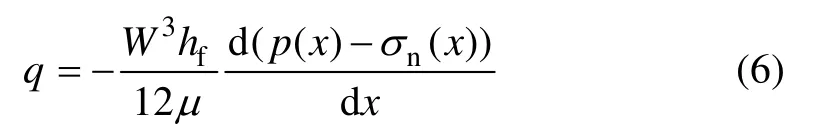
Lamb[18]认为椭圆形裂缝内的流动压降是平行板内的16/3π倍，修正的流动方程为：

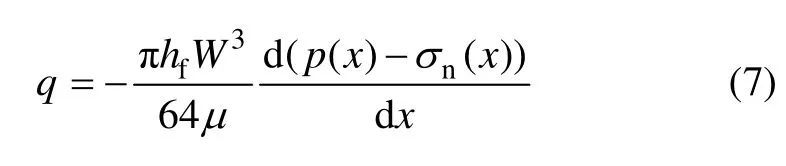
3.4 物质平衡方程

注入裂缝内的流体量等于裂缝体积变化量和滤失量之和，可得物质平衡方程为[19]：

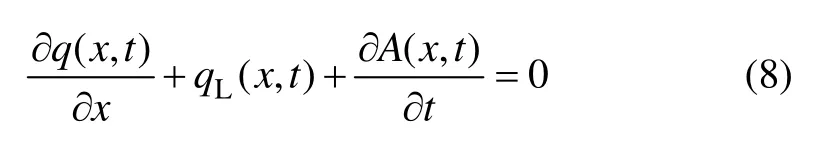
式中：q(x,t)为流过x位置点裂缝横截面的体积流量，m3/min；qL(x,t)为x位置点单位裂缝长度滤失到地层的体积流量，m2/min；A(x,t)为x位置点裂缝的横截面面积，m2；t为压裂施工时间，min。

qL(x,t)可通过Carter滤失模型计算[20]：

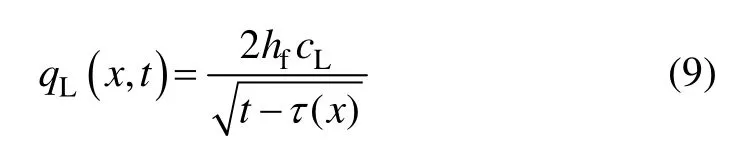
式中：τ(x)为裂缝中x点开始滤失的时间，min；cL为压裂液滤失系数，m/min1/2。

裂缝横截面面积为：

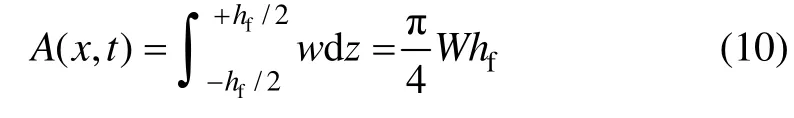
将式(7)、式(9)和式(10)代入式(8)可得：

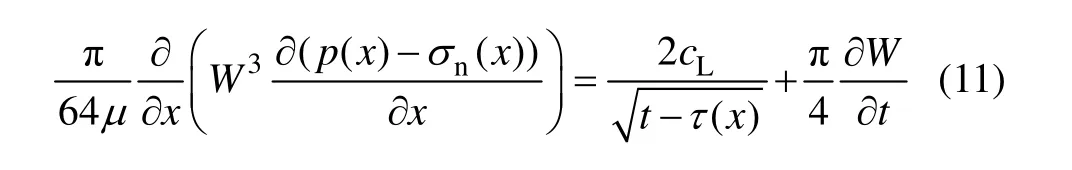
3.5 求解条件

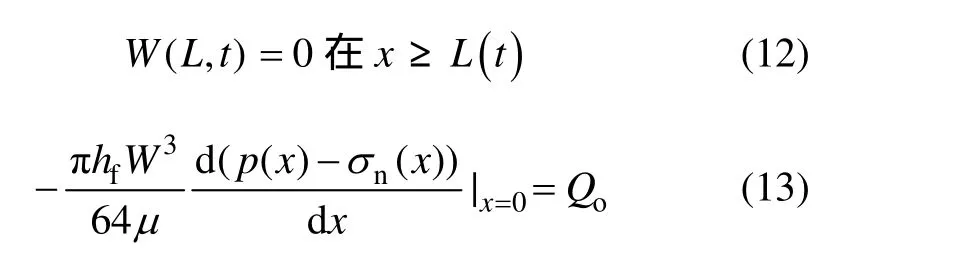
式中：L(t)为施工时间为t时刻的裂缝延伸长度，m；Qo为注入排量，m3/min。

3.6 压裂液的滤失计算

基质的滤失采用滤失模型式(9)计算。水力裂缝与天然裂缝交点处的滤失采用 Dong[21−22]推导的等效滤失系数方法计算。交点处的滤失系数为：

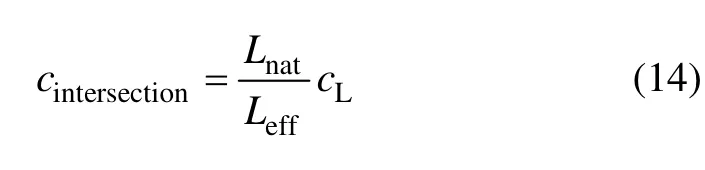
式中：Lnat为天然裂缝参与滤失的长度，m；Leff为水力裂缝垂直方向上在1 s内压力上升到水力裂缝内压力90%的最大距离。

3.7 时间步长的计算

求解模型中，水力裂缝前缘为自由边界，为了探测水力延伸裂缝是否相遇天然裂缝，因此，假设每一时间步在裂缝前缘增加相等长度的缝长增长量Δx，这样将会导致每一时间步的时间变化量Δt为求解变量。基于流量Qo满足裂缝存储和滤失两者的体积平衡，可以得到关于时间变化量Δt的求解方程为：

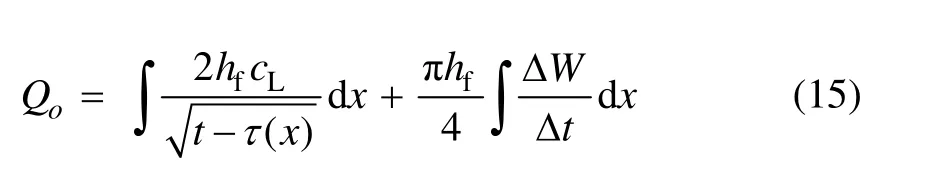
4 数学模型的求解方法

描述水力裂缝延伸的式(5)和式(11)为非线性方程组，采用隐式有限差分法进行求解。

4.1 物质平衡方程的差分格式

与经典 PKN 模型求解不同[23−24]，文中的修正模型选择缝内流体压力为求解变量，沿缝长方向进行网格剖分，采用中心差分格式，可得物质平衡方程的有限差分方程为：

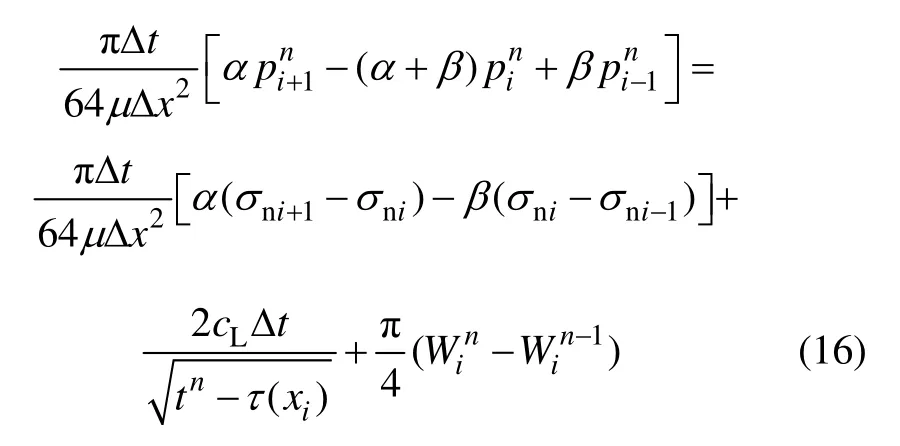
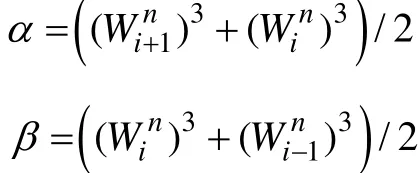
式(16)构成了压力变量pi的三对角方程组(i=1,2, …,N)。然而，Win，α和β也为未知变量，缝宽方程式(5)描述了缝宽与流体压力之间的关系为：

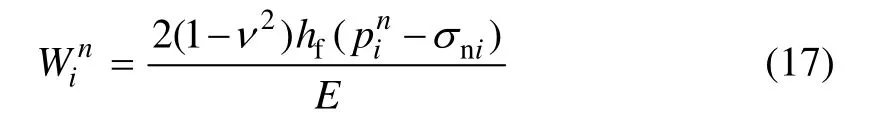
可见，式(16)和式(17)存在变量相互作用和影响，为此，每个时间步都需要采用它们一起进行耦合求解。

4.2 时间步长的离散计算

对式(15)在缝长方向上离散，可得：

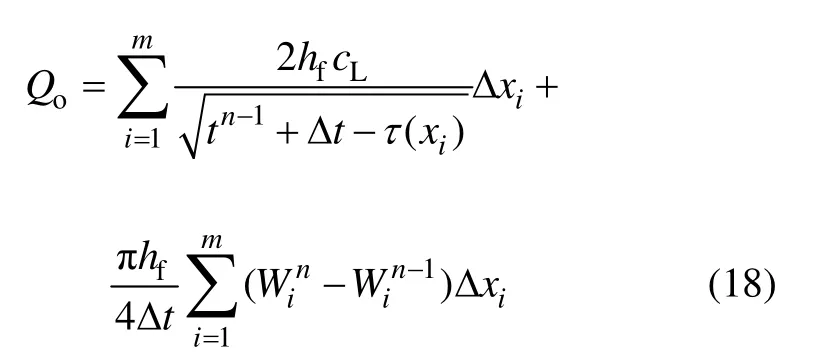
式中：m为当前时间步的裂缝网格数。

5 计算与讨论

基于本文建立的裂缝延伸模型求解方法，采用东部某油田基本参数，对水力裂缝转向延伸特征进行计算讨论。基本参数：水平最大地应力44 MPa；水平最小地应力39 MPa；岩石弹性模量2.5×104MPa；岩石抗张强度4.5 MPa；岩石泊松比0.22；压裂液黏度120 mPa·s；压裂液滤失系数 5.4×10−4m/min0.5；注入排量5 m3/min；水力裂缝高度20 m；水力裂缝延伸长度80 m；天然裂缝离井眼距离20 m；天然裂缝半长10 m。

图3给出了水力裂缝转向延伸(逼近角为30°)和直接延伸(逼近角为 80°)情况下水力裂缝延伸路径上最大缝宽变化规律。从图3可见：穿过天然裂缝直接延伸的缝宽为连续分布；而沿天然裂缝转向延伸的缝宽则为非连续分布，在转向延伸段明显减小，这是由于转向段裂缝面受到的正应力大于非转向段导致的作用结果。

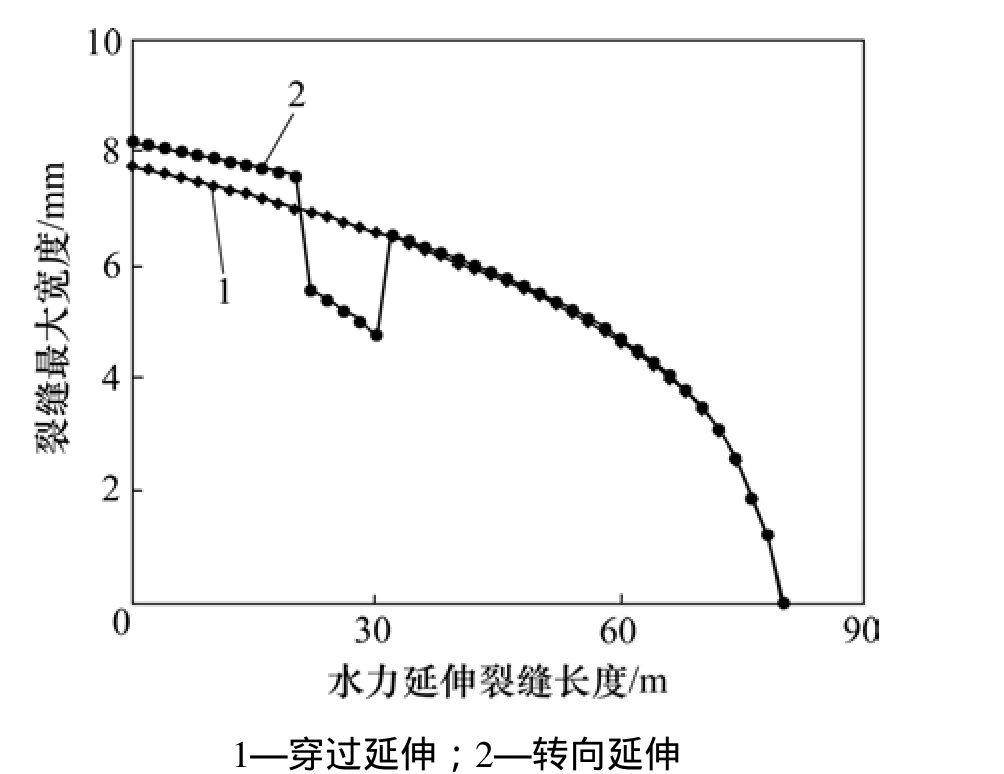
图3 不同延伸模式下裂缝缝长方向上的宽度分布Fig. 3 Maximum fracture width distribution along length direction of hydraulic fracture for different propagation modes

图4 给出了水力裂缝转向延伸(逼近角为30°)和直接延伸(逼近角为 80°)情况下水力裂缝延伸路径上的流体压力分布。相比直接延伸，转向延伸时受转向段(20～30 m)节流效应导致流体压力梯度增加的影响，使得转向段到井眼的缝内流体压力有一定程度的上升，结合图3可见，这种作用效应将导致从转向段到井眼的缝宽有一定程度的增加。

图5给出了转向延伸段分别为10 m和20 m长情况下水力裂缝延伸路径上流体压力分布。由图5可见：转向裂缝长度越长，井底压力增加越多，这是由于转向段越长导致转向裂缝段节流效应越强产生的作用结果。

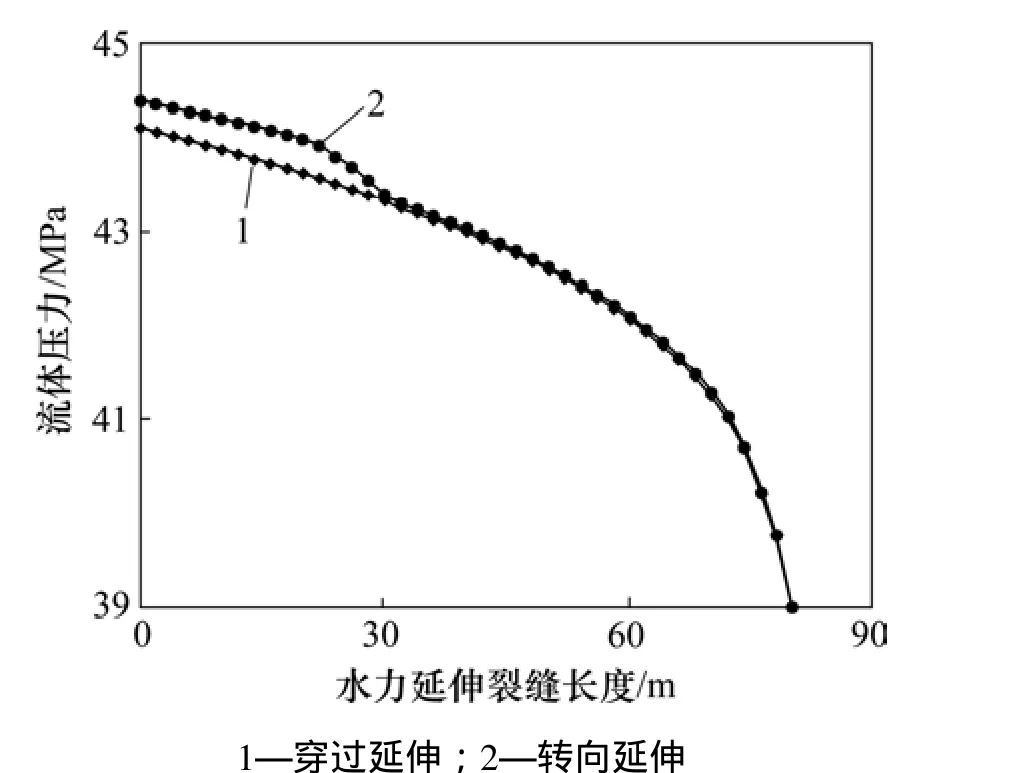
图4 不同延伸模式下裂缝缝长方向上的流体压力分布Fig. 4 Fluid pressure distribution along length direction of hydraulic fracture for different propagation modes

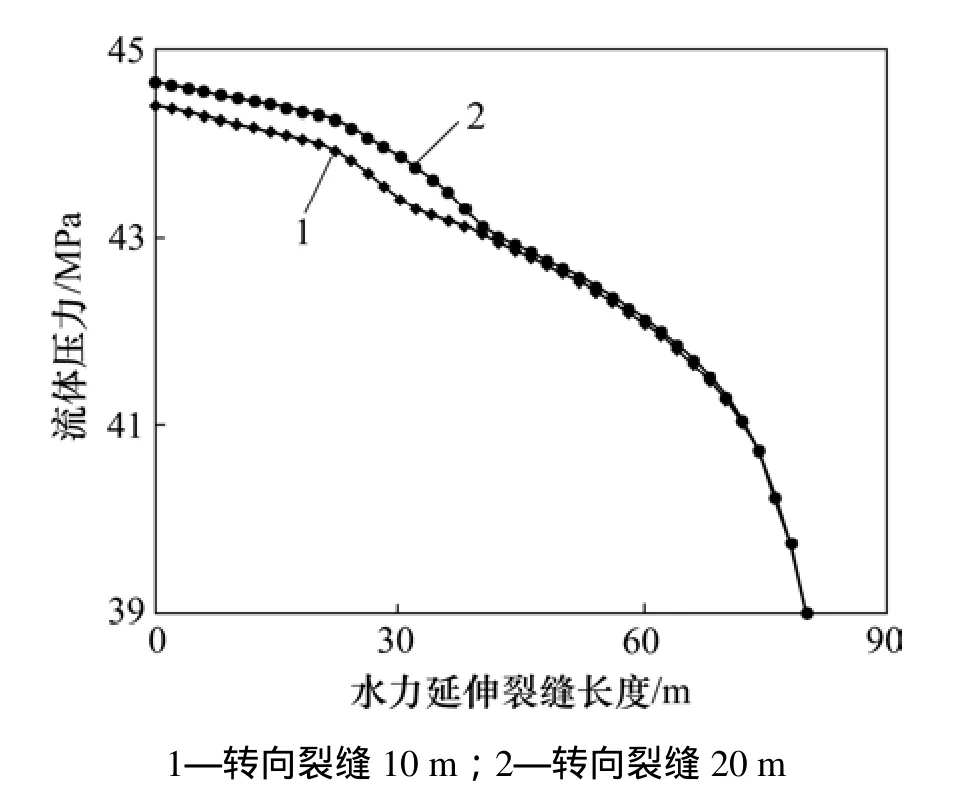
图5 不同转向长度下裂缝缝长方向上的流体压力分布Fig. 5 Fluid pressure distribution along length direction of hydraulic fracture for different reorientation length

图6 显示了不同转向段长度对水力裂缝延伸路径上缝宽分布的影响。由图6可见：转向延伸裂缝长度越长，缝宽减小的范围越大，但缝宽减小的幅度却变小。这是由于转向段越长，转向段节流效应越强导致缝内流体压力增加的越多，从而导致转向段内的缝宽又有小幅度增加。

图7显示了不同转向次数对水力裂缝延伸路径上流体压力分布的影响。由图7可见：水力裂缝转向延伸次数越多，缝内的流体压力越高，且流体压力发生影响的范围也越大。

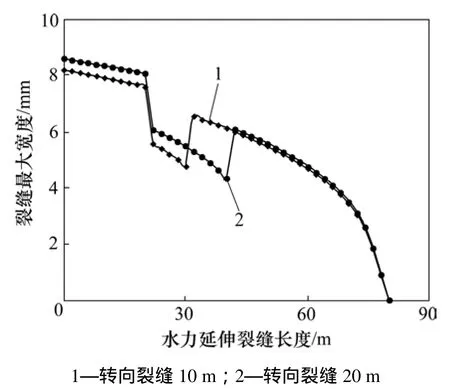
图6 不同转向长度下裂缝缝长方向上的宽度分布Fig. 6 Maximum fracture width distribution along length direction of hydraulic fracture for different reorientation length

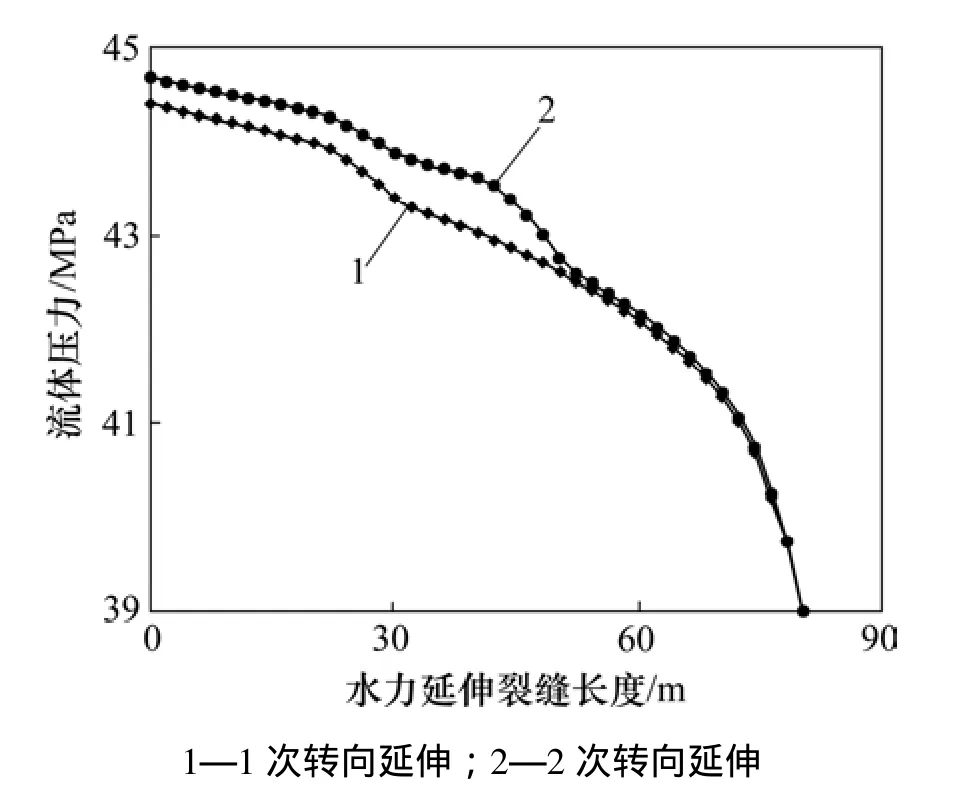
图7 不同转向次数下裂缝缝长方向上的流体压力分布Fig. 7 Fluid pressure distribution along length direction of hydraulic fracture for different reorientation number of times

图8 显示了不同转向次数对水力裂缝延伸路径上缝宽分布的影响。由图8可见：无论是1次转向还是多次转向，水力裂缝转向延伸段的缝宽都有明显的减小，受多次转向对缝内流体压力升高的影响，在相同转向段，2次转向下的缝宽较1次转向下的缝宽要宽。

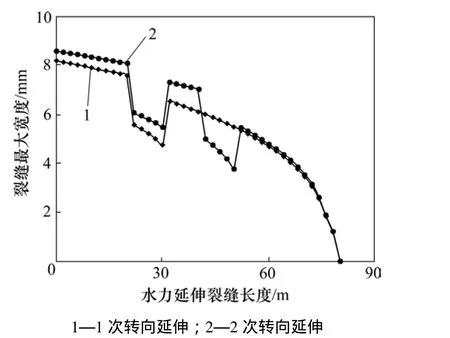
图8 不同转向次数下裂缝缝长方向上的宽度分布Fig. 8 Maximum fracture width distribution along length direction of hydraulic fracture for different reorientation number of times

6 结论

(1) 模拟计算表明，水力裂缝沿天然裂缝转向延伸时，水力裂缝在延伸路径上的缝宽为非连续分布，在转向延伸段的缝宽明显减小，转向段流体压力梯度增大，导致井底施工压力升高。

(2) 水力裂缝转向延伸次数越多或转向延伸段长度越长，水力裂缝延伸方向上缝宽减小范围越大，井底施工压力上升的越高，对压裂施工的影响则越大。

(3) 建立的裂缝性地层水力裂缝延伸数学模型可用来模拟裂缝性地层中水力裂缝非平面延伸的裂缝几何形态特征和流体压力变化规律，为裂缝性地层压裂工艺参数优化设计提供了理论依据，具有重要的理论价值和现实意义。

[1]Urbancic T I, Maxwell S C. Microseismic imaging of fracture behavior in naturally fractured reservoirs[R]. SPE 78229, 2002.

[2]Fisher M K, Wright C A, Davidson B M, et al. Integrating fracture mapping technologies to optimize stimulations in the Barnett Shale[R]. SPE 77441, 2002.

[3]Daneshy A A. Hydraulic fracture propagation in the presence of planes of weakness[R]. SPE 4852, 1974.

[4]Blanton T L. An experimental study of interaction between hydraulically induced and pre-existing fractures[R]. SPE 10847,1982.

[5]Warpinski N R. Hydraulic fracturing in tight, fissured media[J].JPT, 1991, 43(2): 146−151.

[6]陈勉, 庞飞, 金衍. 大尺寸真三轴水力压裂模拟与分析[J]. 岩石力学与工程学报, 2000, 19(增刊): 868−872.CHEN Mian, PANG Fei, JIN Yan. Experiments and analysis on hydraulic fracturing by a large-size triaxial simulator[J]. Chinese Journal of Rock Mechanics and Engineering, 2000, 19(Suppl):868−872.

[7]周健, 陈勉, 金衍, 等. 裂缝性储层水力裂缝扩展机理试验研究[J]. 石油学报, 2007, 28(5): 109−113.ZHOU Jian, CHEN Mian, JIN Yan, et al. Experimental study on propagation mechanism of hydraulic fracture in naturally fractured reservoir[J]. Acta Petrolei Sinica, 2007, 28(5):109−113.

[8]周健, 陈勉, 金衍, 等. 多裂缝储层水力裂缝扩展机理试验[J].中国石油大学学报(自然科学版), 2008，32(4): 51−54.ZHOU Jian, CHEN Mian, JIN Yan, et al. Experiment of propagation mechanism of hydraulic fracture in multi-fracture reservoir[J]. Journal of China University of Petroleum (Edition of Natural Science), 2008, 32(4): 51−54.

[9]陈勉, 周健, 金衍, 等. 随机裂缝性储层压裂特征实验研究[J].石油学报, 2008, 29(3): 431−434.CHEN Mian, ZHOU Jian, JIN Yan, et al. Experimental study on fracturing features in naturally fractured reservoir[J]. Acta Petrolei Sinica, 2008, 29(3): 431−434.

[10]Blanton T L. Propagation of hydraulically and dynamically induced fractures in naturally fractured reservoirs[R]. SPE 15261,1986.

[11]Renshaw C E, Pollard D D. An experimentally verified criterion for propagation across unbonded frictional interfaces in brittle,linear elastic materials[J]. International Journal of Rock Mechanics and Mining Science ＆ Geomechanics Abstracts,1995, 32(3): 237−249.

[12]Potluri N, Zhu D, Hill A D. Effect of natural fractures on hydraulic fracture propagation[R]. SPE 94568, 2005.

[13]Jeffrey R G, Zhang X, Thiercelin M. Hydraulic fracture offsetting in naturally fractured reservoirs: quantifying a long-recognized process[R]. SPE 119351, 2009.

[14]Akulich A V, Zvyagin A V. Interaction between hydraulic and natural fractures[J]. Fluid Dynamics, 2008, 43(3): 428−435.

[15]Rahman M M, Aghighi A, Rahman S S. Interaction between induced hydraulic fracture and pre-existing natural fracture in a poro-elastic environment: Effect of pore pressure change and the orientation of natural fracture[R]. SPE 122574, 2009.

[16]Taleghani A D, Olson J E. Numerical modeling of multi-stranded hydraulic fracture propagation: accounting for the interaction between induced and natural fractures[R]. SPE 124884, 2009.

[17]England A H, Green A E. Some two-dimensional punch and crack problems in classical elasticity[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1963, 59:489−500.

[18]Lamb H. Hydrodynamics[M]. New York: Dover Publications,1932: 581−587.

[19]Charlez P A. Rock mechanics: Petroleum applications[M]. Paris:Editions Technip, 1997: 264−266.

[20]Carter R D. Derivation of the general equation for estimating the extent of the fractured area, Appendix of optimum fluid characteristics for fracture extension[R]. New York: Drilling and Production Practice, American Petroleum Institute, 1957:261−270.

[21]Dong C. Acidizing of naturally-fractured carbonate formations[D]. Austin: University of Taxes at Austin. School of Petroleum and Geosystems Engineering, 2001: 79−84.

[22]Dong C, Zhu D, Hill A D. Acid penetration in natural fracture networks[R]. SPE 68927, 2001.

[23]Perkins T K, Kern L R. Widths of hydraulic fracture[J]. JPT,1961, 13(9): 937−949.

[24]Nordgren R P. Propagation of a vertical fracture[J]. SPEJ, 1972,12 (4): 306−314.