基于质点耦合运动学的筛分原理分析及筛分机设计

郭书立，马浏轩，孙晓冰

（1.佳木斯大学 机械工程学院，黑龙江 佳木斯 154007；2.长春理工大学 光电信息学院，长春 130012）

0 引言

颗粒物料的分级分类对其商品化具有特殊意义。美国Alle Electronics 公司研制技术装备可分选果实、蔬菜、果仁及各种小食品的“Inspecttronic”装置［1－2］；Autoline 公司的水果分级设备在世界上处于领先地位，其产品已经系列化（5 个型号），能够按照重量、颜色、形状分级；日本把成熟度、色彩传感器与自动化分级、包装线连在一起，率先实现了高度自动化的无损伤检测选果［3］；韩国SEHANTECH 株式会社是生产果蔬分选机的专业生产厂家［4］。国内目前生产的分级设备基本还限于机械分级阶段，主要进行大小、重量的分级，基于计算机视觉的水果大小分选机虽已用于实际生产，但由于价格昂贵，还未能推广使用。另外果品质量检测中使用的自动检测生产线多为进口设备，这种进口设备是针对大农场生产设计的，在我国小农户产品的检测中并不实用［5－7］。为此，分析和研究物料在筛分过程中的运动特性，寻求筛分效果最佳组合，很有必要。

1 单颗粒质点运动学分析

平面振动式筛分和滚筒式筛分是目前市场上应用广泛的两种筛分方式，而耦合筛分是在前两种方式的基础上提出的；对筛分过程中单颗粒质点的运动规律的数学模型表达有助于从理论上分析工作原理。本文主要分析各自的单颗粒质点运动规律。

1.1 平面振动筛分

物料颗粒在平面振动筛分的运动过程可描述为：振动筛面在简谐激振力F 的作用下，与物料颗粒发生碰撞，碰撞过程极短，振动筛面与颗粒分离，随之物料颗粒被抛起；在物料颗粒下落过程中与振动筛面再次发生碰撞，如此往复直至完成筛分过程［8－9］。图1 所示为振动筛与单颗粒质点间的关系模型，建立如图所示的坐标系，X 轴平行于筛面方向，Y轴与筛面垂直。其中α 为筛面倾角，β为振动筛的振动方向角。相邻2 次碰撞间振动筛的运动微分方程为：

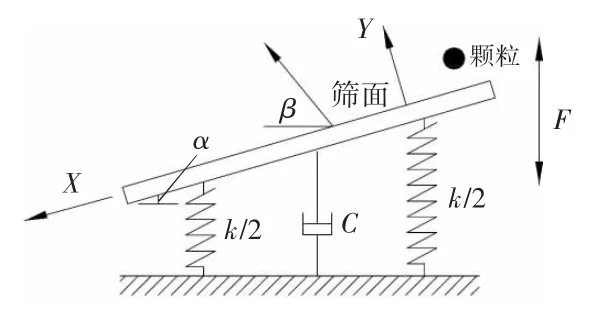
图1 物料颗粒在振动筛面上的关系模型

式中：c 为阻尼系数，k 为弹簧刚度，F 为简谐激振力，ω 为振动筛的振动频率，γ 为初相位。

由此得出，振动筛的振动由自由振动和强迫振动叠加而成，由于阻尼的影响，自由振动在振动筛工作开始后逐渐减小，因此，只考虑振动筛的强迫振动。故式（1）特解为：x（t）=Asin（ωt+τ）。其中，A 为振幅，τ 为激振力与位移的相位差，其值分别为：

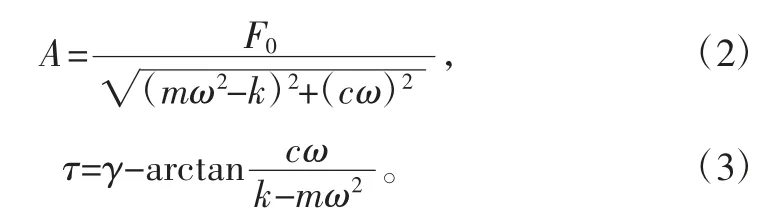
假设物料颗粒在筛面上无滑移现象，且不计物料相互间作用力。设筛面沿y 方向的位移和速度分别为x、v，则可得：

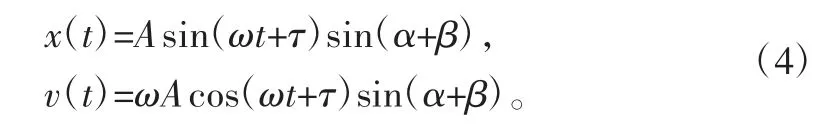
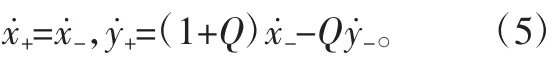
1.2 滚筒式筛分

图2 颗粒P 在滚筒筛内运动轨迹

物料颗粒在滚筒内的运动轨迹如图2 所示，其运动可分解为沿回转轴线方向的直线运动和垂直于回转轴线平面内的平面运动，其中滚筒回转轴线与水平面夹角为θ。前者是由滚筒倾斜安装而产生的，其速度即为物料通过滚筒的速度；后者与滚筒的转速密切相关。现以单颗粒质点P 为原点，建立坐标系，其运动过程为：当物料由C 进入滚筒后，随即做匀速圆周运动，并被提升至O 点，然后脱离筛面做抛物运动，当到达抛物最高点B 处后落回筛面C1处，如此循环往复，直至物料最终排出滚筒。P 在垂直于回转轴线的平面内，即XOY 平面，运动由圆周运动和抛物线运动两部分组成［10］。在研究滚筒内物料的运动规律时，假设物料颗粒随筒体的转动沿滚筒回转轴线作螺旋筛分运动；不考虑物料之间的相互作用。

下面分析单颗粒质点P 在XOY 平面内的运动。

P 尚未脱离滚筒时，其受力情况如图3 所示，在重力分力Gcosθ、滚筒筛的支撑力N、切向静摩擦力f 及离心力H 的共同作用下。随着滚筒筛的转动，在静摩擦力f 的作用下，物料随滚筒一起运动，当转到某一角度α 时，物料将下滑与滚筒筛发生相对运动。随着物料的上升，α 不断增大，重力的切向分速度Gcosθsinα 不断增大，静摩擦力f不断增大（两者保持平衡）。但其下滑力却始终小于最大静摩擦力fmax，所以颗粒P 不会下滑。当P 被带到一定高度，如图4 所示，图中为O 点，其转角为amax（最大提升角）时，摩擦力与下滑力的大小都等于最大静摩擦力，此时物料在切向方向处于滑动平衡状态。当P 转过此平衡点时，下滑力大于最大静摩擦力fmax，平衡被破坏，物料将滑动，之后发生抛落运动。在P 到达滑动平衡点之前P 的受力状态如下：

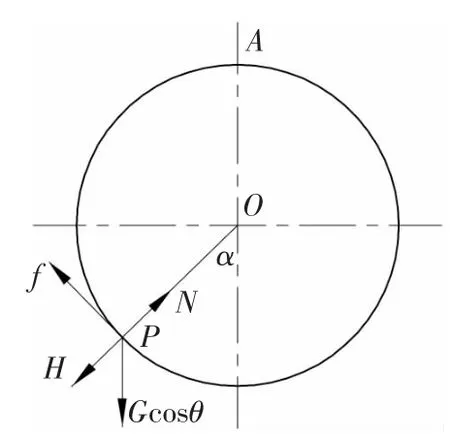
图3 颗粒P 受力图

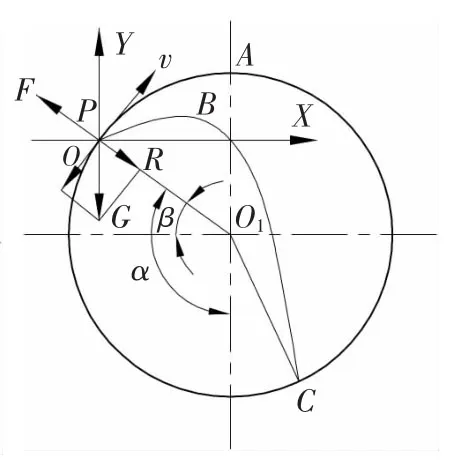
图4 颗粒P 在XOY 平面内的运动轨迹

在径向上力的平衡：

在切向上力的平衡：

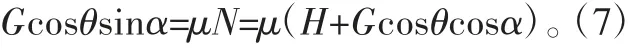
式中，θ 为滚筒筛轴线与水平面夹角，μ 为静摩擦因数，μ＝tanφ，其中φ 为静摩擦角。整理式（5）可得：

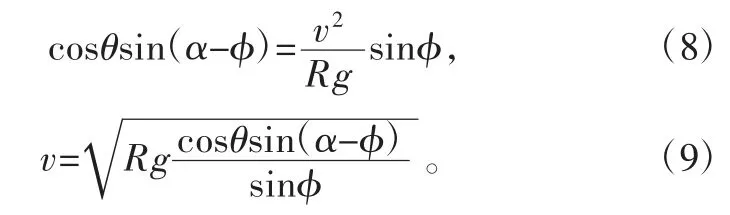
式中，v 为滚筒筛的转速。式（9）为物料提升角为α 时所需的滚筒筛转速。由此可得物料的提升角的大小与物料的静摩擦角（或静摩擦因数）、滚筒筛的转速、滚筒筛轴线与水平面夹角及滚筒筛的半径有关。

P 点的具体的运动方程如下：

圆周运动方程：

抛物线运动方程：

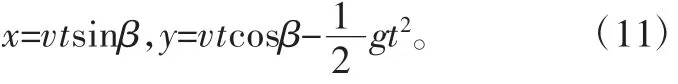
其中，R 为颗粒P 在XOY 平面内距筛体轴线的距离（即为滚筒半径）；β 为颗粒P 的脱离角；v 为在XOY 平面内颗粒P 脱离时的线速度；ω 为滚筒筛的角速度；t 为单元体P 的运动时间。由颗粒P 的运动方程可以得出其运动轨迹方程，具体如下：

圆周运动轨迹方程：

抛物线运动轨迹方程：

1.3 耦合筛分及耦合筛分质点运动学分析

耦合筛分是在滚筒式筛分的基础上，采用方法手段，使滚筒受简谐激振力作用，令物料在滚筒内既能做滚筒式筛分里的圆周运动和抛物运动，又能做平面筛分里的碰撞运动，以此实现筛分功能。

耦合筛分可视为上述两种筛分运动的叠加，在叠加过程中可能出现下述三种情况：1）当滚筒的振动周期远小于滚筒圆周运动周期时，物料只做平面振动筛分；2）物料只做滚筒式筛分。以上两种情况都达不到耦合筛分的目的。3）当滚筒的振动周期接近滚筒圆周运动周期时，物料既做平面振动筛分，又做滚筒式筛分。对第三种情况，同样取单颗粒质点P 进行运动分析。

考虑到耦合运动的先后顺序，设P 先进行圆周运动。参照滚筒筛分物料运动规律，同样可将耦合运动分解为沿回转轴线方向的直线运动和垂直于回转轴线平面内的平面运动，物料随筒体的转动沿滚筒回转轴线作螺旋筛分运动，运动轨迹与图2 大致相同。不同之处在于P 在XOY 平面上的运动轨迹。其运动过程为：P 由喂料装置进入滚筒后，进行圆周运动，当到达Oi点（不是物料最大提升高度）后，滚筒与物料发生碰撞，碰撞过程极短，当P 到达B′后，开始作抛物运动，后再次回落到滚筒C′点，重复上述过程，直至物料排出滚筒。物料P 的在XOY 平面内的运动轨迹如图5 所示。在研究物料运动过程时，假设物料颗粒在一个运动周期内，只进行一次滚筒式筛分和一次平面振动式筛分；物料颗粒间相互作用忽略不计。

单颗粒质点P 在XOY 平面内的运动分析。

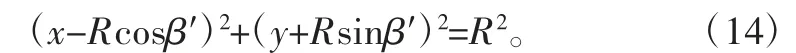
由于P 先进行圆周运动，其轨迹方程为：物料颗粒的切向速度，即线速度为：vf=ω′R。其中，R为滚筒筛半径，β′为物料P脱离角，ω′为滚筒筛角速度。当物料颗粒达到Oi点时，物料颗粒与滚筒发生碰撞，碰撞后瞬间速度矢量如图5 所示。根据对滚筒式筛分的分析，在未到达最大提升角时，物料颗粒P 在法向上的受力平衡，碰撞前、后物料颗粒P 在法向上动量守恒，从而有：

图5 碰撞后瞬间物料颗粒速度矢量图

式中，m1为滚筒筛的质量，m2为物料颗粒的质量，v10为碰撞前滚筒筛的法向速度，v1为碰撞后滚筒筛的法向速度，v2为碰撞后颗粒P 的法向速度。因为m1＞＞m2，令恢复系数Q=1，根据式（3），则有v1≈v10，v2≈2v10。在碰撞后，物料颗粒P 做抛物运动。其抛射速度v0为：

故其运动方程为：

将v0代入可得：

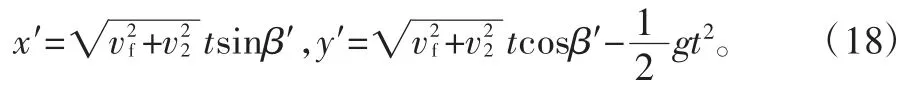
由式（16）可知，物料颗粒耦合筛分比滚筒式筛分能获得更大的抛射速度。又根据式（18）可得，XOY 平面内的运动，在X 方向上具有更大的位移；在Y 方向上能达到更高的下落点，从而（B′-C′）＞（B-C），即有更大的运动落差。从而增大了在XOY 平面内的运动周期，进而增大了物料颗粒耦合筛分运动周期，大的运动周期数有利于提高筛分效率。

2 耦合筛分机设计

整机由基座、激振装置、机架及设于机架上的复数个筛分滚筒、料斗、驱动装置、复数个输送装置、集料装置组成。采用滚筒式网筛，设计物料的筛分等级为3～4级。各筛分滚筒分别设有中心转轴，且各中心转轴分别可转动地倾斜并排固定于机架上并能分别与驱动轴传动连接。在1、2 级滚筒下方，共设有两条物料输送装置，用于把上级滚筒盛料传送至下级滚筒内。在各级滚筒的倾角处设有物料收集篓，用于收集分级目标物料。喂料装置位于1 级筛分滚筒上方，内有流量传感器及重量传感器，以便于控制喂料量及喂料速率，保证匀速喂料，从而保证最大筛分效率。在2、3 级筛分滚筒上方还设有物料引导槽，用于把筛下物料引导至下级筛分滚筒内继续筛分。筛分机机架上共设有2 个电动机，其一个带动2级滚筒的中心轴，使之成为主动轴；另一个作为物料输送装置的动力源。为使得滚筒及物料输送装置的运动同步，设计用V 带连接其余各级滚筒及另外一条物料输送装置传动。

3 耦合筛分效率影响因素分析

新型筛分机耦合了振动筛分与滚筒筛分，因此其筛分效率受这两个筛分运动方面的因素影响。除此之外，物料本身的特性也对筛分效率有较大影响。

3.1 平面振动筛分影响参数

1）振动频率。振动频率对物料在筛面上的跳动状态影响较大，它对物料在筛面上的运动周期也有很大影响。低频（5～15 Hz）时，物料几乎没有被抛起，堵筛明显，高频（40～60 Hz）时，物料跳动厉害。无论是高频筛分还是低频筛分，筛分机运行效率都偏低［11-12］。

2）振幅。其主要影响颗粒在筛面上的运动能量，大的振幅对颗粒的能量输送较大，每次可以使得颗粒弹跳更加剧烈，并且有利于物料的分层。振幅是影响筛分机结构强度的重要参数。

3）筛面倾角。筛面与水平面的夹角称为筛面倾角。倾角的大小与筛分设备的处理量和筛分效率有密切关系。当倾角增大时，将增加筛上物料的抛掷强度，从而物料在筛面上向前的运动速度加快，使筛子处理量提高，但物料在筛面停留时间缩短，减少颗粒透筛机会，使筛分效率降低。反之就会使处理量降低，从而提高筛分效率。

上述3 个参数的共同影响可归纳为一个参数——抛掷强度KV。

式中：A 为振幅；ζ 为激振频率；υ 为振动方向角；θ 为筛面倾角。

K 为振动强度。研究表明：KV=3～3.3 时，物料最易透筛；KV＜3 时，物料难透筛；KV＞3.3 时，物料过度被抛起，物料更难透筛。

3.2 滚筒式筛分影响参数

滚筒筛分主要参数包括：滚筒中心轴转速、筛面倾角、筛面开孔率等。

滚筒中心轴转速：当中心轴转动过慢，物料在筛网上的周期数减少，周期时间增加，将不利于效率的提高；而当中心转轴过快，物料在离心力的作用下会随着筛网一起转动，透筛率将大大减小。

筛面倾角：它是中心转轴与水平方向的夹角，它影响到筛孔的水平投影尺寸，同时对物料在筛面上的滑行速度也有很大影响。当倾角变大，筛孔水平投影尺寸变小，物料在垂直方向上的透筛概率降低，物料沿筛面方向的速度分量变大，生产效率提高。当倾角变小，筛孔水平投影尺寸变大，物料沿筛长方向运行速度变慢，停留时间长，垂直方向上的透筛概率增加，但处理量减小。筛面倾角可在15°～30°间选取，以保证物料在筛面上有足够的运动速度和合适的料层厚度。

筛面开孔率：开孔率为筛粒尺寸与筛粒尺寸、筛孔尺寸和之比，当开孔率大时，增大了物料的透筛概率，提高了筛分机的筛分效率。

3.3 物料相对几何特征

物料相对几何特征是指物料与筛孔的相对尺寸及物料外观形态。

物料与筛孔的相对尺寸：只有物料粒径小于筛孔尺寸，经过多次反复与筛孔接触，才有透筛的概率。颗粒透筛的概率主要取决于颗粒横截面在筛板平面上的投影与筛孔面积之比。

物料的外观形态：物料的外观形状影响物料的透筛概率，物料的平行截面越是与筛网开孔相似的，越容易透筛，条状或不规则形状易卡在筛孔中影响效率。

4 结论

基于平面振动筛分和滚筒式筛分单颗粒质点运动规律的分析，提出了耦合筛分概念。

运用运动叠加原理，构建了单颗粒质点耦合筛分运动数学模型。

理论分析表明，物料颗粒耦合筛分比滚筒式筛分能获得更大的抛射速度。物料在XOY 平面内的运动，在X 方向上具有更大的位移；在Y 方向上能达到更高的下落点，从而使物料获得更大的运动落差。这增大了在XOY 平面内的运动周期，进而增大了物料颗粒耦合筛分运动周期，而大的运动周期数有利于提高筛分效率。

根据耦合筛分运动特点，对筛分机结构进行了整体设计。分析了振动频率，振幅，筛面倾角，滚筒中心轴转速、筛面倾角、筛面开孔率及物料相对几何特征等因素对耦合筛分效果的影响，采用抛掷强度KV综合各因素的影响：KV=3～3.3 时，物料最易透筛；KV＜3 时，物料难透筛；KV＞3.3 时，物料过度被抛起，物料更难透筛。

［1］Gezer I，Haciseferogullari H，Demir F.Some physical properties of Hacihalilonglu apricot pit and its kernel［J］.Journal of Food Engineering，2002（1）：49-57.

［2］王红兵，张路霞.探析影响直线振动筛筛分效果的若干因素［J］.现代制造技术与装备，2008（4）：29-30.

［4］任斌.影响筛分过程的因素分析［J］.内蒙古科技与经济，2006（4）：103-104.

［5］Cleary P W，SAWLEY M L.DEM modeling of industrial granular flows:3D case studies and the effect of particle shape on hopper discharge［J］.Applied Mathematical Modeling，2002（26）：89-111.

［6］Standish N，Meta I A.Some kinetic aspects of continuous screening［J］.Powder Technology，1985（41）：165-171.

［7］焦红光，李靖如，赵跃民.筛孔孔径和筛面倾角优化配置的试验研究［J］.选煤技术，2007（2）：1-4.

［8］李玉凤.直线振动筛运动学参数的确定［J］.煤矿机械，2008（29）：33-34.

［9］郑炫，马铖，张景.滚杠式红枣分级机的实验方法［J］.现代农业科技，2012（19）：107-110.

［10］唐红侠，赵由才.滚筒筛筛分生活垃圾的理论研究［J］.环境工程学报，2007（12）：126-129.

［11］王桂锋，童昕，陈艳华.基于DEM 的振动筛筛分参数对筛分效率影响的研究［J］.矿山机械，2010，38（15）：102-106.

［12］蔡玉良，杨学权，丁晓龙.滚筒筛内物料运动过程的分析［J］.水泥工程，2010（2）：10-13.