钢纤维混凝土弯曲韧性及其评价方法

高丹盈，赵亮平，冯 虎，赵顺波

（1.郑州大学 土木工程学院，河南 郑州 450002；2.华北水利水电大学 土木与交通学院，河南 郑州 450008）

在荷载作用下，普通混凝土通常发生脆性破坏.随着混凝土强度的提高，其脆性显著增大.加入混凝土中的纤维能够阻止混凝土内部裂纹的产生和发展，提高混凝土的韧性，改善混凝土结构的变形和抗震性能.目前，纤维混凝土（fiber reinforced concrete，简称FRC）已广泛应用于工程建设的有关领域.

韧性指标通常用于定量描述材料、构件或结构开裂后的带裂缝工作能力、吸收能量能力以及整体生存能力（即发生大变形时所残余的强度）.目前，确定FRC韧性的试验方法有压缩、拉伸、剪切和弯曲韧性试验方法等.其中，弯曲韧性试验方法能够较好地模拟大多数工程构件的实际受力情况，且操作方法简单易行，是测定FRC耗能能力最流行的试验方法［1］，相应的弯曲韧性指标也成为衡量FRC韧性的最常 用指标［2－7］.本文结合钢纤维混凝土（steel fiber reinforced concrete，简称SFRC）试件的弯曲韧性试验结果，分析总结国内外常用弯曲韧性测试和评价方法的优点和不足，提出了一种适合钢纤维混凝土特点的弯曲韧性评价方法，并基于该方法探讨了钢纤维体积率（ρf）对普通混凝土（C30）和高强混凝土（C50）弯曲韧性的影响.

1 试验概况

试验采用的水泥为42.5普通硅酸盐水泥；碎石为粒径5～20mm、连续级配的碎石；砂为级配良好的中砂，细度模数2.64；钢纤维为切断弓形钢纤维，长径比55，抗拉强度1 250 MPa；外加剂为JKH－1型粉状高效减水剂，减水率为18%～25%（质量分数）；拌和水为饮用自来水.

按照C30 和C50 强度等级进行混凝土配合比设计，基准混凝土水灰比（质量比）分别为0.60 和0.38.为研究钢纤维体积率对混凝土弯曲韧性的影响，在C30和C50 混凝土中均掺入体积率分别为0.2%，0.4%，0.5%，0.7%，1.0%，1.5%和2.0%的钢纤维.另外，在C30 混凝土中还分别掺入体积率为2.5%和3.0%的钢纤维.

弯曲韧性试验采用尺寸为100mm×100mm×400mm 的试件，试验方法和加载制度按CECS 13：2009标准［6］进行.同时，制作了钢纤维混凝土立方体试块，标准养护28d后测试其抗压强度，试验结果见表1.

表1 钢纤维混凝土28d抗压强度Table 1 28dcompressive strength of steel fiber reinforced concrete MPa

2 试验结果及分析

不同钢纤维体积率下SFRC弯曲试件的荷载－挠度曲线见图1.由图1可以看出：普通混凝土（ρf＝0）弯曲试件荷载－挠度曲线没有下降段，其在超过峰值点后突然破坏.掺入钢纤维后，混凝土表现出明显的韧性，随钢纤维体积率增大，荷载峰值不断提高，SFRC弯曲试件的荷载－挠度曲线愈加饱满.在ρf＜1.0%时，SFRC弯曲试件的荷载－挠度曲线存在明显的软化段，随钢纤维体积率增大，软化段越来越不明显；在ρf≥1.0%时，SFRC弯曲试件的荷载－挠度曲线在一定挠度内没有明显的下降段，甚至出现二次峰值，表现出较好的持荷能力.此外，ρf＜1.0%时，SFRC弯曲试件荷载－挠度曲线峰值点的变形很小，均小于0.05mm，且随钢纤维体积率的变化规律不明显；ρf≥1.0%时，SFRC弯曲试件荷载－挠度曲线峰值点的变形明显增大，C30和C50强度等级的SFRC峰值点最大变形分别达到0.38mm 和0.51mm.

图1 不同钢纤维体积率下SFRC弯曲试件的荷载－挠度曲线Fig.1 Load－deformation curves of SFRC specimens with different steel fiber volume fractions

SFRC试件弯曲韧性试验表明，当荷载较小时，钢纤维与混凝土基体黏结较好，二者作为整体共同承担荷载，弯曲试件的荷载－挠度曲线基本呈直线.随着荷载的增大，SFRC 内部微裂缝稳定扩展成为宏观裂缝，荷载－挠度曲线逐渐非线性化.由于跨越裂缝的钢纤维通过黏结横贯裂缝传递应力，SFRC表现出较好的韧性，钢纤维体积率越大，这一特征越明显（见图1）.峰值荷载后，钢纤维与基体间界面黏结应力逐步达到极限，越来越多的钢纤维被拔出或拉断.随钢纤维体积率增大，荷载－挠度曲线软化段越来越不明显，甚至没有软化段，SFRC 呈现出裂而不断的特征［8－9］.

3 钢纤维混凝土弯曲韧性测试与评价方法

弯曲韧性评价指标是目前衡量SFRC韧性最常用的指标，许多国家都制定了钢纤维混凝土弯曲韧性试验方法标准，如美国的ASTM C 1018标准［2］、日本的JSCE－SF4标准［3］、欧洲的RILEM TC 162－TDF标准［5］和中国的CECS 13：2009标准［6］等.这些标准从不同角度定义了SFRC 弯曲韧性评价指标，包括绝对的能量吸收能力、与能量吸收能力有关的量纲为1 的韧性指数、等效弯曲强度等［1］.由于RILEM TC 162－TDF 标准［5］采用的试验方法和加载制度与本文试验差别较大，不过多介绍，下面重点讨论其他几种方法的适用性和不足之处.

3.1 ASTM C 1018标准［2］为基础的评价方法

ASTM C 1018标准［2］评价方法采用弯曲韧性指数I5，I10和I20表征SFRC的弯曲韧性.中国CECS 13：2009标准［6］评价方法就是在此基础上改进而成的.I5，I10和I20的计算公式为：

式中：δ 为初裂点对应的跨中挠度（mm）；Ωδ，Ω3.0δ，Ω5.5δ和Ω10.5δ分别为跨中挠度δ，3.0δ，5.5δ和10.5δ时荷载－挠度曲线下的面积（N·mm），即图2 中OAB，OACD，OAEF 和OAGH 所包围的面积.

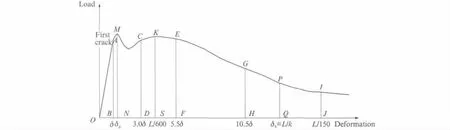
图2 弯曲韧性指数定义Fig.2 Definitions of flexural toughness indexes

该评价方法因物理意义明确，并因采用量纲为1的不受试件形状和尺寸影响的弯曲韧性指数而得到了广泛应用.但是，该方法也有不足之处：

（1）初裂点位置难以准确确定

ASTM C 1018标准评价方法的第一大缺陷是初裂点确定具有较大的人为随意性，且初裂变形的微小差异对弯曲韧性指数计算结果有很大影响.例如，对钢纤维体积率分别为1.5%和2.0%的C30混凝土，依据该方法的规定，ρf＝1.5%时混凝土的初裂点可取图3中的A″，B″，C″点，ρf＝2.0%时混凝土的初裂点可取图3中的A′，B′，C′点.按式（1）计算出各初裂点对应的混凝土弯曲韧性指标见表2.由表2可知，尽管A″，C″两点和A′，C′两点的挠度差均只有0.06mm，但按式（1）计算所得的混凝土弯曲韧性指标I20却分别相差了114%和56%之多.文献［10］也得到了相似的结论.

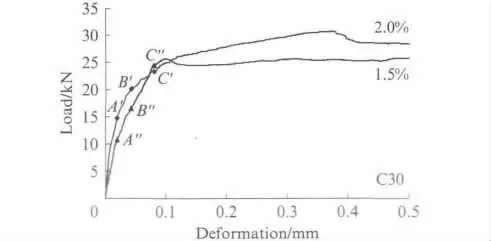
图3 依据ASTM C 1018标准评价方法确定的初裂点Fig.3 Definition of first crack according to the evaluation method in ASTM C 1018standard

为了避免确定初裂变形时的人为随意性和量测误差对弯曲韧性指标的影响，国内外研究者做出了不懈的努力.一是试图通过改进测量手段和计算方法［11－12］，以便更准确地确定初裂点，如采用声发射法，由声发射的能量突发点准确地找出初裂点［11］.二是采用与峰值荷载所对应的变形代替初裂变形作为计算弯曲韧性的初始变形，其依据是，从混凝土初裂到峰值荷载这一区段内，钢纤维对混凝土弯曲韧性的贡献很小［1，13－14］；然而，也有研究发现，对某些种类的纤维，纤维体积率较高时，纤维对这一区段内混凝土的弯曲韧性有明显提高作用［9，15］，例如，图1中钢纤维体积率超过1.0%后，混凝土荷载－挠度曲线有明显的强化段，这一阶段的能量吸收值占据相当大的比重.因此，以峰值荷载对应变形为初始变形计算得到的弯曲韧性指标的适用性值得商榷.

表2 不同初裂点对应的钢纤维混凝土弯曲韧性指数Table 2 Flexural toughness indexes of SFRC corresponding to different first crack points

（2）初裂前曲线斜率对弯曲韧性指数影响较大

ASTM C 1018标准评价方法的第二大缺陷是初裂前荷载－挠度曲线斜率对弯曲韧性指数计算结果的影响较大.以C30 强度等级的SFRC 为例，见图3，ρf＝2.0%时SFRC的韧性明显高于ρf＝1.5%时SFRC 的韧性，但弯曲韧性指数的计算结果恰恰相反（见表2）.产生这一现象的原因是：式（1）分母项Ωδ的值很小，初裂点之前荷载－挠度曲线斜率的微小差别就会使Ωδ值有很大的不同.同时，式（1）分子项Ω3.0δ，Ω5.5δ和Ω10.5δ的值相对较大，荷载－挠度曲线斜率的微小差别对其影响相对较小.由于ρf＝2.0%时SFRC 荷载－挠度曲线斜率稍大于ρf ＝1.5%时的曲线斜率，尽管差异非常小，但A′，B′，C′点相应的Ωδ值却比A″，B″，C″点相应的Ωδ值分别增大56%，37%和19%，而Ω3.0δ，Ω5.5δ和Ω10.5δ的增大幅度却相对较小，Ω10.5δ的最大增幅才达到15%，因此导致ρf＝2.0%时SFRC 的弯曲韧性指数计算结果反而有所降低.

（3）弯曲韧性指数计算结果过大

对于理想弹塑性材料，I5，I10和I20值分别等于5，10和20.理论上讲，SFRC 的弯曲韧性指数应小于理想弹塑性材料，但从表2可看出，当ρf 为1.5%和2.0%时，C30强度等级SFRC的I5，I10和I20值出现大于5，10和20的现象，文献［9］也对此提出了疑问.造成这一现象的原因是：对于理想弹塑性材料而言，其荷载－挠度曲线超过初裂点后立即变成水平段，荷载不再增长.但对于SFRC，当ρf≥1.5%时，其荷载－挠度曲线超过初裂点之后还有稳定的强化段，且在规定的计算挠度（Ω10.5δ）以内，SFRC的残余弯曲强度仍然保持较高的水平，普遍大于初裂荷载（见图1）.

（4）不适合钢纤维体积率较低的混凝土

由图1可见，ρf≤0.5%时，SFRC弯曲试件的荷载－挠度曲线存在不稳定段，即荷载突降、挠度瞬间大幅增长的斜直线段，而试验仅能测出斜直线段两端点的荷载和挠度值，无法真实反映挠度区间内的荷载变化情况.对于C30和C50强度等级的SFRC，当ρf≤0.5%时，3.0δ，5.5δ均位于荷载－挠度曲线的不稳定区域，难以对这些试件的I5和I10进行准确评价.对于C50强度等级的SFRC，当ρf 为0.2%和0.4%时，10.5δ 仍位于荷载－挠度曲线的不稳定区域，试件的I20也无法准确评价.文献［10］的研究也证明了这一点.

3.2 JSCE－SF4标准［3］为基础的评价方法

JSCE－SF4标准评价方法采用等效弯曲强度fe（MPa）评价SFRC的弯曲韧性.中国CECS 13：2009标准［6］和CECS 38：2004 标 准［7］均 借 鉴 了JSCESF4标准评价方法.等效弯曲强度fe的计算公式为：

式中：Ωk为跨中计算挠度为L／k 时弯曲试件荷载－挠度曲线下的面积（N·mm），JSCE－SF4 标准取k为150，Ωk即为图2中OMIJ 包围的面积；δk为跨中计算挠度为L／k时的挠度值（mm），取k为150；L为支座间跨度（mm）；b，h 分别为试件截面宽度（mm）和高度（mm）.

该标准评价方法具有概念明确、计算简单、不受初裂点位置影响的优点，且不稳定曲线段的面积相对于跨中计算挠度为L／150时的曲线面积也较小，荷载－挠度曲线不稳定段对等效弯曲强度影响不大.但是，该方法也有不足之处：

（1）跨中计算挠度取L／150没有充分理论依据

在大多数工程应用中，正常使用状态的容许挠度均小于L／150，将跨中计算挠度单一限定为L／150无法满足实际工程需要.鉴于此，ASTM C 1609标 准［4］在JSCE－SF4标准的基础上补充计算了跨中计算挠度为L／600时荷载－挠度曲线下的面积（图2中OMKS 包围的面积）及等效弯曲强度.与JSCE－SF4标准评价方法相比，ASTM C 1609标准评价方法有一定程度的改进，但所取特征点仍然偏少，不能全面反映出实际工程应用中SFRC的弯曲韧性水平.

（2）不同尺寸的试件无法对比分析

等效弯曲强度fe是一个有量纲的值，对于不同尺寸试件的分析比较很困难［12］.因此，CECS 13：2009标准［6］对其进行了改进，提出了弯曲韧度比（Re）指标，其计算公式为：

式中：fcr为SFRC的弯曲初裂强度（MPa）.

Re是一个量纲为1的值，其解决了不同尺寸试件的对比分析问题.但如前文所述，SFRC 的初裂点难以准确确定，故以SFRC 弯曲初裂强度为基准进行计算仍有不妥之处.

（3）等效弯曲强度与真实弯曲韧性水平有偏差

等效弯曲强度fe实质上是利用整个荷载－挠度曲线求得的一个应力平均值.但由于SFRC 弯曲试件荷载－挠度曲线在不同加载阶段起伏较大（见图1），因此fe不能真实反映特定挠度下的SFRC弯曲韧性水平.为此，有研究者提出用峰值荷载后的等效抗弯强度PCSm（MPa）来衡量SFRC的韧性［13］：

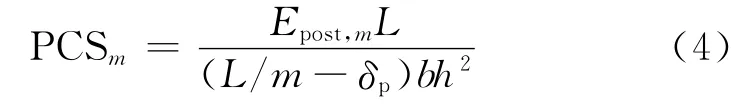
式中：Epost，m为峰值荷载后荷载－挠度曲线的面积（N·mm），即图2中NMPQ 包围的面积；δp为峰值荷载对应的跨中挠度（mm）；m 为设定值（mm），是一个变量，推荐范围为150～3 000.上述方法虽然能够更真实反映SFRC 的弯曲韧性水平，但完全不利用峰值荷载前荷载－挠度曲线的有关数据有些欠妥.

4 钢纤维混凝土弯曲韧性评价方法

钢纤维对混凝土性能的改善与混凝土所处的受力阶段有一定关系.钢纤维对混凝土峰值荷载前的改善主要表现在提高混凝土的峰值弯曲强度、峰值位移和韧性；对峰值荷载后的改善主要表现在提高峰值荷载后混凝土的残余弯曲强度和持荷能力.在现有弯曲韧性评价方法的基础上，结合本文试验结果，建议采用以下方法评价SFRC的弯曲韧性：

（1）以初始弯曲韧度比Re，p表征SFRC 达到峰值挠度前的弯曲韧性.Re，p的计算公式为：

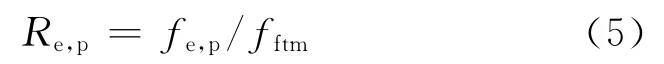
式中：fftm为钢纤维混凝土弯曲强度（MPa）；fe，p为钢纤维混凝土等效初始弯曲强度（MPa），计算公式为：

式中：Ωp为峰值挠度δp前荷载－挠度曲线下的面积（N·mm），即图2中OMN 包围的面积.

（2）以残余弯曲韧度比Re，k表征SFRC 达到峰值挠度后的残余弯曲韧性.Re，k的计算公式为：

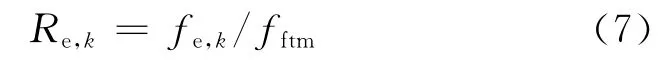
式中：fe，k为等效残余弯曲强度（MPa），计算公式为：

式中：ΩR，k为δp至δk段对应的荷载－挠度曲线下的面积（N·mm），即图2中NMPQ 包围的面积；δR，k为δp至δk段的跨中计算挠度值（mm），即：

式中：δk为给定的跨中计算挠度L／k，分别取k＝500，300，250，200，150.

与前述几种方法相比，该方法不仅避开了确定初裂点的困难，避免了荷载－挠度曲线初始上升段斜率的影响，而且便于不同尺寸试件的比较，并能适用于钢纤维体积率较低的情形.同时，Re，k可以取不同跨中计算挠度进行计算，其结果更真实地反映了SFRC的弯曲韧性水平，满足了实际工程结构计算的需要.从物理意义上来讲，Re，p反映了SFRC 达到峰值荷载前的弯曲韧性，其值越大，表示在峰值荷载前钢纤维对混凝土增强效果越好；Re，k反映了SFRC的残余弯曲韧性，其值越大，表示钢纤维对混凝土残余弯曲强度和后续持荷能力的贡献越大.

根据本文的试验结果，利用式（5）～（8）计算出各组SFRC 弯曲试件的等效初始弯曲强度、初始弯曲韧度比、等效残余弯曲强度和残余弯曲韧度比，结果见表3.

由表3 可以看出，随钢纤维体积率的增加，SFRC等效初始弯曲强度和等效残余弯曲强度总体均有显著提高。

由表3还可见，随钢纤维体积率的增加，SFRC等效初始弯曲强度总体显著增大，初始弯曲韧度比Re，p在ρf＜1.0%时有所波动，在ρf≥1.0%后的变化规律趋于稳定，总体呈现出明显的上升趋势.这是由于，一方面，钢纤维体积率较低时，其对峰值前弯曲韧性的改善主要体现在提高强度上，对变形贡献不大，因此，随钢纤维体积率的增加，fe，p显著提高，而Re，p却无明显改善.另一方面，由于此时SFRC 的峰值挠度较低，随挠度的微小波动，Re，p的变化非常敏感，受试验误差等客观因素的影响较大，呈现出一定幅度的波动.当ρf≥1.0%后，钢纤维对混凝土峰值前的强度和变形均有明显改善，SFRC 峰值挠度较大，受客观因素影响较小，因而fe，p和Re，p均呈现出总体稳定上升的特点.

从表3还可以看出，总体而言，残余弯曲韧度比随钢纤维体积率增大不断提高.对C30 混凝土，ρf从0.2%增至2.5%，Re，500和Re，150分别提高了62%和118%；对C50 混凝土，ρf 从0.2%增 至2.0%，Re，500和Re，150增幅分别达到了75%和223%.需要指出的是，随跨中计算挠度增大，各组SFRC的残余弯曲韧度比呈现出不同的变化规律.钢纤维体积率较低时，随跨中计算挠度增大，残余弯曲韧度比从Re，500到Re，150不断降低，说明此时SFRC的持荷能力较弱，残余弯曲强度随变形增大不断降低.钢纤维体积率较大时，残余弯曲韧度比随跨中计算挠度增大降幅较小，基本呈水平状，有的甚至有所提高，说明此时SFRC的持荷能力较强，残余弯曲强度较高，甚至会出现二次峰值.这些特征在C50 强度等级SFRC的表现均比C30强度等级SFRC 明显，表明在钢纤维体积率较低时，高强混凝土的脆性更大，随钢纤维体积率增大，其弯曲韧性的改善更为明显.这主要是由于高强混凝土本身脆性大，钢纤维体积率较低时，钢纤维不足以弥补这一缺陷；而钢纤维体积率较高时，由于高强混凝土密实度更大，钢纤维与基体的黏结性更好，改善作用也更为明显.

表3 等效初始弯曲强度、初始弯曲韧度比、等效残余弯曲强度和残余弯曲韧度比计算结果Table 3 Calculation results of fe，p，Re，p，fe，k and Re，k

5 结论

（1）ASTM C 1018标准评价方法用于评价SFRC弯曲韧性有明显的不足之处，尤其是初裂前荷载－挠度曲线斜率对弯曲韧性指数的影响一直未得到重视.JSCE－SF4标准评价方法的局限性制约了其在实际工程中的应用，ASTM C 1609 标准和CECS 13：2009标准的改进仍不足以弥补这些局限性.本文提出的SFRC 弯曲韧性评价方法弥补了现有标准评价方法的不足，能够更准确地评判SFRC在不同挠度下的弯曲韧性水平，可以较好地用于实际工程结构的弯曲韧性计算与比较.

（2）随钢纤维体积率的增加，SFRC 初始弯曲韧度比在ρf＜1.0%时有所波动，在ρf≥1.0%后总体稳定上升；随钢纤维体积率的增加，SFRC 残余弯曲韧度比总体显著提高，其中高强混凝土的增幅更大.随跨中计算挠度的增大，SFRC 残余弯曲韧度比在ρf＜1.0%时不断降低，在ρf≥1.0%后的降幅较小，能够维持较高的水平.

［1］GOPALARATNAM V S，GETTU R.On the characterization of flexural toughness in fiber reinforced concretes［J］.Cement and Concrete Composites，1995，17（3）：239－254.

［2］ASTM.ASTM C 1018 Standard test method for flexural toughness and first－crack strength of fiber reinforced concrete（using beam with third－point loading）［S］.West Conshohocken：ASTM Internation，1997：544－551.

［3］JCI.JSCE－SF4 Method of test for flexural strength and flexural toughness of fiber reinforced concrete［S］.Tokyo：Japan Concrete Institute，1984：45－51.

［4］ASTM.ASTM C 1609 Standard test method for flexural performance of fiber reinforced concrete（using beam with thirdpoint loading）［S］.Philadelphia：ASTM Internation，2006：1－8.

［5］RILEM TC 162－TDF Test and design methods of steel fiber reinforced concrete：Bending test［S］.

［6］中国工程建设标准化协会.CECS 13：2009 纤维混凝土试验方法标准［S］.北京：中国计划出版社，2010：54－59.China Association for Engineering Constructure Standardization.CECS 13：2009 Test methods used for steel fiber reinforced concrete［S］.Beijing：China Planning Press，2010：54－59.（in Chinese）

［7］中国工程建设标准化协会.CECS 38：2004 纤维混凝土结构技术规程［S］.北京：中国计划出版社，2004：58－61.China Association for Engineering Constructure Standardization.CECS 38：2004 Technical specification for fiber reinforced concrete structures［S］.Beijing：China Planning Press，2004：58－61.（in Chinese）

［8］高丹盈，刘建秀.钢纤维混凝土基本理论［M］.北京：科学技术文献出版社，1994：274－286.GAO Danying，LIU Jianxiu.Basic theory of steel fiber reinforced concrete［M］.Beijing：Scientific and Technology Documentation Press，1994：274－286.（in Chinese）

［9］朱海堂，高丹盈，谢丽，等.钢纤维高强混凝土弯曲韧性的试验研究［J］.硅酸盐学报，2004，32（5）：656－660.ZHU Haitang，GAO Danying，XIE Li，et al.Research on flexural toughness of steel fiber reinforced high－strength concrete［J］.Journal of the Chinese Ceramic Society，2004，32（5）：656－660.（in Chinese）

［10］丁一宁，董香军，王岳华.钢纤维混凝土弯曲韧性测试方法与评价标准［J］.建筑材料学报，2005，8（6）：660－664.DING Yining，DONG Xiangjun，WANG Yuehua.Testing methods and evaluating standards of flexural toughness for steel fiber reinforced concrete［J］.Journal of Building Materials，2005，8（6）：660－664.（in Chinese）

［11］秦鸿根，陆春林，孙伟.钢纤维混凝土抗弯初裂点确定方法及抗弯性能的研究［J］.混凝土及水泥制品，1991（2）：4－28.QIN Honggen，LU Chunlin，SUN Wei.Determination of the first－crack point and flexural performance of steel fiber－reinforced concrete［J］.China Concrete and Cement Products，1991（2）：4－28.（in Chinese）

［12］MINDESS S，CHEN L，MORGAN D R.Determination of the first－crack strength and flexural toughness of steel fiber－reinforced concrete［J］.Advanced Cement Based Materials，1994，1（5）：201－208.

［13］BANTHIA N，TROTTIER J F.Test methods for flexural toughness characterization of fiber reinforced concrete：Some concerns and a proposition［J］.ACI Mater J，1995，92（1）：48－57.

［14］EL－ASHKAR N H，KURTIS K E.A new simple practical method to characterize toughness of fiber－reinforced cementbased composites［J］.ACI Mater J，2006，103（1）：33－44.

［15］鞠杨，刘红彬，陈健，等.超高强度活性粉末混凝土的韧性与表征方法［J］.中国科学E辑：技术科学，2009，39（4）：793－808.JU Yang，LIU Hongbin，CHEN Jian，et al.Toughness and characterization methods of ultra high strength reactive powder concrete［J］.Science in China（Series E）：Technological Science，2009，39（4）：793－808.（in Chinese）