桥面不平顺对大跨度斜拉桥车激振动的影响

陈卫丽，王贵春

(1.郑州大学 土木工程学院，河南 郑州 450001;2.河南省建筑科学研究院有限公司，河南 郑州 450001)

近半个世纪以来，由运动车辆引起的桥梁振动问题一直受到工程师和科研人员的重视。这个问题的主要特点是车桥两个子系统之间的动力相互作用非常复杂，特别是其相互作用力不能用简单的方法确定［1］。桥梁的动力响应，依赖于车桥系统的动力特性和桥面不平顺［2］。模拟车桥系统动力相互作用的普遍方法是分别求解车辆和桥梁两个子系统的振动微分方程，而后通过迭代过程考虑其相互作用［3］。目前，科研人员已在该领域取得了一些重要成果。

G.T.Michaltsos等研究了一个具有开口截面的简支钢梁在移动荷载作用下的动力响应，分析了荷载大小、移动速度和荷载偏心等因素对钢梁动力响应的影响［4］。Y.B.Yang等用振型叠加法计算了车桥耦合振动系统的竖向动力响应，并进行了反应谱分析［5］。A.Gonzalez等考虑伸缩缝损坏以及桥面板与桥头搭板之间不均匀沉降的影响，分析了车辆通过时桥梁剪应力的动力增大问题［6］。蒋培文等分析大跨径连续梁多工况车桥耦合振动规律［7］。王贵春等对公路简支梁桥基于车桥耦合振动的冲击系数进行了研究［8］。

上述研究主要在于分析方法的建立和车桥系统耦合振动规律的探索，所采用的桥梁模型主要为梁式桥。但车桥系统的耦合振动问题十分复杂，涉及因素众多，很多问题有待于深入研究。在最近二十年，车重的增加及车速的提高以及桥梁跨度日益增大，结构形式更加复杂已导致桥梁结构动力响应的增加。分析桥面不平顺引起的大跨度桥梁的动力响应具有非常重要的理论和现实意义［9］。

在本文中，以润扬(镇江—扬州)长江公路大桥北汊斜拉桥为工程背景，研究在车桥耦合振动状态下，桥面不平顺对大跨度公路斜拉桥动力响应的影响。

1 车桥系统动力分析模型

1.1 润扬长江大桥北汊桥主桥三维有限元模型

润扬长江大桥北汊桥主桥是双塔双索面钢箱梁斜拉桥，跨径为(175.4+406.0+175.4)m。主梁采用扁平流线形钢箱梁，梁高3 m，桥面宽36.4 m。采用钢筋混凝土花瓶形塔柱，倒Y型索塔高146.9 m，钢绞线斜拉索52对。

在建立大跨度斜拉桥三维有限元动力分析模型时，对索塔、斜拉索和桥面系进行了模拟。斜拉索在自重的作用下会产生一定的垂度，引起非线性效应，利用等效弹性模量法解决这一问题。利用有限元软件ANSYS模拟桥梁结构，用梁单元模拟主梁和索塔，用杆单元模拟拉索。本文所建立的三维有限元分析模型可以考虑车桥耦合振动的多种工况。

1.2 车辆空间模型

车辆在实际行驶过程中其运行情况和自身的振动非常复杂。为便于分析作如下假定:车辆在桥上行驶时与桥面始终保持接触，不脱空;车辆沿桥作匀速运动，不考虑纵向和横向动力作用;车辆各部件对各自质心对称，且在平衡位置附近作小位移振动。

在建立车辆模型时，考虑了4个车轮的竖向位移z1～z4，车体的竖向位移zv，车体的俯仰角位移θv和车体的侧倾角位移φv共7个自由度。其中mv为车体的质量;m1～m4为4个车轮的质量(包含车悬架质量);ks1～ks4，cs1～cs4分别为车悬架刚度和阻尼;kt1～kt4，ct1～ct4分别为轮胎的刚度和阻尼，如图1所示。

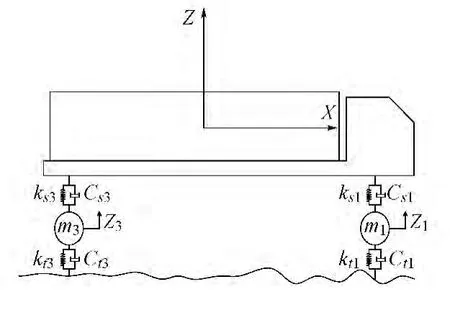
图1 车辆模型

1.3 桥面不平顺的数值模拟

设桥面不平顺与一般路面的不平顺是相同的，基于路面功率谱密度函数，利用谐波振动的线性叠加，用三角函数法将桥面不平顺模拟成均值为0的平稳高斯随机过程，并设谐波振动的相位角是随机的。则

图2为利用上述方法求得的B级桥面不平顺样本函数，由图可知，它是随机函数。图3为各级桥面不平顺最大值随桥面等级变化的曲线，显然，按着A，B，C，D级的顺序，各级桥面不平顺最大值快速增大。模拟的不平顺值可作为桥面对车辆的激励。

图2 B级桥面不平顺样本函数

2 车桥耦合振动分析方法

2.1 振动微分方程的建立

根据所建立的车辆模型，利用动力平衡原理，建立车辆振动微分方程为

图3 各级桥面不平顺最大值变化曲线

2.2 振动微分方程的求解

车辆和桥梁动力相互作用是通过车轮与桥面接触点处的位移和作用力相互影响的。在车桥耦合振动分析中，假定轮胎与桥面始终保持接触，车辆和桥梁的相互作用力大小相等，方向相反。在求解车桥振动微分方程时，利用车辆和桥梁两个子系统之间位移和力的协调条件考虑车辆与桥梁的动力相互作用，从而把振动微分方程联系起来。在计算中，采用Newmark-β法对车桥系统振动微分方程进行直接积分求解。

3 计算实例

以桥面不平顺作为车桥耦合振动的激振源，利用上述模型和计算方法，研究在车桥耦合振动作用下桥面不平顺对桥梁主跨跨中竖向动力响应、索塔塔顶纵向振动位移响应和主跨最外侧拉索动应力响应的影响。在计算中，假定车辆沿偏离桥梁中心线3 m的位置运行，车辆行驶速度为20 m/s，车辆质量为20 t，桥面等级分别为国家标准A～D级。

3.1 桥梁主跨跨中竖向振动位移

图4为在A，D级桥面情况下主跨跨中竖向振动位移时程曲线。从图中可以看出，在D级桥面情况下，振动位移幅值远大于其在A级桥面情况下的幅值。图5为主跨跨中竖向振动位移最大值随桥面等级变化的情况。由图可知，随着桥面不平顺状况的变差，主跨跨中振动位移最大值逐渐增加。在B，C，D级桥面情况下，主跨跨中竖向振动位移最大值分别是A级的1.89，5.10和12.17倍。由此可知，随着桥面不平顺状况变差，振动趋于强烈。

图4 主跨跨中振动位移时程曲线

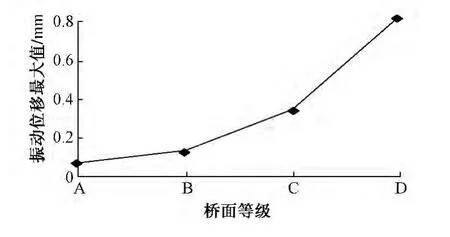
图5 主跨跨中振动位移最大值变化曲线

3.2 桥梁主跨跨中动内力

图6为在A，D级桥面情况下主跨跨中动弯矩时程曲线。从图中可以看出，在D级桥面情况下，振动弯矩幅值远大于其在A级桥面情况下的幅值。图7为主跨跨中动弯矩最大值随桥面等级变化的情况。由图可知，随着桥面不平顺状况的变差，主跨跨中动弯矩最大值逐渐增加。在B，C，D级桥面不平顺情况下，主跨跨中动弯矩最大值分别是 A级的3.47，7.92和11.98倍。

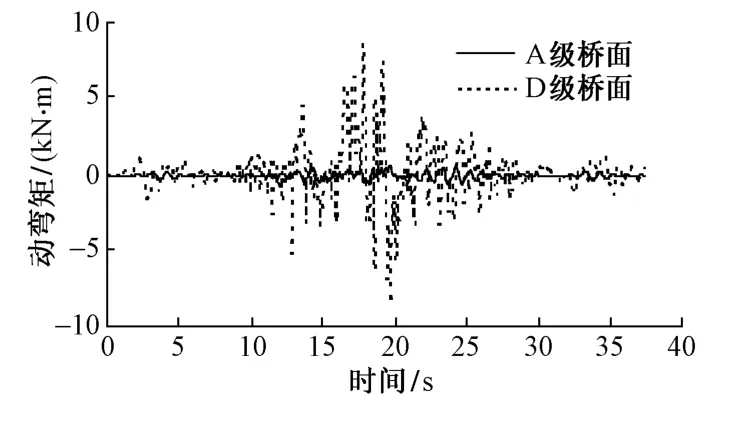
图6 主跨跨中动弯矩时程曲线

图7 主跨跨中动弯矩最大值变化曲线

图8 跨中节点动剪力时程曲线

图9 主跨跨中动剪力最大值变化曲线

图8为在A，D级桥面情况下主跨跨中动剪力时程曲线。从图中可以看出，在D级桥面情况下，动剪力幅值远大于其在A级桥面情况下的幅值。图9为主跨跨中动剪力最大值随桥面等级变化的情况。由图可知，随着桥面不平顺状况的变差，主跨跨中动剪力逐渐增加。在B，C，D级桥面不平顺情况下，主跨跨中动剪力最大值分别是A级的2.13，4.35，9.47倍。

由上述讨论可知，随着桥面状况变差，斜拉桥主梁跨中的动弯矩和动剪力均明显增加，桥面状况越差，增加的幅度越大，振动越剧烈。

3.3 桥梁索塔塔顶纵向振动位移

图10为在A，D级桥面情况下桥梁索塔塔顶纵向振动位移时程曲线。从图中可以看出，在D级桥面情况下，振动位移幅值远大于其在A级桥面情况下的幅值。图11为索塔塔顶纵向振动位移最大值随桥面等级变化的情况。由图可知，随着桥面不平顺状况的变差，索塔塔顶纵向振动位移最大值逐渐增加。在B，C，D级桥面不平顺情况下，索塔塔顶纵向振动位移最大值分别是A级的2.40，7.03和9.47倍。但总体来看，索塔塔顶纵向振动幅度不大。

3.4 桥梁主跨最外侧拉索动应力

图10 索塔塔顶纵向振动位移时程曲线

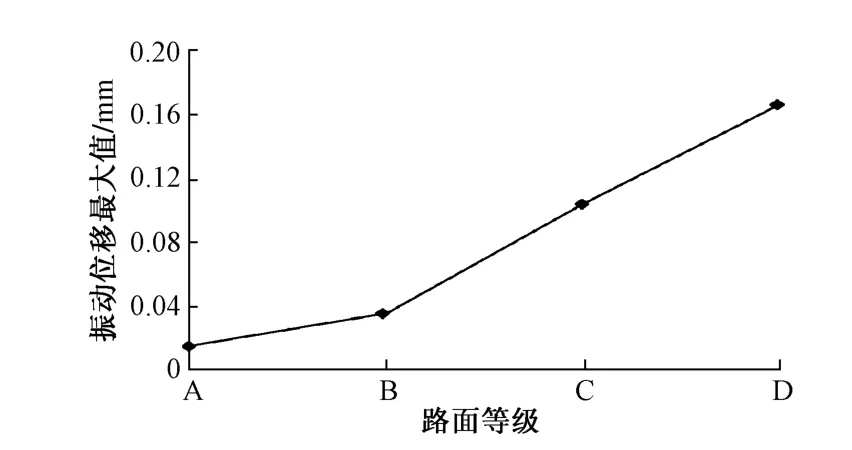
图11 索塔塔顶纵向振动位移最大值变化曲线

图12为在A，D级桥面情况下桥梁主跨最外侧拉索动应力时程曲线。从图中可以看出，在D级桥面情况下，动应力幅值远大于其在A级桥面情况下的幅值。图13为桥梁主跨最外侧拉索动应力最大值随桥面等级变化的情况。由图可知，随着桥面不平顺状况的变差，拉索动应力最大值逐渐增加。在B，C，D级桥面不平顺情况下，拉索动应力最大值分别是A级的2.49，7.00和13.28倍。跨中附近拉索的动应力受桥面不平顺影响较大，桥面不平顺越严重，影响越显著。

图12 拉索动应力时程曲线

图13 拉索动应力最大值变化曲线

4 结论

1)数值模拟结果表明，从A级至C级桥面，不平顺最大值是近似成几何级数增加的。从C级至D级桥面，不平顺最大值增加的程度有所减缓。D级桥面最大不平顺值可达10 cm左右。

2)主跨跨中竖向振动位移、动弯矩和动剪力均随桥面不平顺的增加而逐渐增大，且其增大趋势越来越明显。其中动弯矩增幅与其他二者相比略显平缓。

3)随着桥面不平顺状况的变差，索塔塔顶纵向振动位移最大值逐渐增加。但总体来看，索塔塔顶纵向振动幅度不大。

4)主跨最外侧拉索动应力随桥面不平顺的增加而逐渐增大，其中当桥面不平顺等级由B级变到C级时，其增大程度最为明显。

［1］WYSS J C，SU D，FUJINO Y.Prediction of vehicle-induced local responses and application to a skewed girder bridge［J］.Engineering Structures，2011，33(4):1088-1097.

［2］MOGHIN H，RONAGH H R.Development of a numerical model for bridge-vehicle interaction and human response to traffic-induced vibration［J］.Engineering Structures，2008，30(12):3808-3819.

［3］OLIVA J，GOICOLEA J M，ANTOLIN P，et al.Relevance of a complete road surface description in vehicle-bridge interaction dynamics［J］.Engineering structures，2013，35(6):466-476.

［4］MICHALTSOS G T，SARANTITHOU E，SOPHIANOPOULOS D S.Flexural-torsional vibration of simply supported open crosssection steel beams under moving loads［J］.Journal of sound and vibration，2005，284(3-5):479-494.

［5］YANG Y B，LIN C W.Vehicle-bridge interaction dynamics and potential applications［J］.Journal of sound and vibration，2005，284(1-2):205-226.

［6］GONZALEZ A，CANTERO D，OBRIEN E J.Dynamic increment for shear force due to heavy vehicles crossing a highway bridge［J］.Computers ＆ Structures，2004，89(23-24):2261-2272.

［7］蒋培文，贺拴海，宋一凡，等.大跨径连续梁多工况车桥耦合振动规律分析［J］.武汉理工大学学报，2011，33(7):62-67.

［8］王贵春，章长玖，陈淮.公路简支梁桥在车桥耦合作用下的冲击系数研究［J］.铁道建筑，2011(9):20-23.

［9］陈卫丽.大跨度公路斜拉桥车桥耦合振动分析［D］.郑州:郑州大学，2013.