递减步长果蝇优化算法及应用

宁剑平，王 冰，，李洪儒，许葆华

1)广州军区76127部队，湖南郴州424202;2)军械工程学院，石家庄050003

支持向量机 (support vector machine，SVM)［1-2］是一种基于统计学理论的机器学习算法，该算法利用VC维 (Vapnik-Chervonenkis dimension，VC维)理论和结构风险最小化原则，研究小样本下模型的泛化能力，具有理论完备性好、适应性强、全局优化及泛化性能好等优点.SVM的性能主要取决于核函数和参数的选取，如何根据实际问题选择合适的核函数和参数是关键.但该问题目前还缺乏理论指导［3］.当前常见的参数寻优方法包括梯度下降算法、遗传算法和粒子群优化算法［4］都存在缺陷.梯度下降法效率低，稳定性不高［5］;遗传算法收敛速度慢，容易陷入局部最优值［6］;粒子群优化算法较遗传算法收敛速度快也更易于实现，但容易陷入局部最优，局部搜索能力较差.

果蝇优化算法 (fruit fly optimization algorithm，FOA)是2011年潘文超提出的一种根据果蝇觅食行为推演出的寻求全局优化的群智能方法.该算法通过嗅觉搜索提高果蝇个体的多样性，增大果蝇个体的搜索空间，通过视觉搜索使果蝇个体快速收敛.该算法具有参数少、计算速度快、全局寻优能力强和易于实现等特点，现已在许多领域得到了有效的研究与应用［7-10］.

本研究针对果蝇优化算法中固定步长对于搜索效率敏感，且不易选取的问题，提出一种递减步长果蝇算法 (diminishing step fruit fly optimization algorithm，DS-FOA)，将固定步长改为依觅食进程递减.运用该算法优化SVM回归模型的惩罚因子c与核函数参数g，选取样本数据进行预测分析，并将该算法与FOA、粒子群优化 (particle swarm optimization，PSO)算法和遗传算法 (genetic algorithm，GA)进行性能对比.

1 算法原理

1.1 果蝇算法原理［11］

FOA首先随机初始化果蝇群体的位置坐标，根据群体的位置随机初始化群体中的果蝇利用嗅觉搜索食物的随机方向和距离.由于无法得知食物的位置，因此先估计果蝇与原点的距离，以距离的倒数做为当前的味道浓度判定值，以此判定值得到每个果蝇个体的味道浓度.保留最佳味道浓度值和果蝇最佳个体位置，果蝇群体即利用视觉往该位置飞去.在新的最佳位置重新初始化群体果蝇位置，并重复上述过程，直到找到最优的食物位置为止.FOA步骤如下:

1)在设定区间随机初始化果蝇群体位置坐标(x，y).

2)根据果蝇群体位置坐标，采用式(1)初始化群体中果蝇个体的位置坐标，使该个体果蝇利用嗅觉搜寻食物.

其中，Lr为在固定步长区间［－L，L］内随机生成的步长值，可由Lr=L×rands(1，1)求得，L为果蝇个体利用嗅觉搜索的固定步长值.

3)由于果蝇群体无法得知食物位置，因此需先采用式(2)估计第i个果蝇个体与坐标原点的距离di，再按照式(3)计算味道浓度判定值Si.

4)将Si代入味道浓度判定函数 (fitness function)中，得到该果蝇个体利用嗅觉得到的味道浓度为

5)找出果蝇群体中味道浓度最高的个体，即

其中，bestsmell为最高的味道浓度;bestindex为果蝇群体中具有最高味道浓度的果蝇个体序号;smell为果蝇群体的味道浓度集合.

6)判断味道浓度是否优于前一代的浓度，若是，则执行7);否则，重复执行2)至6).

7)利用式 (6)和式 (7)保留最佳味道浓度值与最佳果蝇个体的位置坐标，使果蝇群体利用视觉向该位置飞去.

8)判断是否达到结束条件 (通常根据实际问题设至固定适应度值或最大迭代代数)，若是，则找到最优食物位置;否则，执行2).

1.2 递减步长果蝇算法

在FOA步骤2)中，步长L设为固定值，即在每次觅食迭代中，果蝇个体利用嗅觉在果蝇群体位置周围以步长值为单位，随机搜索.显然，在果蝇群体个数一定的情况下，步长越大，果蝇个体的搜索空间越大，全局搜索能力越强，但其局部寻优能力会降低;反之，若步长过小，则果蝇个体的局部寻优能力较强，搜索空间较小，全局搜索能力较弱，果蝇个体容易陷入局部最优.可见，在FOA中，步长参数的选取直接影响算法的执行效率.因此，运用果蝇算法解决实际问题时，必须选择合适的步长值，使之既有较强的全局搜索能力以免陷入局部最优，又具有较好的局部寻优能力，以提高搜索的精度.

本研究通过分析模拟实验结果，基于果蝇算法，变固定补偿为递减补偿，提出DS-FOA算法，并设步长值为

其中，L0为初始步长值;Gmax为最大觅食迭代数;G为当前觅食代数.

当第1代果蝇觅食时，L=L0，果蝇个体步长为最大值L0.果蝇觅食迭代每增加1代，步长减小L0/Gmax，直至最后一代减至L0/Gmax.

显然，DS-FOA在迭代初期具有最大的搜索步长，此时，搜索空间大，全局寻优能力最强.随着觅食迭代次数的增加，算法的局部搜索能力逐渐增强，保证了觅食初期有较大概率找到全局最优解，却不致于陷入局部最优，觅食末期能达到最大的搜索精度，从而实现全局搜索能力和局部寻优能力的平衡.

1.3 模拟验证

为验证DS-FOA的寻优效果，以正弦变化率函数为例进行模拟分析，如式(9).

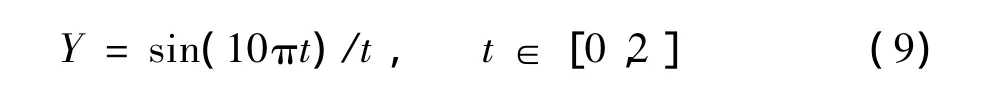
该函数的特点是在定义域内具有一个最小值和多个局部极小值，对应的函数曲线如图1.

图1 正弦变化率函数曲线Fig.1 Curve of sine gradient function

分别选用固定步长为3和30的FOA以及初步长为30的DS-FOA进行最小值寻优，参数设置见表1.按照果蝇算法规则，将自变量定义为

表1 模拟实验参数设置Table 1 Algorithm parameter setting in contrast experiment

经觅食迭代后，3种模拟实验的最优值觅食曲线及果蝇飞行轨迹分别见图2、图3和图4.

由模拟分析可见，DS-FOA算法在觅食初期，由于搜索范围的最大化，全局寻优能力强，第1代即达到较优值－6.748;随着觅食迭代次数的增加，算法结果逐渐接近最优值，觅食末期，随着局部搜索能力的增强，还有轻微的最优值调整;最后在第48代处达到最优值－6.825，由该果蝇个体的觅食路线也可观察到果蝇群体由稀疏到稠密的进化过程;L=30时，FOA的全局搜索能力强，在第7代即达到最优值－6.824，但之后一直不变.可见，固定的搜索尺度导致大步长FOA在迭代后期局部搜索能力不强，果蝇个体在(［－20，20］，［－20，20］)的直角坐标系范围内呈近似均匀分布状态，全局搜索能力强，而局部搜索能力不足;当L=3时，果蝇在第17代达到最优值－2.869.可见，由于小步长导致算法局部搜索能力强，全局搜索能力弱，使算法过早地陷入局部最优值.果蝇个体在(［－4，0］，［－2，4］)的直角坐标范围内呈均匀搜索状态，搜索空间过小，无法跳出局部最优解.

综上研究认为，DS-FOA保持了搜索过程中的搜索尺度变化，平衡了算法的全局与局部搜索能力，对于寻优问题取得较好效果.

图2 DS-FOA效果Fig.2 (Color online)Course of DS-FOA

图3 L=30时FOA效果Fig.3 (Color online)Course of FOA for L=30

2 实例分析

2.1 数据选择与处理

为考察DS-FOA优化算法的应用效果，运用该算法优化SVM模型惩罚因子参数c和核函数参数g.采集大智慧证券软件1997-10-22到2009-08-19记录的上证指数作为实验测试数据.该样本数据是一个2 079×6的矩阵，记录了此时间段内的2 079个交易日每日上证综合指数的6种指标.假设当日开盘指数为因变量，前一日6种指标值为自变量.选取前2 069组数据为SVM训练样本，后10组数据作为检测SVM回归模型性能的验证样本.

由于样本向量中各指标的数量级差别较大，为便于计算并减小误差，采用式(12)对输入样本进行归一化处理，而对SVM模型的输出则进行反归一化处理，即式(12)的逆运算，如此便可得到实际预测数据.

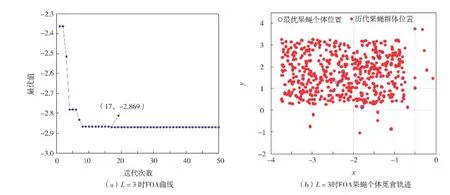
图4 L=3时FOA效果Fig.4 (Color online)Course of FOA for L=3

其中，Xmax和Xmin分别为辅助变量X的上下限值.本研究取 Xmax=2，Xmin=1.

2.2 SVM回归模型参数优化效果及评测

基于训练样本数据，分别运用DS-FOA、FOA、PSO［12-13］和 GA［14］对 SVM 回归模型参数 c 和 g 进行优化.每种算法进行10组实验.SVM的参数训练采用K-CV方法，本研究取K=3.这4种优化算法均以训练样本最低均方误差作为个体适应度值，主要参数设置如表2.

图5为典型的第5组算法寻优进化曲线对比图，表3为4种算法10组实验优化结果的定量对比.由分析可见，DS-FOA的寻优精度最高，且运行时间最短，因此，搜索效率最高;FOA运行时间与DS-FOA相近，但由于局部寻优能力较低，导致寻优精度略低;PSO与GA优化算法的运行速率远低于DS-FOA与FOA，而前两者相比，PSO的寻优精度较高，GA则由于过早收敛而陷入局部最优，寻优精度最低.可见，DS-FOA在保持FOA的优势前提下，进一步提高了算法的寻优精度和搜索效率.

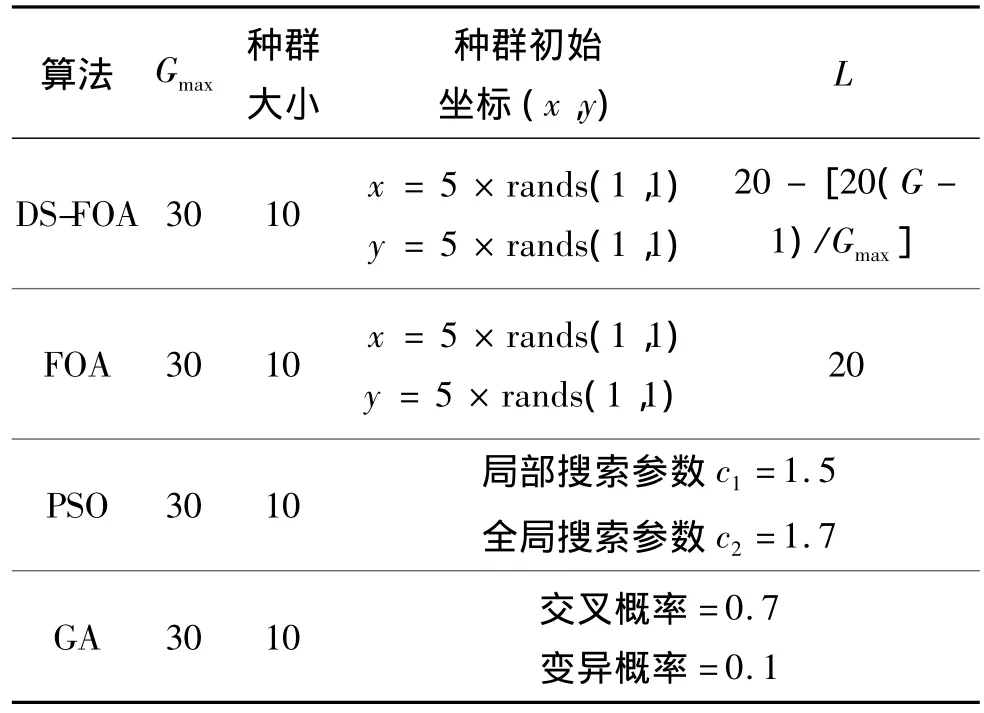
表2 对比实验算法参数设置Table 2 Algorithm parameters setting in contrast experiments

2.3 SVM回归效果及评测

以第5组实验结果为依据，建立SVM回归模型，对10组验证样本数据进行回归分析，检验并对比4种SVM回归模型性能，各模型的预测结果见表4.

图5 实例分析中算法适应度曲线Fig.5 Adaption curves of experiment algorithms

表3 四种算法10组实验优化结果对比Table 3 Contrast of algorithm optimization in ten tests

表4 四种SVM模型算法预测结果Table 4 Forecast results of four kinds of SVM model

图6和表5分别描述了4种SVM回归模型的预测结果曲线和预测效果.可见，经由DS-FOA优化参数的SVM回归模型均方误差达2.29×10－5，相关系数达98.9221%，在4种优化算法中，效果均达到最优值，与FOA相比，DS-FOA的优化性能有明显提高.

表5 四种算法预测效果对比Table 5 Contrast of four algorithm forecast effects

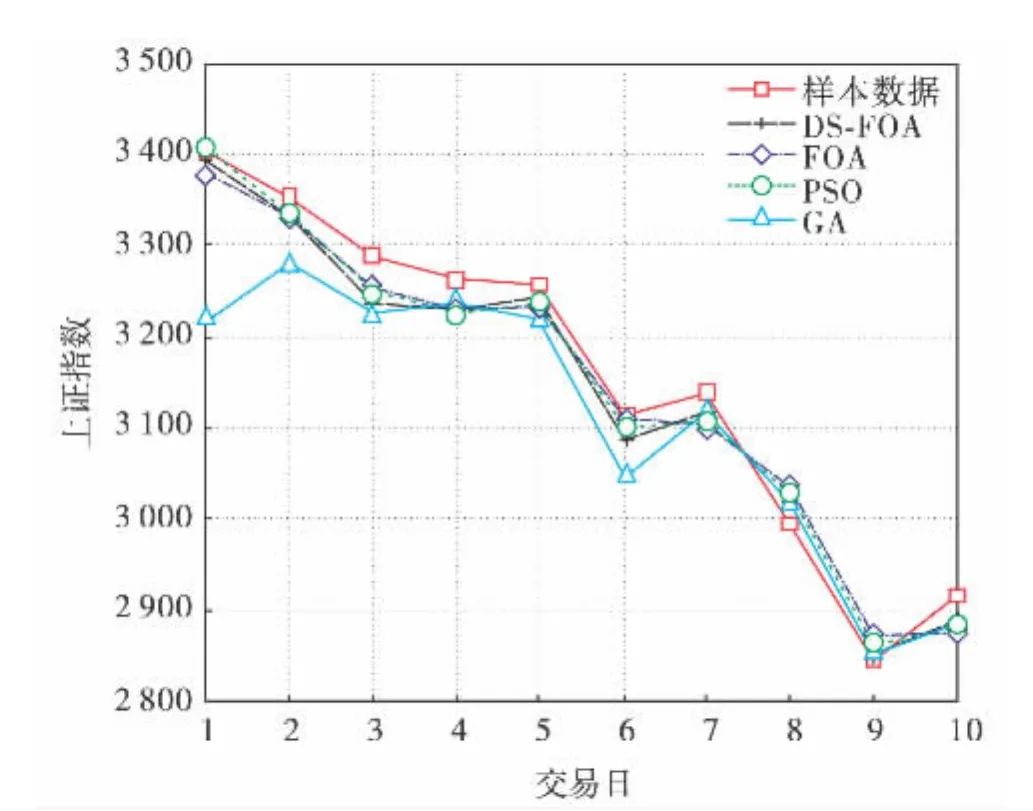
图6 四种算法预测曲线对比Fig.6 (Color online)Forecast curves of four algorithms

结 语

针对实际问题中果蝇优化算法 (FOA)步长参数对寻优效率影响权重大、不易选取的不足，提出递减步长果蝇优化算法 (DS-FOA).该算法实现了全局搜索能力和局部寻优能力的平衡，使果蝇群体伴随觅食行为进程，实现全局搜索能力和局部寻优能力的此消彼长.将DS-FOA应用到SVM模型的参数优化中，仿真结果表明，其搜索效率、预测精度和运算速度均取得较好效果.与FOA、PSO和GA算法相比，DS-FOA优化参数的SVM回归模型的均方误差最低，回归效果好.

/References:

［1］ Vapnik V N.The nature of statistical learning theory［M］.New York(USA):Springer-Verlag，1995.

［2］ Cortes C，Vapnik V N.Supporter vector networks［J］.Machine Learning，1995，20(3):273-297.

［3］ Chapelle O，Vapnik V，Bousquet O，et al.Choosing multiple parameters for support vector machines ［J］.Machine Learning，2002，46(1):131-159.

［4］ Zhu Fengming，Fan Minglong.Chaos particle swarm optimization algorithm for optimizing the parameter of SVM［J］.Computer Simulation，2010，27(11):183-186.(in Chinese)朱凤明，樊明龙.混沌粒子群算法对支持向量机模型参数的优化 ［J］.计算机仿真，2010，27(11):183-186.

［5］ Zhou Xiaojian，Ma Yizhong，Liu Liping，et al.Gradientenhanced least squares support vector regression ［J］.Journal of Nanjing University of Science and Technology Natural Science，2011，35(1):138-143.(in Chinese)周晓剑，马义中，刘利平，等.基于梯度信息的最小二乘支持回归机 ［J］.南京理工大学学报自然科学版，2011，35(1):138-143.

［6］ Chen Tao，Yong Longquan，Deng Fang'an，et al.Parameters selection of support vector machine based on differential evolution［J］.Computer Engineering and Applications，2011，47(5):24-26.(in Chinese)陈 涛，雍龙泉，邓方安，等.基于差分进化算法的支持向量机参数选择 ［J］.计算机工程与应用，2011，47(5):24-26.

［7］ Zhang Xiang，Chen Lin.Fault diagnosis based on support vector machines optimized by fruit fly optimization algorithm ［J］.Electronic Design Engineering，2013，21(16):90-93.(in Chinese)张 翔，陈 林.基于果蝇优化算法的支持向量机故障诊断 ［J］.电子设计工程，2013，21(16):90-93.

［8］ Cheng Hui，Liu Chengzhong.Mixed fruit fly optimization based on chaotic mapping ［J］.Computer Engineering，2013，39(5):218-221.(in Chinese)程 慧，刘成忠.基于混沌映射的混合果蝇优化算法［J］.计算机工程，2013，39(5):218-221.

［9］ Wang Xuegang，Zou Zaojian.FOA-based SVM parameter optimization and its application in ship manoeuvring prediction ［J］.Journal of Shanghai Jiaotong University，2013，47(6):884-888.(in Chinese)王雪刚，邹早建.基于果蝇优化算法的支持向量机参数优化在船舶操纵预报中的应用［J］.上海交通大学学报，2013，47(6):884-888.

［10］ Zhou Ping，Bai Guangchen.Robust design of turbineblade low cycle fatigue life based on neural networks and fruit fly optimization algorithm ［J］.Journal of Aerospace Power，2013，28(5):1013-1018.(in Chinese)周 平，白广忱.基于神经网络与果蝇优化算法的涡轮叶片低循环疲劳寿命健壮性设计［J］.航空动力学报，2013，28(5):1013-1018.

［11］ Pan W T.A new fruit fly optimization algorithm:taking the financialdistress modelas an example ［J］.Knowledge-Based Systems，2012，26(1):69-74.

［12］ Tang Jun.Principle of particle swarm optimization algorithm and applications in civil engineering［J］.Computer＆ Digital Engineering，2009，37(10):153-156.(in Chinese)唐 俊.微粒群算法原理及改进算法在土木工程中应用［J］.计算机与数字工程，2009，37(10):153-156.

［13］ Wang Huadong，Li Wei.Study on logistics distribution route optimization by improved particle wwarm optimization［J］.Computer Simulation，2012，29(5):243-246.(in Chinese)王华东，李 薇.粒子群算法的物流配送路径优化研究 ［J］.计算机仿真，2012，29(5):243-246.

［14］ Yao Jinbao，Yao Baozhen，Yin Zhihong，et al.A bus headway optimization model with dual-population genetic algorithm ［J］.Journal of Shenzhen University Science and Engineering，2012，29(6):559-564.(in Chinese)姚锦宝，姚宝珍，尹智宏，等.基于双种群遗传算法的公交线路发车间隔优化 ［J］.深圳大学学报理工版，2012，29(6):559-564.