风障对大跨度悬索桥静风稳定性的影响
杜 飞 (中国市政工程中南设计研究总院有限公司,湖北 武汉 430010)
0 前 言
目前世界桥梁工程步入了建设跨海连岛工程的新时期,已有且将有多座大跨度桥梁建于强(台)风多发地区。强(台)风会对桥面行车安全性和舒适性产生不利影响[1-4]。作为改善桥面行车风环境的主要手段,风障被广泛采用,如中国杭州湾大桥、香港青马大桥、法国Millau桥、英国Severn悬索桥、Queen Elizabeth二桥和Severn二桥等[1]均加设了风障。目前关于风障的研究主要集中在风障对桥面行车风环境改善效果的影响。Smith[5]等研究了风障空隙率与挡风效果的关系。陈晓冬[1]、Charuvisita[6]等对桥塔区局部风障的挡风效果进行了深入研究。仅有少量文献涉及风障对大跨度桥梁抗风性能的影响。Smith等[5]认为风障对桥梁结构带来了非常大的气动阻力荷载,并且推测可能引起桥梁动力稳定性的下降。Ostenfeld[7]通过风洞试验证明透风率在40%~50%之间的风障既能够提供足够的挡风效率,又限制了气动阻力的增幅和稳定性的下降。Reinhold等[8]在丹麦大海带桥风洞试验研究中提出的风障措施最后因抗风稳定性问题而未被采用。
为了研究风障对大跨度悬索桥静风稳定性的影响,本文以某大跨悬索桥为研究背景,在风洞试验获得的主梁静力三分力系数的基础上,对比研究了透风率50%的风障静风稳定性的影响。
1 工程概况及计算模型
某悬索桥跨径布置为578m+1650m+485m=2713m,如图1所示。加劲梁断面采用全宽36m的分体双箱梁,中间开槽宽度为6m,梁高3.5m。钢筋混凝土桥塔塔柱采用矩形凹角断面,塔高约为200m,桥面以上部分塔高165m。该桥位于亚热带季风性海洋气候区域,桥址处基本风速为41.1m/s,成桥状态桥面基准风速高达55.14 m/s。

图1 某悬索桥立面图(单位:mm)
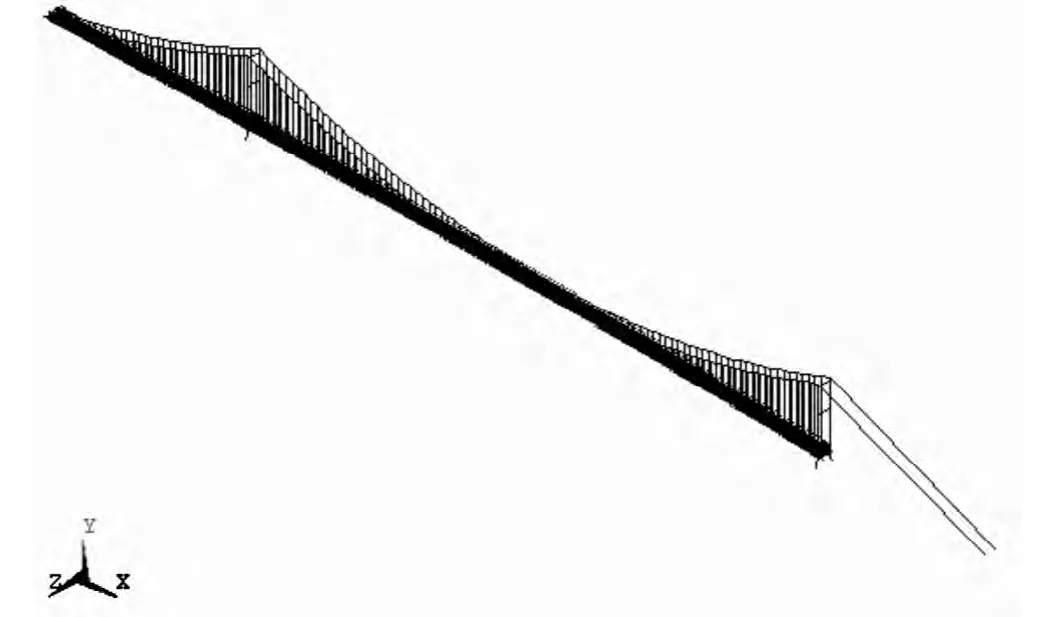
图2 有限元模型图

图3 静力三分力系数
由于该桥采用分体双箱梁,对其建立有限元模型时采用双主梁模型,其中,加劲梁、桥塔用三维梁单元模拟,主缆和吊杆模拟为只承受拉力的杆单元,并计入主缆和吊杆的初始应变。由于主缆单元划分较细,不必考虑其垂度效应影响。为了便于施加风荷载和提取主梁扭转位移,在加劲梁形心处增设一道虚拟主梁。有限元模型如图2所示。
图3为风洞试验中测得的成桥状态风轴加劲梁断面静力三分力系数,试验中采用的风障对应实桥高度是3m,透风率为50%。
2 分析原理及方法
考虑到结构的变形,静力三分力系数可描述为有效风攻角a的函数,而有效风攻角a 是初始风攻角θ0与由静风荷载引起的加劲梁扭转变形产生的附加攻角θ 之和[10]。由于加劲梁扭转变形通常沿桥跨方向是变化的,因而作用在加劲梁上的静力三分力也是空间变形的函数。
要考虑静风作用下的非线性影响,最重要的问题是要决定非线性变形及空气静力引起的桥梁结构变形状态[11]。考虑空气静力非线性影响的结构增量迭代静力平衡方程为:

3 计算结果及分析
大气边界层中强风的攻角可能有-3°~+3°范围的微小变化[9],因此分别选取初始攻角为-3°、0°和+3°,以结构只承受恒载为初始状态,分别利用不加设风障和加设风障时的静力三分力系数,对该悬索桥进行了非线性静风稳定的全过程分析。计算中以10 m/s为初始风速步长,随着风速的增大适时调整风速步长以搜索结构的临界失稳风速。
该悬索桥各初始风攻角下的静风失稳临界风速如表1所示。从表中可知,最低临界风速为108.2 m/s,大于检验风速66.17 m/s,因此无论是否加设风障,该悬索桥均具有较好的静风稳定性。初始攻角为-3°和0°时,有风障时的静风失稳临界风速大于无风障时的静风失稳临界风速;而在初始攻角为+3°时,有风障时的静风失稳临界风速仅略小于无风障时的静风失稳临界风速。

静风失稳临界风速(m·s-1) 表1
图4所示为该悬索桥在0°初始攻角下主梁跨中位移随风速变化全过程。由图中曲线可见,随着风速的逐级增长,结构的竖向位移、横向位移和扭转角总体呈非线性增长,达到临界风速时,位移出现发散,表明结构已经在静风力和恒载作用下丧失稳定性。因此,该桥的静风变形过程是主梁竖弯、侧弯和扭转变形耦合发展的过程。失稳形态为空间弯扭耦合失稳,竖向位移、横向位移和扭转变形耦合在一起。考察该悬索桥的静风失稳过程可知,其失稳是由结构的初始平衡状态开始,随静风速的增加,结构的姿态发生改变,其中的扭转变形引起风与结构之间的有效攻角不断增大,三分力系数亦随之发生变化,从而导致作用于结构上的静风荷载随风速增长呈非线性发展,进而结构变形随风速的增加也各自呈现出不同程度的非线性特征,如横向位移随风速变化曲线的非线性程度小于竖向位移和扭转角。
从图4(a)可以看到,在相同风速下,有风障时主梁跨中横向位移大于无风障时主梁跨中横向位移。这是由于在很大的攻角范围内,有风障时阻力系数大于无风障时阻力系数。

图4 初始攻角0°时主梁跨中位移随风速变化曲线
无风障时,扭转角随风速的增长而增长(图4(c)),而竖向位移经历了一个先略微递减而后递增的过程(图4(b))。这是由于,在初始状态下主梁的扭转角为0,即初始有效攻角为0°,考察图3可知,在有效攻角随风速变化的整个过程中,无风障时升力矩系数始终为正值,而升力系数由负值向正值转变。该悬索桥升力力系数的这一特殊变化规律导致了竖向位移的发展历程具有特殊性。
有风障时,在0~140m/s风速范围内有效攻角随风速的增长而减小,对应的升力矩系数始终负值,且随着有效攻角的减小而减小,因此扭转角随风速的增长而减小。升力系数和升力矩系数有相同的变化规律,因此在0~80m/s风速范围内竖向位移随风速增长而减小。但是在80~125m/s风速范围内,随着主梁横向位移增大,吊杆内力也随之增大,吊杆对主梁向上的提升力作用超过了向下的静风升力作用,因此竖向位移随风速增长而增大。当风速超过125m/s时,主梁扭转角(或有效攻角)急剧减小,升力矩系数相应减小,向下作用的静风升力快速增大,超过了吊杆对主梁向上的提升力作用,因此在125~140m/s风速范围内竖向位移又经历了一个随风速增长而减小的过程。
在0°初始攻角下,有风障时始终向下作用的升力使拉索的垂度效应减小,增加了结构的重力刚度,结构的整体切线刚度因此而增加[12],尤其扭转刚度的增加是在开始加载阶段扭转变形增长速度较小(图4(c))的主要原因,也是有风障时静风失稳临界风速大于无风障时静风失稳临界风速的主要原因。
综上所述,加设透风率为50%的风障不会降低大跨度悬索桥的静风稳定性,在某种程度上抑制了静风失稳。
4 结 论
基于某悬索桥有无风障风洞测力试验获得的加劲梁三分力系数,进行非线性静风稳定对比分析,可得出关于风障(透风率50%)的如下结论:
①风障不会降低大跨度悬索桥的静风稳定性,在某种程度上抑制了静风失稳,尤其是在负攻角和零攻角时;
②在相同风速下,有风障时主梁跨中横向位移大于无风障时主梁跨中横向位移,这是由于在很大的攻角范围内,有风障时阻力系数大于无风障时的阻力系数。
[1]陈晓冬.大跨桥梁侧风行车安全分析[D].上海:同济大学,2007.
[2]Gawthorpe R G.Wind effects on ground transportation[J].Journal of Wind Engineeringand Industrial Aerodynamics,1994,52(1).
[3]Baker CJ.The problems of road vehicles in cross winds[J].Journal of Highways Transport,1991,38(5).
[4]Maruyama Y,Yamazaki F.Driving Simulator Experiment on the Moving Stability of an Automobile Under Strong Crosswind[J].Journal of Wind Engineeringand Industrial Aerodynamics,2006,94(4).
[5]Smith B W,Barker C P.Design of wind screens to bridges,experience and applicationson major bridges[J].Bridge Aerodynamics,1998.
[6]Charuvisita S,Kimurab K,Fujino Y.Effectsof wind barrier on a vehicle passing in the wake of a bridge tower in cross wind and its response[J].Journal of Wind Engineeringand Industrial Aerodynamics,2004,92(7).
[7]Ostenfeld K H.Denmarks Great Belt Link[C].The 1989 ASCE Annual Civil Engineering Convention,New Orleans,1989.
[8]Reinhold T,Larsen A,Damsgaard A,et al.Wind tunnel testingfor the great belt east suspension bridge[C].Proceedings of the Symposium on Structural Engineeringin Natural Hazards Mitigation,1993.
[9]项海帆,林志兴.公路桥梁抗风设计指南[M].北京:人民交通出版社,1996.
[10]Boonyapinyo V,Lauhatanon Y,Lukkunaprasit P.Nonlinear aerostatic stability of suspension bridge[J].Engineering Structures,2006,28(5).
[11]项海帆,葛耀君.悬索桥跨径的空气动力极限[J].土木工程学报,2005,38(1).
[12]韩大建,邹小江.大跨度斜拉桥非线性静风稳定分析[J].工程力学,2005,22(1).

