基于多分类器组合的高光谱图像波段选择方法

李士进，常纯，余宇峰，王亚明

(河海大学计算机与信息学院，江苏南京210098)

随着遥感技术和成像光谱仪的发展，高光谱图像的分辨率不断提高，应用需求越来越广泛，但其波段数多、数据量庞大等特点给高光谱图像的分类、识别等带来了很大的困难。利用全部波段数据进行分类等处理不但处理困难，而且由于大量冗余信息的存在和部分噪音波段或信噪比很低的波段数据的影响还会降低分类或识别精度[1]。因此，在保证地物识别率的情况下，进一步挖掘发现具有鉴别信息的波段，减少数据量、节省计算资源的降维处理非常必要。特征提取和特征选择是高光谱图像的2种主要降维方法。由于高光谱图像的每一个波段都对应着一幅相应波段的图像，通过线性或非线性变换，将高维特征空间映射到低维空间的特征提取的方法会使提取出来的特征失去原有的物理意义，所以特征提取的方法并不适用于高光谱图像的降维。而波段选择是从高光谱图像所有波段中选择最具鉴别力的波段子集，既能大大降低高光谱图像的数据维数，又能比较完整地保留分类鉴别信息，是目前高光谱降维处理的主流方法[2，3－11]。

针对高光谱波段选择问题，研究人员提出了各种方法。Serpico等提出了一种局部极值约束的离散二进制空间搜索方法用于高光谱波段选择[2]。后来，Serpico等继续开展了研究[12]，提出了针对分类正确率最优化的连续波段选择方法，他们把若干相邻波段进行平均，提出了s－bands的概念。该方法取得了较高的分类正确率，但这是一种特征提取和波段选择的混合算法，涉及的波段数远大于一般方法所选择的波段。Bazi等提出了基于遗传算法和支持向量机的高光谱波段选择方法[4]，在搜索最佳鉴别波段过程中，同时对SVM参数进行了优化。Sotoca等提出了基于确定性去火的随机搜索方法用于波段选择[5]，在搜索过程中，他们尽可能地考虑了波段之间的无关性。Guo等[6]发现特征选择时只保留与类别信息最相关的波段存在一定的问题，特别是特征之间相关性较大时更加严重。他们提出了一种快速的贪心优化策略进行波段选择，但从最终的分类结果看不是很理想。戴宏亮与戴道清[7]提出了智能遗传算法同时优化全间隔自适应模糊支持向量机参数集和波段选择中的大量参数，构成一种智能分类器，进行高光谱遥感图像分类。吴昊等[8]将分组的概念引入波段选择中，利用条件互信息将波段分成若干组，再使用支持向量机和遗传算法相结合的搜索算法(GA－SVM)搜索出相对最优的波段组合。Yang等提出了最小估计丰度协方差(MEAC)的波段选择方法[9]，在选择过程中估计候选波段与已经选择波段的丰度协方差矩阵的迹。葛亮等为使无监督的波段选择能够更好地保留高光谱图像的鉴别信息，提出一种基于波段聚类的高光谱图像波段选择方法[10]。王立国与魏芳洁提出一种结合遗传算法和蚁群算法的高光谱图像波段选择方法[11]。该算法首先利用遗传算法以较快的寻优能力获得几组较优解，以此来初始化蚁群算法的初始信息素列表，然后用蚁群算法以较高的求精解能力获得最优波段组合。Li等[12]将时间序列模式匹配的思想运用到高光谱波段选择中，先通过提取光谱曲线中重要点作为候选波段集，然后再利用分支定界法搜索最优波段子集。

虽然目前高光谱波段选择的方法很多，但由于原始波段数目一般高达数百个，以往基于搜索算法的波段选择方法往往只保留一组最佳波段组合，而其余未选中的波段则被抛弃。这对于最后的分类任务意味着较多的鉴别信息损失，因而波段选择后的分类正确率还有较大提升空间。

本文从提高图像分类正确率角度出发，提出一种新的波段选择方法，将多分类器组合的思想运用于高光谱波段选择中。本文重新定义的高光谱波段选择问题为:给定待选择的最大波段数目N，如何选择k组波段子集，使组合后的分类正确率更高，每组波段子集的波段数为n，这k组波段子集中包含的不同波段总数不超过N。以往的波段选择研究都是从选择一组最优波段子集角度出发，最大化该组被选中波段的分类正确率。本文则基于初步选择出的多个不同较优波段子集，构成多个特征子空间进行多分类器组合，从分类器互补性及多样性角度重新选择出满足最大波段数约束的最佳波段组合，进一步提高分类正确率。

具体地，首先多次采用基于遗传算法的波段选择算法获得若干组相对较优的波段子集，再基于这些波段子集分别训练支持向量机得到若干个基分类器，然后通过多分类器组合方法对这些基分类器进行组合。在组合之前，根据最大波段数目约束条件进行了多分类器选择，从而实现最后的波段选择。具体采用基于差异性度量的带有波段数目约束的分类器选择算法选出部分较优分类器组合，得到一组互补性及错误多样性较好的分类器。最后采用基于局部分类精度的动态分类器选择组合方法，根据每个分类器对测试样本邻域中若干训练样本的分类正确率从多个分类器中选出最优的一个分类器作为决策判断分类器，获得最终分类结果。

本文提出的波段选择方法有两轮搜索选择过程，第1轮采用常规搜索方法获得多个较优波段子集，在第2轮则采用多分类器组合思想，选择若干具有较强互补性与多样性的波段子集，使更多的具有鉴别力的波段能在第2轮组合选择中获得被选中的机会。较之传统一次(最优)选择方法，本文方法在有效地规避了高光谱数据高维特征问题的同时，保留了更多的鉴别信息，明显提高了分类精度。

1 多分类器组合方法

波段选择优劣的评判标准除了选择的波段数外，往往是通过最终的分类正确率来衡量，针对高光谱数据波段间相关性高的特点，本文将多分类器组合的思想引入高光谱波段选择中。多分类器组合是根据各个分类器的整体性能将每个分类器的输出按某种方式“组合”到一起，并达到“共识”[13]。同时，多分类器系统的性能很大程度上取决于成员分类器的差异性，为了选出具有较强错误差异性的分类器组合，本文研究了聚类选择法以及基于局部分类精度的动态分类器选择两种组合方法。另外，多分类器组合方法可以根据单个分类器输出类型分为抽象级、排序级和度量级3类，本文选择基于抽象级的几种分类器组合方法，如多数投票法、行为知识空间法对基于不同特征子空间训练的分类器进行组合。

1.1 多数投票法(majority voting)

投票法是最常用的抽象级分类器组合方法，其遵循的原则是“少数服从多数”。多数投票规则[13]将最多数分类器一致分类的类别作为待分类样本的类别。当出现多个类别获得的投票数目相同时，一般随机选择其中一个类别作为最终的结果。此外，考虑到不同分类器的分类正确率，也可以对各个结果按照分类器不同表现设置不同的权重，进行加权投票。

1.2 行为知识空间法(behavior－knowledge space，BKS)

很多分类器组合方法都需要假设分类器之间相互独立。在无法满足该假设的情况下，可以考虑从知识空间获得信息，它能同步记录所有分类器对每个训练样本的决策。由于知识空间记录了所有分类器的行为，所以也被称为“行为知识空间”，简称BKS[14]。使用该方法时，训练集中的样本被划分成不同的模式，这些模式是根据所有分量分类器分类结果的不同组合来定义的。当一个未知样本需要进行分类时，所有分量分类器对分类结果的组合都是已知的，由此确定对应的模式。然后根据该模式中的样本实际类别，把未知样本归入出现次数最多的类别。

1.3 聚类 － 选择法(clustering－selection)

聚类－选择算法训练过程如下:

1)利用训练数据集Z训练L个基分类器C1，C2，…，CL，初始化聚类数 K;

2)通过K－均值方法将Z聚成K类(不考虑样本集的真实类别)，通过计算每个簇中的样本均值得到聚类中心 V1，V2，…，VK;

对于该算法，如何选择一个合适的K值是很重要的问题，本文实验对参数K做了大范围的搜索，详见实验分析。

1.4 局部精度估计的动态分类器选择(DCS－LA)

DCS－LA方法[16]的主要特点是对于待分类样本X*，从已有的基分类器C1，C2，…，CL中动态挑选合适的一个或多个对其进行分类，或者样本所在邻域内最优的分类器来对其进行分类，它是一种特殊的分类器集成方法，其主要步骤为:

1)如果所有的分类器Cj返回X*相同的类别ω，则该测试样本被赋予类别ω，算法结束，否则转2);

2)计算每个基分类器的局部分类精度LAj，kX(*)，j=1，2，…，N，k为X*邻域内训练样本数;

3)确定局部分类精度最高的基分类器Cj，使，并将Cj的输出作为X*的类别，算法结束。

从以上步骤可以看出DCS－LA的分类正确率主要取决于局部分类精度估计，本文采用基于先验知识的局部精度。该方法将局部分类精度的局部邻域RkX(*)内被正确分类的训练样本比例。假设Rk(X*)内有k个训练样本，其中有kT个样本被Cj正确分类，则分类器Cj对X*的局部分类精度为

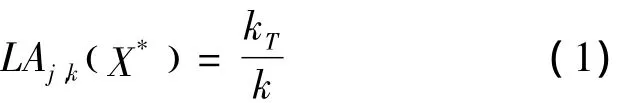
由于在选择分类器时没有考虑分类器Cj对测试样本X*的分类结果，所以一般称之为先验局部精度估计。

2 多分类器组合的高光谱波段选择方法

传统的波段选择需要在整个原始波段空间进行搜索，本文针对高光谱图像波段多且相关性高等特点，提出将多分类器组合的思想运用于高光谱波段选择中，通过遗传算法搜索得到K组较优波段组合，使用这K组波段组合分别训练K个基分类器，然后从这K个分类器中选出部分差异性较大的分类器进行组合，实现波段选择的目标。最后分类测试时采用基于局部分类精度的动态分类器选择方法(DCS_LA)得到最后的分类结果。

上述过程中，存在两次多分类器组合过程。在第1次分类器选择时，采用基于错误多样性度量的带波段数目约束的多分类器选择方法。在多分类器组合研究中，研究人员[17－18]已经发现从基分类器中去除一些作用不大和性能不好的分类器，剩下的少量分类器能够获得更好的预测效果。因此本文在高光谱波段选择多分类器组合过程中，也进行了分类器选择。由于本文的目的是通过多分类器组合实现波段选择，因此希望选择的分类器数目较少，这样最终的波段总数才能更加符合用户要求。

以往的多分类器选择研究中，主要考虑分类器之间的互补性和多样性，特别是错误多样性(error diversity，亦称为差异性)。Aksela 和 Laaksonen[19]分析比较了各种错误多样性指标，发现同误多样性指标(same－fault measure)具有不俗的表现。该指标考虑2个分类器如果犯相同错误的概率较小，则组合后获得正确分类结果的可能性更大。由于高光谱波段选择多分类器组合过程中不但需要获得更高的分类正确率，而且希望组合后参与分类的波段总数尽可能少，因此在最小化相同错误概率的同时，还要最大化同时正确的概率。因此，提出如下错误多样性指标:

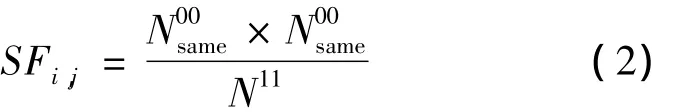
在选择分类器过程中，分别考察候选分类器与各个已经选择分类器之间的错误多样性，选择与已经选择分类器错误多样性指标之和最小的分类器。算法1 带波段数目约束的多分类器选择算法输入:给定选择波段总数上限total，K组波段数目为 n 的分类器集合

输出:分类器集合S。

1)初始化S为空集;

2)根据每个分类器在训练集上的分类精度选取分类精度最高的第一个分类器，记为Ci，将Ci加入S，S=S∪ { Ci}，同时从U中减去 Ci，U=U{ Ci};

3)根据式(2)计算U中每个分类器Cp和S中已经选取的各个分类器Cq的多样性SFp，q;

4)对于 U中每个分类器 Cp，P=1，2，… ，为集合U中分类器数目，计算其与S中已经选取的各个分类器的错误多样性之和:

式中:SFp，q为分类器Cp、Cq之间的错误多样性度量值，Cq为S中已经被选取的各个分类器，表示已选分类器集合中分类器数目;

5)挑选Scorep最小的分类器，记为Cj，计算Cj和S中各分类器对应波段的并集Sall，如果Sall的波段总数|Sall|＜ =total，则将Cj加入S，S=S∪{Cj}，从U中减去Cj，U=U{ Cj} ，转(2)，否则转6)

6)算法结束，返回S。

在对测试样本进行分类时，由于前面选择得到了若干分类器，可以采用多分类器组合的方法确定其最终类别。通过比较分析各种常见分类器组合方法(具体见实验部分)，最终采用基于局部分类精度的动态分类器选择(DCS－LA)方法进行组合。根据文献[16]中的基于局部分类精度估计的方法，对于每个测试样本，利用1.4节中基于先验知识的局部精度估计方法计算S中各分类器在该样本邻域的局部精度(local accuracy，LA)，选出LA最高的分类器作为其最终的决策分类器。分类过程如下。

算法2 基于局部分类精度的动态分类器选择的分类算法

输出:测试样本x的类标签y

1)针对测试样本x，基于不同特征空间(对应组合分类器S中不同的成员分类器)寻找它的k个最近邻训练样本点，通过每一个分类器对k个最近邻样本点进行分类;

2)选择出S中局部分类精度最高的分类器Cj，作为该样本的最终分类器;

3)利用Cj对x进行分类，得到的类别标签y即为最终分类结果。

3 实验结果与分析

本文采用的高光谱图像测试数据集为Indian Pine数据集[1]。原始Indian Pine数据集包含220个连续的波段，其中18个波段由于受大气影响而被丢弃，因此剩下202个有效波段。该图像数据包含玉米区、树林、黄豆以及牧场等9种类别的样本，测试样本与训练样本不是随机分配，而是对每类分别定义空间不相交的测试区与训练区，以尽可能减少它们的相关性，最终实验数据包括训练样本5 012个，测试样本3 728 个[3]。

3.1 对比实验1

为了比较出对高光谱数据波段选择具有最优效果的多分类器组合方法，本文实现了四组多分类器组合方法，分别是多数投票法、行为知识空间法、K均值聚类选择法以及基于局部分类精度估计的动态分类器选择法。在进行多分类器组合之前，首先通过文献[8]中方法，即利用条件互信息将202个有效波段分成12组，再使用GA－SVM的方法搜索出相对较优的波段子集，多次利用该方法获取10组波段子集后，将这些相对较优的波段子集训练成10个基分类器(10组分类器含有波段总数为47，每个子集12个波段)，然后使用上述4种多分类器组合方法对这10个基分类器进行组合。

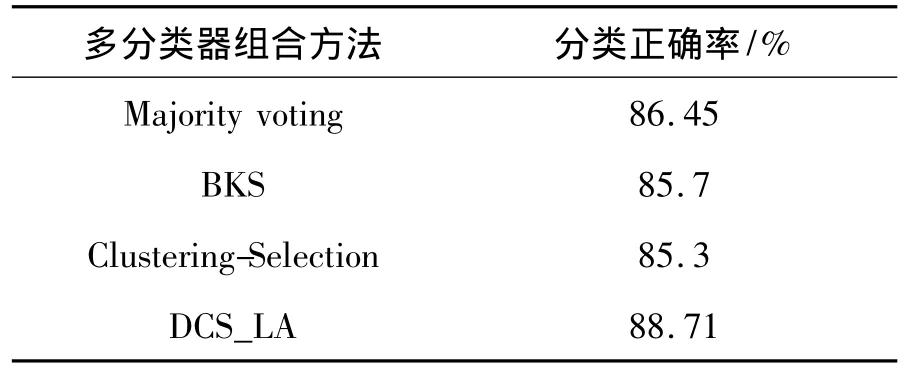
表1 4种不同分类器组合方法的分类精度Table 1 The classification accuracy based on classifiers combination methods of four different

表1给出了4种多分类器组合方法的分类精度比较。4组实验都选取所有10个基分类器，共47个波段。从表1中可以看出，行为知识空间法，即BKS方法比多数投票法效果稍差，这主要是因为对于高光谱数据具有“同谱异物”的特点，分类时测试样本输出模式与训练样本的输出模式匹配时，相同模式有很多是同样被错误分类的，即相同错误的分类器的差异性不够明显，直接导致了分类结果趋向错误分类的那一部分。本文实验中采用的K－均值聚类对参数K做了(10，500)范围的搜索，最后当K为200时，取得85.3%最佳的效果。聚类选择方法作为无监督学习方法，没有考虑训练样本的类别分布，所以在分类中很难占有优势。显然，DCS－LA的分类精度最高，说明通过该算法对多分类器进行组合比较有效。在分类器选择过程中，还可以调整选择的分类器数目，即对应选择的波段数目，详见对比实验2。

3.2 对比实验2

为了进一步验证多分类器组合算法对波段选择的有效性，本文进行了5组实验，分别选择不同波段总数限制的多个分类器，然后进行基于DCS－LA组合方法的分类测试，表2给出了这几种情况的详细分类精度。从表2中可以看出，通过确定分类器组合总体多样性，即对应波段总数上限total，选择的分类器组合数目也不相同，选取的波段数目也各不相同。当波段总数为50时，即对全部10个基分类器进行组合时，分类结果最好，正确率达到了88.71%。而选择波段不超过30个时，只选择了4个分类器，此时分类正确率为88.39%，明显高于利用所有202个波段进行分类的精度83.2%;而与10个分类器全部参与组合的正确率也很接近，表明在本文研究的高光谱波段选择中，动态选择参与组合的分类器确实比较有效，既减少了参与组合的分类器，也达到了波段选择的目的。

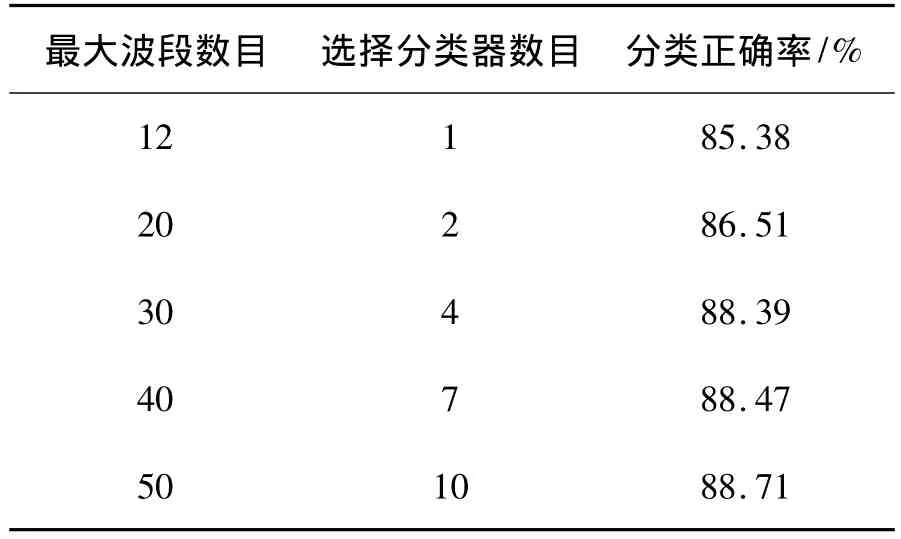
表2 基于不同波段数目约束的动态分类器选择的分类精度Table 2 The classification accuracy of dynamic classifier selection based on different numbers of bands

3.3 对比实验3

为了证明本文算法较之传统搜索算法的优点，使用另外2种常用的全局波段空间搜索的高光谱波段选择方法与本文算法进行比较这两种方法分别是遗传算法的波段选择方法和文献[12]中的自适应分支定界法搜索的波段选择方法。在此，采用两种方法同样分别搜索12、20、30、40、50 个波段进行最后的分类，由于遗传算法的随机性，对每一组波段分别搜索3次，取3次分类结果进行平均得到平均分类精度，如表3。

表3 遗传算法、分支定界法以及本文算法的平均分类精度Table 3 The average classification accuracy of GA，BB and the proposed algorithm

从表3可以看出，当波段数目分别为12、20、30、40、50时，本文算法在分类正确率上具有明显的优势，其中，遗传算法在波段数目为40时达到最高分类正确率84.34%，自适应分支定界法在波段数目为30时达到最高分类正确率85.20%，而本文算法使用局部分类精度的动态分类器选择，在对应波段数目为30时，达到了88.39%的分类正确率，明显高于其他2种直接搜索一组最优波段子集的方法，因此本文方法具有较强的竞争力。

3.4 讨论

多分类器组合在遥感图像分类，特别是高光谱图像分类中得到了广泛关注[20]。Skurichina and Duin[21]研究了基于多次特征选择的多分类器组合方法，他们采用多次序贯选择特征子集的方法获得多个基分类器，每次从前一次选择余下的特征中选择次优的特征子集，最后将所有基分类器进行组合集成。该方法与本文方法的不同有2点:1)所有特征参与了最后的分类决策，每个特征都被分配到一个基分类器;2)所有分类器都参与了决策融合。文献[22]研究了多支持向量机集成的高光谱图像分类方法。该方法通过波段间相关性将波段分组，然后构建多个支持向量机分类器;最后的分类结果是以多个支持向量机的输出再输入另一个支持向量机后得到的输出。该方法也是所有波段都参与了分类决策。Du等[23]研究了基于证据融合的多分类器组合方法及其在高光谱图像分类中的应用。该文采用的基分类器有马氏距离分类器、多层前向神经网络、径向基神经网络、支持向量机以及决策树。同样，该文关注的是多分类器集成在高光谱图像分类中的适应性，并未考虑波段选择问题。

4 结束语

本文提出了一种基于多分类器组合的高光谱波段选择方法，通过多次采用遗传算法搜索出相对较优的若干组波段组合，然后分别将这些波段组合训练成若干基分类器，再使用基于错误多样性度量的分类器选择算法选择出其中符合最大波段数约束的部分分类器，达到波段选择的目的。在此基础上，采用DCS－LA动态分类器选择方法，选取具有最高LA的分类器的输出作为最后分类结果，通过实验验证了多分类器组合的波段选择方法的有效性。

多分类器组合研究是当前模式识别领域的研究热点之一，本文提出了基于多分类器组合方法来应对高光谱数据高维度且波段相关性高的问题。多分类器组合的作用主要在于降低高维波段搜索问题及提升分类性能，而真正有效地提高分类准确率还依赖于成员分类器的整体差异性的增大。差异性的研究是多分类器组合系统研究的关键问题之一，目前还没有被广泛接受的理论与方法。定义新的差异性度量并以此来构造和训练多分类器组合系统，更好地提高多分类器组合的有效性是下一步需要研究的方向。

[1]LANDGREBE D A.Signal theory methods in multispectral remote sensing[M].John Wiley ＆ Sons，2005:5－12.

[2]SERPICO S B，BRUZZONE L.A new search algorithm for feature selection in hyperspectral remote sensing images[J].IEEE Transactions on Geoscience and Remote Sensing，2001，39(7):1360－1367.

[3]BAZI Y，MELGANI F.Toward an optimal SVM classification system for hyperspectral remote sensing images[J].IEEE Transactions on Geoscience and Remote Sensing，2006，44(11):3374－3385.

[4]SOTOCA J M，PLA F.Hyperspectral data selection from mutual information between image bands[M].Berlin:Springer，2006:853－861.

[5]GUO B，DAMPER R I，GUNN S R，et al.A fast separability－based feature－selection method for high－dimensional remotely sensed image classification[J].Pattern Recognition，2008，41(5):1653－1662.

[6]戴宏亮，戴道清.基于ETAFSVM的高光谱遥感图像自动波段选择和分类[J].计算机科学，2009，36(4):268－272.DAI Hongliang，DAI Daoqing.Automatic band selection and classification of hyperspectral remote sensing images based on ETAFSVM[J].Computer Science，2009，36(4):268－272.

[7]吴昊，李士进，林林，等.多策略结合的高光谱图像波段选择新方法[J].计算机科学与探索，2010，4(5):464－472.WU Hao，LI Shijin，LIN Lin，et al.Multiple－strategy combination based approach to band selection for hyper－spectral image classification[J].Journal of Frontiers of Computer Science and Technology，2010，4(5):464－472.

[8]YANG He，DU Qian，SU Hongjun，et al.An efficient method for supervised hyperspectral band selection[J].IEEE Geosci Remote Sensing Lett，2011，8(1):138－142.

[9]葛亮，王斌，张立明.基于波段聚类的高光谱图像波段选择[J].计算机辅助设计与图形学学报，2012，24(11):1447－1454.GE Liang，WANG Bing，ZHANG Liming.Band selection based on band clustering for hyperspectral imagery[J].Journal of Computer－Aided Design ＆ Computer Graphics，2012，24(11):1447－1454.

[10]王立国，魏芳洁.结合遗传算法和蚁群算法的高光谱图像波段选择[J].中国图象图形学报，2013，18(2):235－242.WANG Liguo，WEI Fangjie.Band selection for hyperspectral imagery based on combination of genetic algorithm and ant colony algorithm[J].Journal of Image and Graphics，2013，18(2):235－242.

[11]LI Shijin，ZHU Yuelong，WAN Dingsheng，et al.Spectral similarity－preserving hyperspectral band selection[J].Remote Sensing Letters，2013，4(10):969－978.

[12]SERPICO S B，MOSER G.Extraction of spectral channels from hyperspectral images for classification purposes[J].IEEE Transactions on Geoscience and Remote Sensing，2007，45(2):484－495.

[13]ZHOU Z H.Ensemble Methods:Foundations and algorithms[M].Boca Raton:CRC Press，2012.

[14]KUNCHEVA L I.Switching between selection and fusion in combining classifiers:an experiment[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B:Cybernetics，2002，32(2):146－156.

[15]KUNCHEVA L I，WHITAKER C J.Measures of diversity in classifier ensembles and their relationship with the ensemble accuracy[J].Machine Learning，2003，51(2):181－207.

[16]WOODS K，KEGELMEYER JR W P，BOWYER K.Combination of multiple classifiers using local accuracy estimates[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，1997，19(4):405－410.

[17]ZHOU Z H，WU J X，TANG W.Ensembling neural networks:many could be better than all[J].Artificial Intelligence，2002，137(1/2):239－263.

[18]张春霞，张讲社.选择性集成学习算法综述[J].计算机学报，2011，34(8):1399－1410.ZHANG Chunxia，ZHANG Jiangshe.A survey of selective ensemble learning algorithms[J].Chinese Journal of Computers，2011，34(8):1399－1410.

[19]AKSELA M，LAAKSONEN J.Using diversity of errors for selecting members of a committee classifier[J].Pattern Recognition，2006，39(4):608－623.

[20]BENEDIKTSSON J A，CHANUSSOT J，FAUVEL M.Multiple classifier systems in remote sensing:from basics to recent developments[C]//Proceedings of the 7th International Conference on Multiple Classifier Systems.:Berlin:Springer－Verlag，2007:501－512.

[21]MARINA S，ROBERT P W.Combining feature subsets in feature selection[C]//Proceedings of the 5th International Conference on Multiple Classifier Systems.Berlin，2005:165－175.

[22]XAVIER C，BJöRN W，JON A B，et al.Ensemble strategies for classifying hyperspectral remote sensing data[C]//Proceedings of the 9th International Conference on Multiple Classifier Systems，Berlin:Springer－Verlag，2009:62－71.

[23]DU Peijun，ZHANG Wei，SUN Hao.Multiple classifier combination for hyperspectral remote sensing image classification[C]//Proceedings of the 9th International Conference on Multiple Classifier Systems，Berlin，2009:52－61.