三角形横向荷载作用下的简支梁弯曲分析
付明春,李殿平
(大连海洋大学,辽宁 大连116300)
在实际工程中,某些梁和立柱杆件同时受纵、横两个方向载荷作用,其变形为压弯组合变形.对弯曲刚度很大的杆件,由于弯曲变形微小,轴力引起弯曲应力和变形可以忽略不计,可按线弹性叠加原理确定梁的最大挠度和最大弯矩[1]. 工程实际中,若横向荷载引起的弯曲挠度使截面形心偏离原位置的距离较大,轴力引起的弯矩就必须予以考虑.目前对横向荷载为均布荷载时的情况已有讨论[2],而对横向三角形荷载作用下的最大挠度和最大弯矩计算还没有深入研究.在水利、建筑工程中,有些结构如挡土立柱、放水闸门的胸墙等,其横向荷载多按三角形规律分布,故研究三角形分布的横向荷载引起的纵横弯曲具有现实意义.笔者就此情况展开研究,给出梁或立柱杆件在三角形横向荷载作用下产生纵横弯曲变形时的最大挠度和最大弯矩数值和位置的确定方法,并以水闸结构中的胸墙为例,阐明所推导公式的具体应用.
1 挠曲线微分方程的建立和通解确定
图1为同时受横向荷载和轴向荷载作用的简支梁,其中横向荷载集度为q(线性分布),轴向力为F,x 截面上的弯矩为
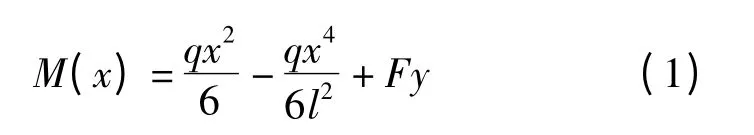
式中:M 为弯矩;l 为杆件长度;F 为作用在杆件两端的轴向力;y 为杆件的挠度;x 为任意位置处点的横坐标.
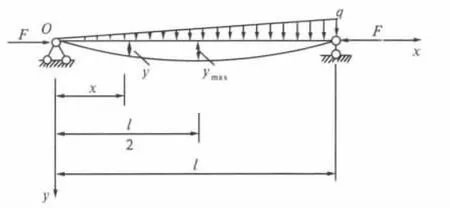
图1 简支梁同时受轴向力和三角形横向荷载作用的受力图
于是,可得挠曲线微分方程为
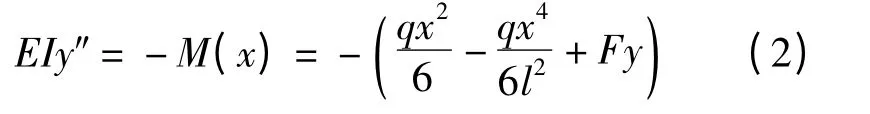
式中:E 为材料的杨氏弹性模量;I 为杆件横截面对中性轴的惯性矩;x 为任意位置处点的横坐标.
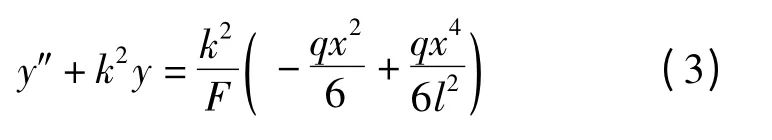
这是一个二阶线性非齐次微分方程.其解为齐次方程的通解加上非齐次方程的一个特解. 齐次方程的通解为Y,相应的齐次方程为
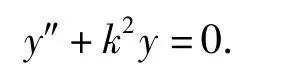
特征方程r2+k2=0 的通解是r = ±ik.故齐次方程的通解为
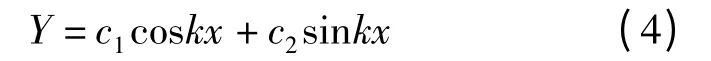
设非齐次方程的一个特解是y*,对于形如y″+py' +q=pm(x)eλx型的常系数方程具有标准的解法.由于这里,λ=0 不是齐次方程的根,于是可设
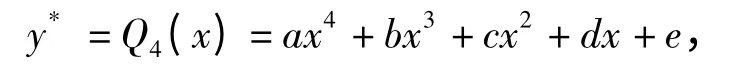
将此一元4 次多项式代入原方程,使用待定系数法有:
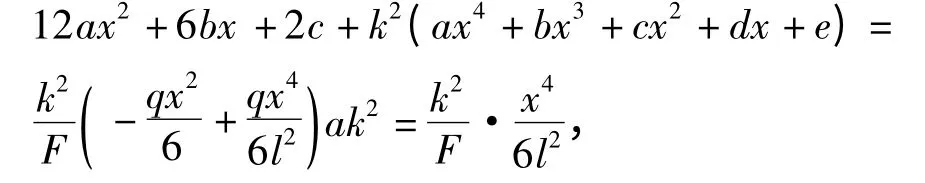
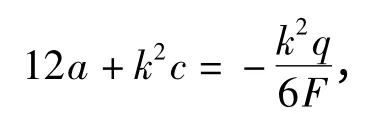
可求出c 值,即
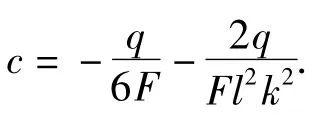
由6b+k2d=0,得d=0.由k2e+2c=0,求得
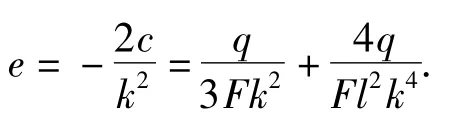
故y*=ax4+cx2+e,其中a,c,e 如上式所示,则
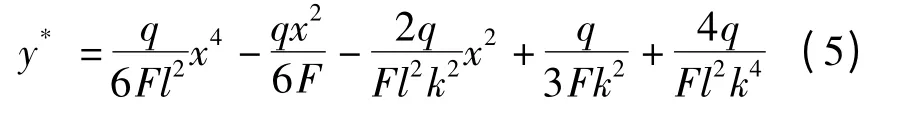
方程的通解为:y=Y+y*,则
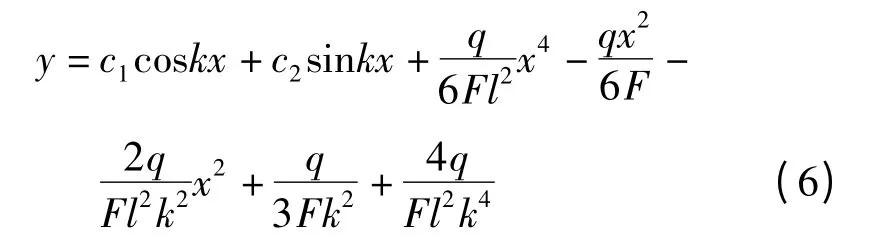
当x=0,y=0,x=l,y=0 时,分别求出c1,c2.
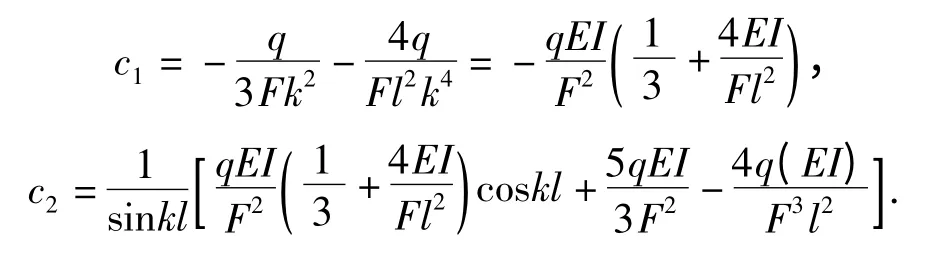
将c1,c2代入通解方程(6),获得最终表达式:
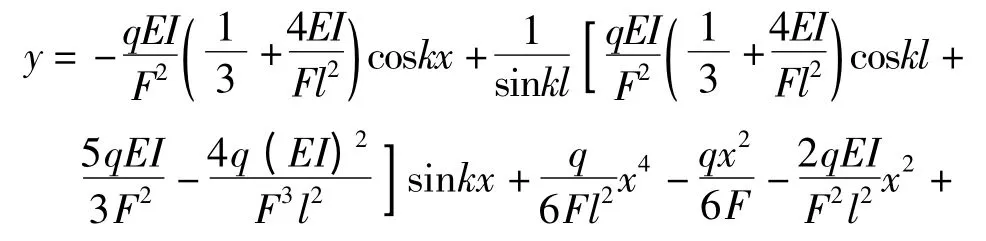

2 跨中挠度与弯矩分析
因荷载为非均布荷载,故挠度最大值不在跨中,但实验表明其值与跨中(即x =l/2)处的挠度接近[3].如果取跨中(即x =l/2)值代替,即将x =l/2代入式(7)中可得:

考虑到跨中挠度对跨中弯矩的影响,可以根据跨中(x=l/2)处的挠度求出跨中弯矩,即
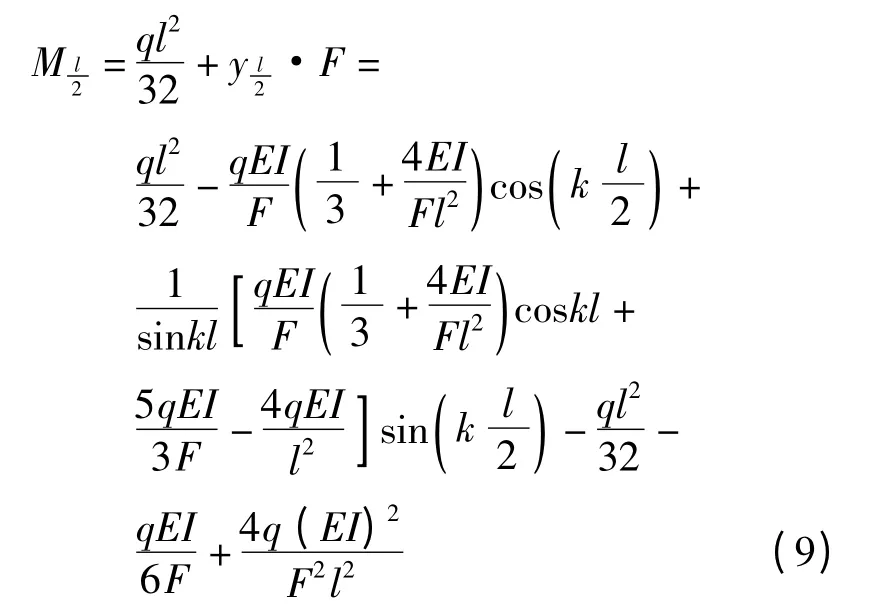
3 最大弯矩与最大挠度分析
由式(1)给出的弯矩函数可知,若不考虑轴向力F 的影响,梁的弯矩函数应该为

对该式求导并令导数为0,得
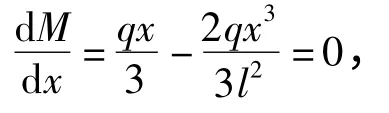
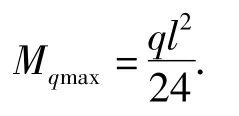
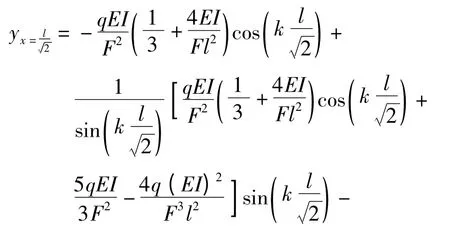
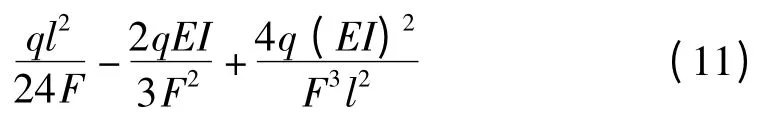
考虑轴向力F 产生的弯矩影响[4-5],当时,弯矩
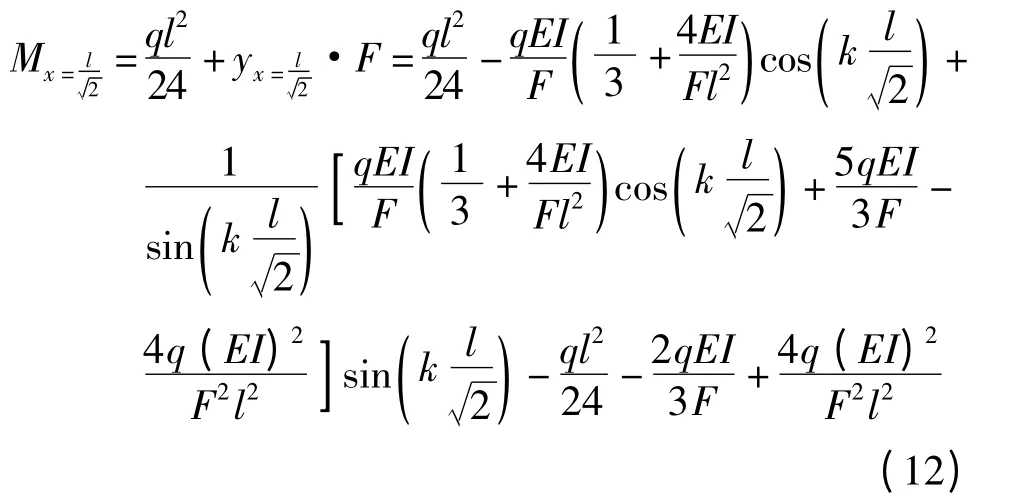
在此,需要说明的是,式(11)和式(12)仅由横向力弯矩函数推导而得.
4 实例分析
工程实际当中,带有胸墙的水闸可以简化为如图2和图3所示的力学结构简图[6],与图1相似.现模拟实际情况,通过文中导出的公式对胸墙的挠度和弯矩进行分析和计算.
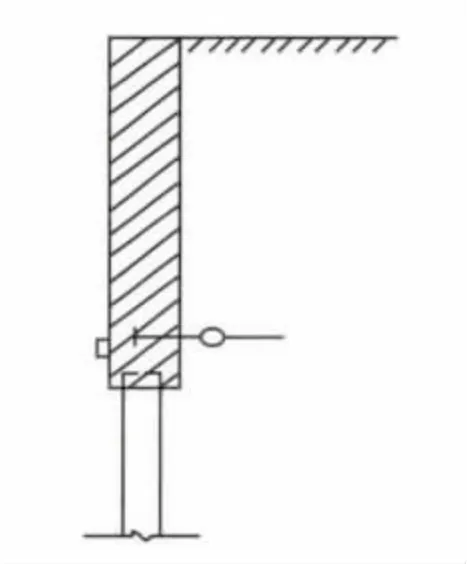
图2 胸墙力学结构简图
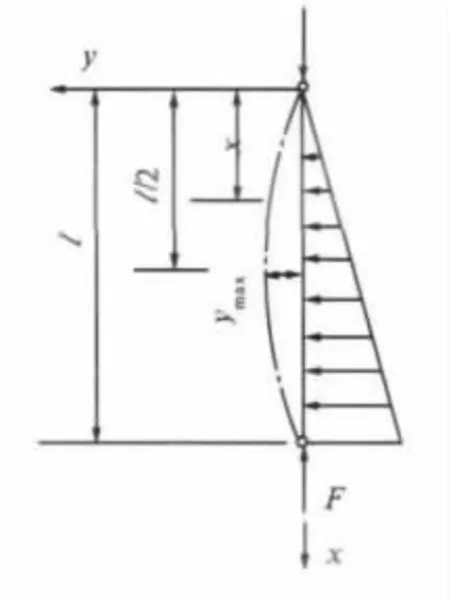
图3 胸墙结构的受力图
某水闸结构中的胸墙采用10 号工字钢,跨度l=2 m,I =245 cm4,E =200 GPa,水荷载最大集度q=20 kN/m.在不同轴向力F 作用下,根据式(8),(9),(11),(12)计算x=l/2(跨中)时截面上的挠度和弯矩,结果见表1.
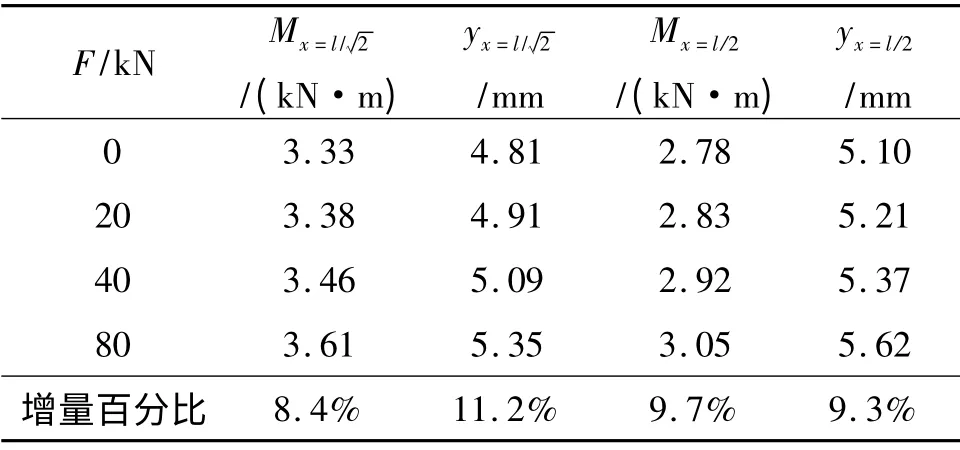
表1 挠度和弯矩计算结果
以表1中数据8.4%为例,其计算表达式为
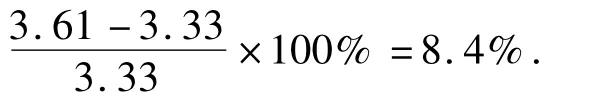
由表1可知:当轴向力较小时,对弯矩值影响不大;当轴向力较大、在横截面上产生的压应力接近材料的比例极限时,构件横截面上的最大弯矩和最大挠度与不考虑轴向力、只有横向荷载作用时产生的最大弯矩、最大挠度相比约增加了10%左右. 实例中给出的10 号工字钢的比例极限为200 MPa[7],轴向荷载为80 kN 时,截面的应力为
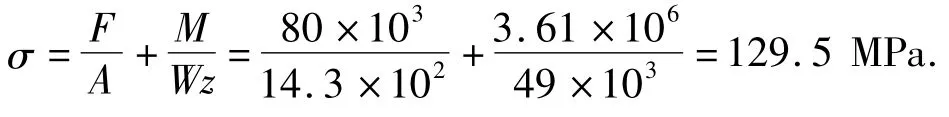
式中:A 为10 号工字钢的横截面面积,mm2;M 为杆件的最大弯矩,N·mm;Wz 为10 号工字钢的抗弯截面系数,mm3.
该结果没有超过材料的比例极限200 MPa. 可见,考虑轴向荷载作用对最大弯矩和最大挠度的影响时,最大挠度的位置接近于x =l/2 处,最大弯矩的位置接近于处. 综合分析,最大挠度和最大弯矩一定在x=l/2 和之间的某截面.
工程中若要进一步确定最大弯矩和最大挠度的相对精确位置,可采用试算法进行计算[8]. 在此,以轴向荷载为80 kN 为例确定最大挠度和最大弯矩的位置.将不同的x 坐标(坐标差取0.05l)分别代入式(1)和式(7)进行计算.结果见表2.
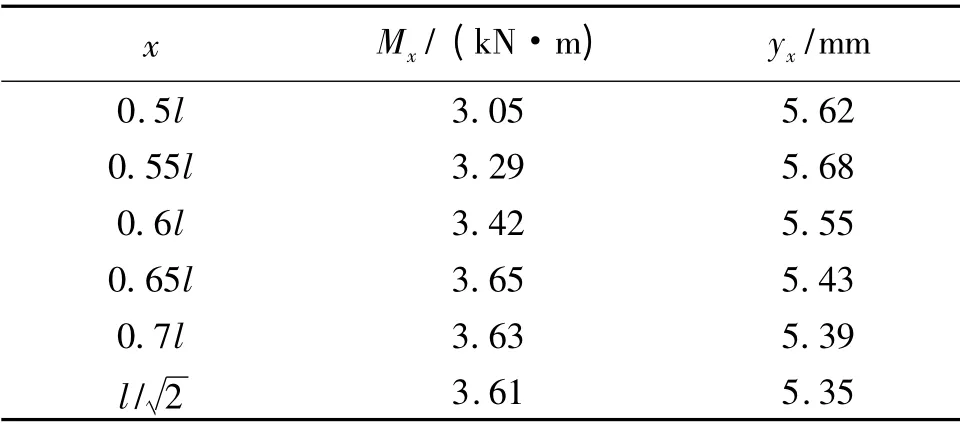
表2 最大弯矩和最大挠度试算结果
从表2可以看出,最大弯矩在0.65l 处,最大挠度出现在0.55l 处.
5 结 语
1)应用文中给出的方法可对水闸结构中的胸墙、煤矿顶板的支护杆件等进行稳定性分析与计算、分析稳定性事故原因等,可以避免大量繁琐的计算,在工程实际中具有重要的意义.
2)以上的分析仅限于对杆件在xy 平面内的纵横弯曲变形的研究,如果杆件在xz 平面内弯曲刚度较小,还需进行稳定性分析.
[1]李文飞,李玄烨,黄根炉. 基于纵横弯曲梁理论的水平井管柱摩阻扭矩分析方法[J].科学技术与工程,2013,13(13):3577-3583.
[2]孙训芳,方孝淑,关来泰. 材料力学(Ⅰ)[M]. 北京:高等教育出版社,2009.
[3]刘文顺,苏军,王洪波. 钢结构[M]. 哈尔滨:黑龙江教育出版社,2008.
[4]李殿平,李整建.工形变截面钢折拱梁的受力分析[J].焦作大学学报,2010(4):98-99.
[5]齐红军.工程力学[M]. 哈尔滨:哈尔滨工业大学出版社,2012.
[6]杨晓伟,赵海峰,韩志虎. 拉西瓦水电站泄水坝段进水口胸墙模板设计制作及施工[J]. 水力发电,2009,35(11):30-31.
[7]北京钢铁设计研究总院. GB 50017—2003 钢结构设计规范[S].北京:中国计划出版社,2003.
[8]李成,许晓芳.压杆纵横弯曲的高阶应变理论解[J].新乡学院学报:自然科学版,2010,27(1):16-18.

