基于电气外特性的光伏发电系统模型等效方法

刘兴杰 郭 栋 王凯龙

（华北电力大学新能源电力系统国家重点实验室 保定 071003）

1 引言

光伏发电以其清洁、可再生等优势，在世界范围内得到了高度重视。在过去的20 年里，光伏发电以每年20%～25%的幅度递增[1,2]。随着越来越多的分布式光伏发电系统接入电网，其对电网的影响日益显现，需对此进行相关研究，而光伏发电并网系统模型是所有研究分析的基础。根据光伏发电并网系统模型的构成，国内外研究者在光伏阵列、MPPT（最大功率点跟踪）和逆变器的控制策略等方面展开了大量研究，提出了许多模型和方法[3-14]、其中工程用数学模型[3,4]，扰动观测法[7,8]及基于SPWM的电压电流双环控制策略[12]由于具有响应速度快或算法实用等各自的优点而被普遍采用。

然而，采用现有光伏发电系统模型进行仿真计算时，需先根据输入的光照强度和温度进行运算，解出光伏阵列的输出电流，并将其转化为电气信号输入到Boost 电路；然后在MPPT 的作用下，通过调节电力电子器件的占空比从而使光伏阵列工作在最大功率，并输送到逆变系统；最后再由逆变器的控制策略，通过将并网点的电压电流经过锁相、坐标变换、PI 积分和坐标反变换等计算环节，得出调制波并在PWM 的作用下形成逆变器的触发脉冲，从而完成整个并网过程的一次计算。由此可见，随着接入配电网的光伏电源越来越多，若对每个光伏电源及其内部连接都采用类似的详细模型，将会使其对应的模型变得十分复杂，可能带来诸如模型有效性、数据修正、内存占用大和仿真时间长等问题。因此，需要探寻一种较为实用的光伏发电系统等效模型以提高计算效率，而相关研究却较少。

对于电网来说，更为关注的是所接入的光伏发电系统的输出电压、电流以及有功无功等电气量。基于此，本文从光伏发电系统的外特性角度对其等效模型进行了深入研究。首先通过系统地分析光伏电源输出特性建立光伏电源稳态等效模型；然后通过推导故障电流的求解方程组，在对系统传递函数降阶的基础上，建立光伏电源暂态等效模型；最后将二者结合获得光伏电源的最终等效模型。借助Matlab/Simulink 仿真平台，对比验证了等效模型和详细模型下的电气输出特性和计算效率。

2 光伏发电系统详细模型

并网光伏发电系统由光伏阵列、MPPT、逆变器、滤波电路及隔离变压器组成。

2.1 光伏阵列数学模型

光伏阵列由大量光伏组件组成，其输出电流为

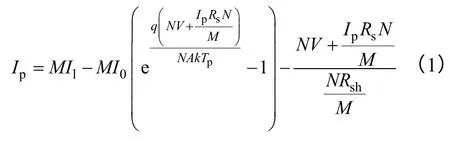
式中，V、Ip为光伏阵列的输出电压和电流；N为光伏组件串的串联数；M为光伏组件串的并联数；Il为单位光伏组件所产生的光电流；I0为二极管的反向饱和电流；A为光伏组件的理想因子；Rs、Rsh为单位光伏组件的串联和并联阻抗；k为玻耳兹曼常数；q为电荷常数；Tp为电池表面温度。

2.2 光伏阵列的最大功率点跟踪

光伏阵列最大功率点跟踪的原理是通过检测光伏阵列在不同工作点下的输出功率，经过比较寻优，找到光伏阵列在确定日照和温度条件下输出最大功率时对应的工作电压，从而保证其在任何自然条件下不断获得最大功率，进而提高效率，充分运用太阳能。常用的MPPT 方法有扰动观测法、增量电导法和短路电流和开路电压法等[7-10]。本文的详细模型中采用了扰动观测法，该方法由于具有实现简单、运算量小等优点，在工程中应用广泛。

2.3 逆变器模型

根据PWM 工作原理，可以通过改变其调制波的相位与调制度来调节逆变器交流侧输出的基波电压相角和幅值，从而控制输送的有功和无功功率。比如电压电流双环控制，以电压、电流输入信号和为换流器控制输入量，经过PI 调节、限幅和PWM调制，得到换流器开关器件的触发脉冲。这样既可以控制换流器的电压又可以快速跟踪从最大功率跟踪环节计算得来的最大功率。锁相环节PLL 跟踪电网电压的相位，为电压频率控制和触发脉冲生成提供基准相位[15]。双闭环控制策略由于保证了对输出电流的要求，并且具有控制物理意义明确、易于软件实现和动态响应快等优点，故应用普遍。

此外，当电网发生不对称故障时，为了降低光伏发电系统输出的谐波，改善输出特性，许多文献都提出了各种改进策略[16-18]，其中，正序分量控制是最常用的策略。因此，本文详细模型的逆变器采用带正序分量控制的双闭环控制策略。

3 光伏发电系统的外特性分析

光伏发电系统的电气外特性是指光伏电源的输出电压、电流以及有功无功等电气量，包括稳态外特性和暂态外特性。

3.1 稳态外特性

式（1）中的几个参数（包括Iph、I0、Rsh和Rs等）与电池温度和太阳光强有关，确定十分困难，且太阳电池生产厂商也不提供这几个参数，因此，式（1）不适用于光伏发电系统工程设计。工程模型通常要求仅采用厂商提供的技术参数（Isc、Voc、Im和Vm）就能在一定的工程精度下描绘出PV 的I-V特性，以便于计算机仿真分析。经过近似简化后，对应于最大功率点的电压和电流可表示为[19]

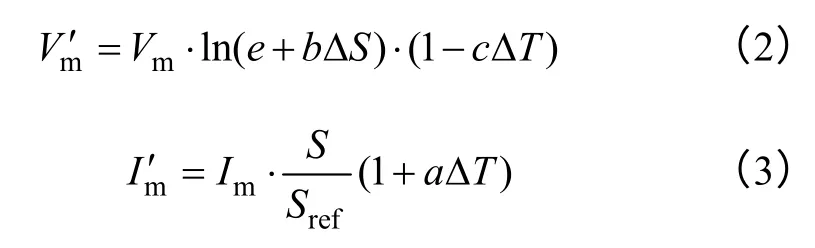
式中，ΔS=S-Sref，ΔT=T-Tref，Sref和Tref分别为参考辐射强度（1 000W/m2）和参考电池温度（25℃）；补偿系数a、b、c为常数，根据大量实验数据拟合，其典型值推荐为：a=0.002 5(℃)-1；b=0.000 5(W/m2)-1；c=0.002 88(℃)-1。

显然，由于光伏电源的输出特性与光照强度和温度有关，并依靠MPPT 能保证最大功率，所以最大输出功率可表示成只与光照和温度有关的应变量。基于此，对于给定的光伏阵列，在不同的光照强度和温度条件下有对应于最大功率点的电压和电流，根据式（2）和式（3），可以求出不同自然条件下的最大输出功率为

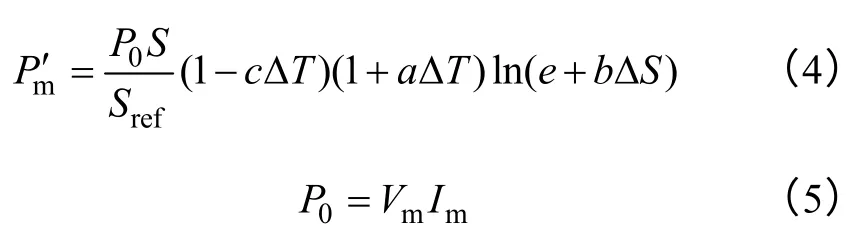
图1 所示为典型的含分布式电源（Distributed Generator，DG）配电网系统，Es为系统等值电动势，Zs、ZLl、ZL2和ZPV分别为系统等值阻抗、PCC 上游线路L1阻抗、PCC 下游线路L2阻抗和光伏电源滤波电路的阻抗，考察点接有一定负荷。

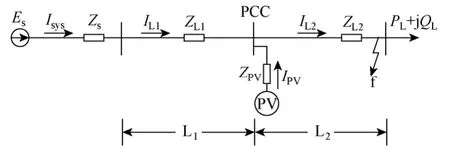
图1 含光伏电源的配电网系统接线图Fig.1 Single diagram of distribution network with PV power

由能量守恒定律：总功率等于输出功率、交流电路中的热效应加上器件的损耗，可得到

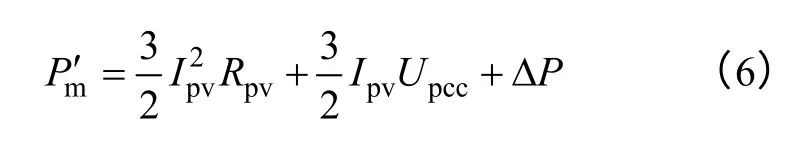
式中，Ipv为输出电流幅值；Rpv为光伏电源滤波电路的电阻值；Upcc为并网点电压幅值；ΔP相对很小，计算时可以近似忽略。根据式（4）～式（6）可求得系统的稳态等效电压Upv和输出电流Ipv为

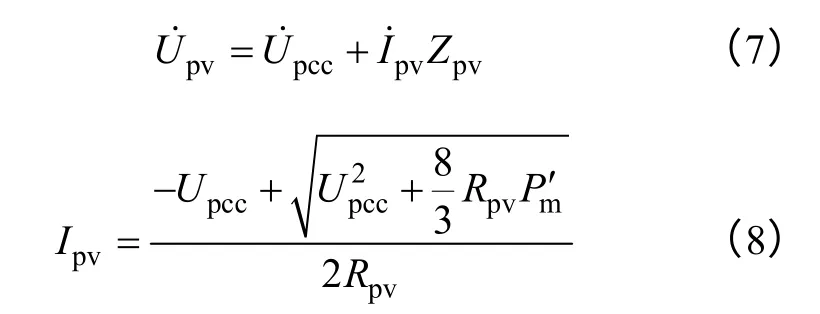
式中，以Upcc相位为基准，Ipv与其同相位。

3.2 暂态外特性

配电网中，故障切除时间通常小于1s，而光伏发电系统能量变化具有一定的惯性，因此在故障前后较短时间内系统捕捉的能量几乎保持不变。换言之，光伏发电系统的输出有功功率在故障前后不发生变化[20]。同时，配电网单相接地故障时允许继续运行。故本节将只对三相短路和两相相间短路故障时的暂态外特性进行研究分析。此外，根据光伏逆变器低电压穿越的要求及相关规定[21]，逆变器会配备低电压和过电流保护装置，但因本文研究对象为光伏发电系统的详细并网输出特性，故可忽略这些装置的影响，以获得最严重情况下的短路电流，从而进行最精确的分析。

3.2.1 三相短路

根据能量守恒，在短路发生后，通过逆变器的调节控制，输出电流在经过较短时间后达到稳定，此电流可通过联立方程组求得。

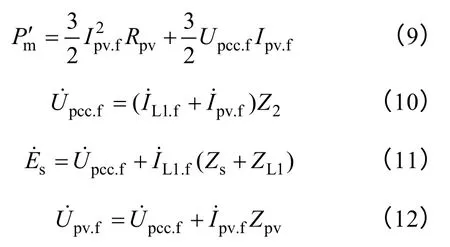
相对于电阻上的热效应与输出功率，光伏电源其他储能元件在短路前后储存能量的大小几乎没有变化，所以也可近似忽略不计。故可认为mP'为短路后的输出功率与滤波电路中电阻消耗的功率之和，Upcc.f和Ipv.f分别为短路后并网点电压和输出电流，Upv.f为等效模型的等效电压。由式（9）～式（12）可得

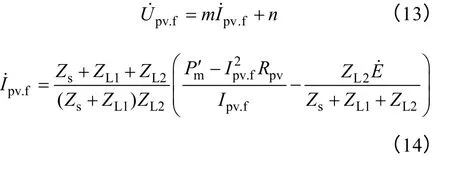
式中

3.2.2 两相短路

对称分量法是电力系统非对称故障分析与计算的主要方法，该方法利用系统正序、负序和零序等值网络所构成的复合序网，先计算各节点电压及各支路电流的序分量，再计算其三相值。下面以BC相间故障为例，研究故障后的稳态短路电流。根据文献[20]提供的方法，在传统控制策略下，两相短路后PCC 电压计算公式为

如果短路点不是位于光伏电源出口附近，短路前后滤波电阻上的损耗可近似认为不变。这样，就得到了PCC 电压和光伏电源的输出电流，根据电流与电压的关系，便可按式（18）求出等效模型中受控电压源的输出电压。

3.3 暂态过程分析

并网逆变器采用双闭环控制策略，其系统中内环的主要作用是跟踪外环输出的电流指令，提高系统的动态响应性能。逆变器并网运行时，由于闭环的作用，在不向系统提供无功支持的情况下，稳态时iq=0，动态过程中iq的变化也很小，并且内环的响应速度一般都远高于外环，所以内环可等效为一个惯性环节。

对于外环利用主导极点的概念使系统在允许的误差情况下也可进行降阶处理。为此，将系统其中两个极点配置为一对共轭极点并使之成为主导极点，另外一个极点配置在距离虚轴很远的地方。假设系统希望的闭环主导极点为，闭环非主导极点为s3=-nξωn，则期望的闭环特征方程为

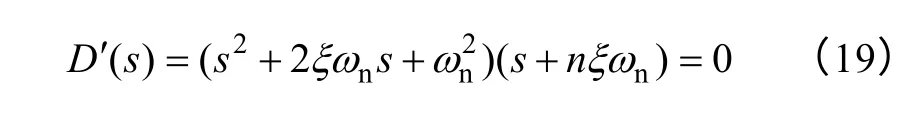
经分析，逆变系统的闭环特征方程为

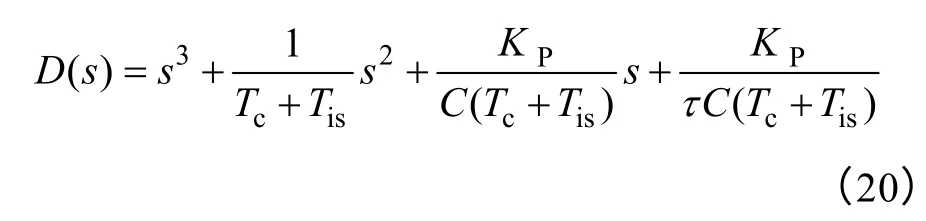
对比D(s) 与D'(s) 有

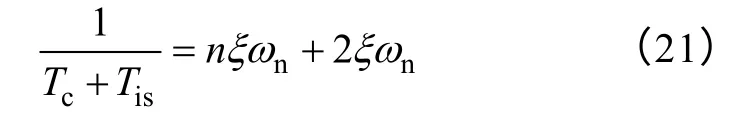
式中，Tis是等效为惯性环节的内环的时间常数；Tc为逆变器的开关周期，n一般取5～10，阻尼系数ξ按二阶系统最佳整定值取0.707 以达到最优控制效果，由n、ξ可求得ωn。最后根据自动控制理论原理，光伏发电系统的暂态过程便可用一个二阶振荡电路近似描述：

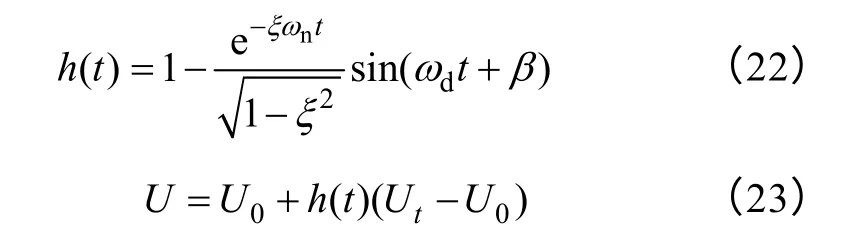
4 光伏发电系统等效模型设计

根据以上分析，对于给定的光伏发电系统，稳态情况下，光伏发电系统的输出电流取决于光照强度和电池温度；短路后，稳态短路电流还取决于短路点以及短路类型；暂态过程中的短路电流变化曲线取决于系统降阶后的阻尼比和自然振荡频率，主要由PI 参数决定。因此，等效模型可以设计为如图2 所示的电路。包括输入变量、函数模块、受控电压源、滤波阻抗和隔离变压器几部分。经过对输入变量的计算得出对受控电压源的控制信号，调节其输出电压的幅值和相角，经过滤波阻抗的滤波环节，将光伏发电系统的电流经隔离变压器输送到电网。隔离变压器的作用主要是提供安全的电压并起到保护和滤波的作用。

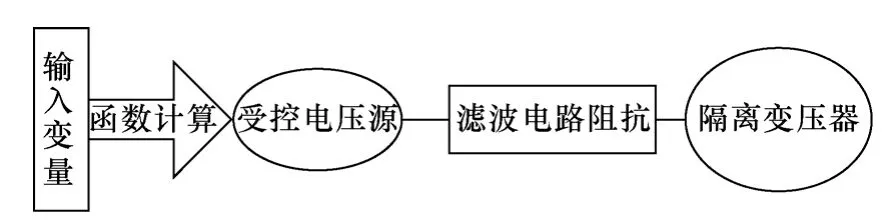
图2 等效模型主电路结构Fig.2 Equivalent model of the primary circuit diagram

等效模型中的函数模块以光照强度和温度作为输入量，根据式（4）和式（5）计算出不同自然条件下光伏发电系统的出力，同时根据式（7）和式（8）得到受控电压源的输出电压和与原详细模型相同的稳态输出电流。当电网故障时，以故障信息为输入量，并根据式（14）或式（17）计算出短路后的稳态短路电流，再与短路前的稳态输出电流一起，根据模型降阶的原理，通过三要素法便可计算出暂态过程中任意时刻的短路电流。最后，根据电压和电流的关系计算出对应的等效模型的输出电压。图3为函数模块的控制计算流程。所以，等效模型需要函数模块和接受其控制的受控电压源，还有与原电路相同的滤波电路和隔离变压器。这样就能使等效模型模拟出与原来详细模型相同的输出特性，使其对电网的影响也达到相同的效果。

图3 函数模块的计算流程Fig.3 Calculation process of function module

5 仿真分析

在 Matlab/Simulink 平台下搭建了光伏发电系统接入配电网的等效仿真模型，如图4 所示。光伏接入电网的额定电压为380V（线电压有效值）；光伏发电系统额定容量为 5.6kW，并网点电压为380V；线路L2所带负荷为(3.41+j0)kV·A；线路阻抗参数为：系统等值阻抗与线路 L1阻抗之和为(1+j2)Ω，PCC 下游线路L2阻抗为(0.5+j1)Ω。光伏等效模型的输入变量为时间、光照强度、温度及短路信息，经Rpv=0.5Ω，L=10mH 的滤波电路及隔离变压器（220V/380V）接入电网。其中①为函数模块，是整个模型的核心元件。在仿真开始前，通过设定相应的输入变量，使其在仿真时可计算出对②的控制量。②为受控电压源。③为与原详细模型中滤波电路相同的阻抗。为验证等效模型的有效性，本文还搭建了基于扰动观察法和双闭环控制的光伏发电系统详细模型。

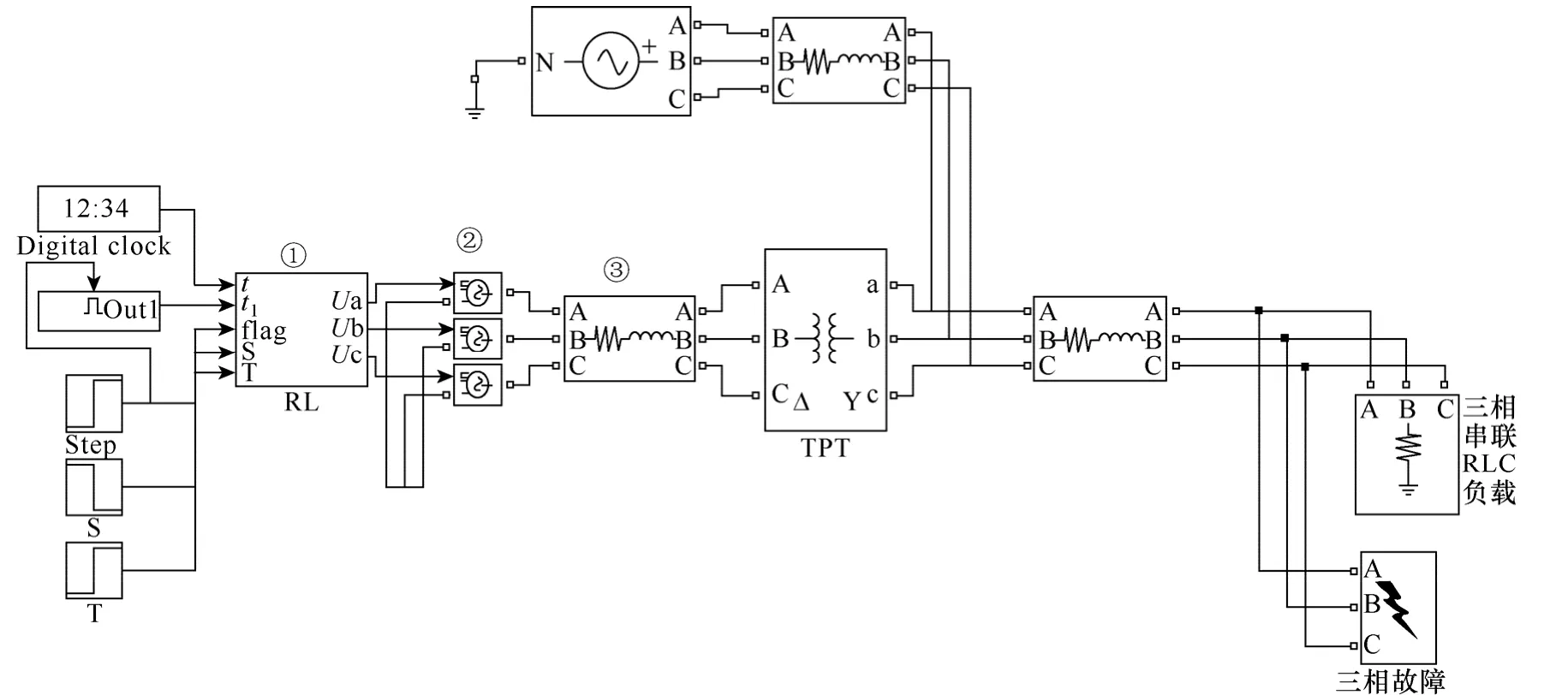
图4 光伏发电系统接入配电网的等效仿真模型Fig.4 Equivalent simulation model of photovoltaic system connected to the grid

5.1 不同气象条件下输出电流的对比

光伏发电系统的最大出力受气象条件影响较大，其输出的电流主要受到光照强度和温度的影响。为了对比不同气象条件下详细模型和等效模型的输出电流，分别针对相同温度、不同光照强度和相同光照强度、不同温度两种情况进行了仿真对比。结果见表1和表2。

分析表1和表2 可知，无论当温度相同光照强度变化时，还是光照强度相同温度变化时，等效模型的输出电流都略高于详细模型的输出电流，但相对误差都在5%以内。可见，在稳态情况下，无论气象条件如何变化，用等效模型替代详细模型，误差都满足工程计算的精度要求。分析稳态误差产生的主要原因，一方面是由于等效模型中不包含电力电子器件，从而降低了谐波含量，从而使基波输出电流稍高；另一方面，在等效计算过程中，由于采取近似计算与等效的方法，也会产生一部分误差。

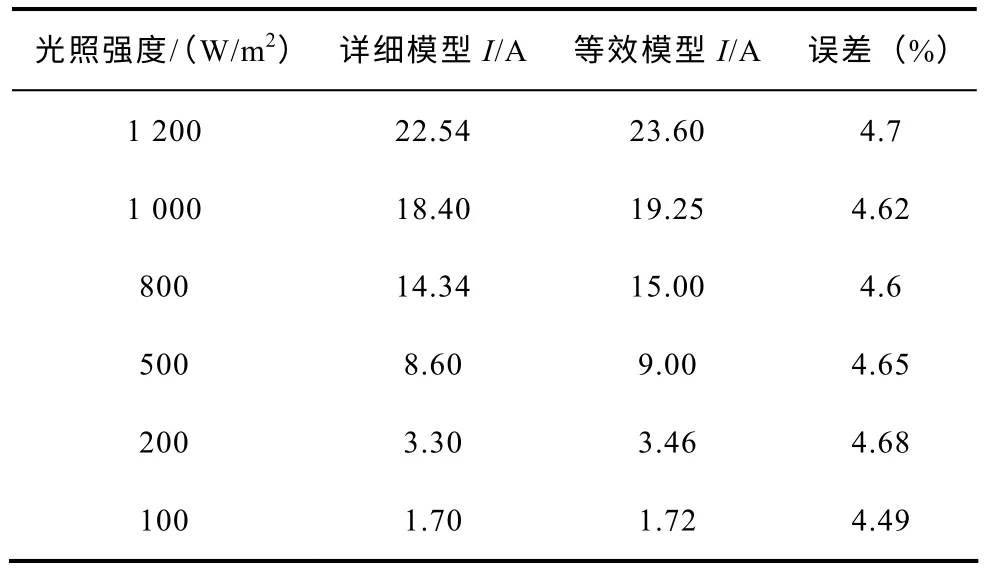
表1 温度25℃时详细模型与等效模型的输出电流Tab.1 The output current of detailed model and the equivalent model when the temperature is 25℃

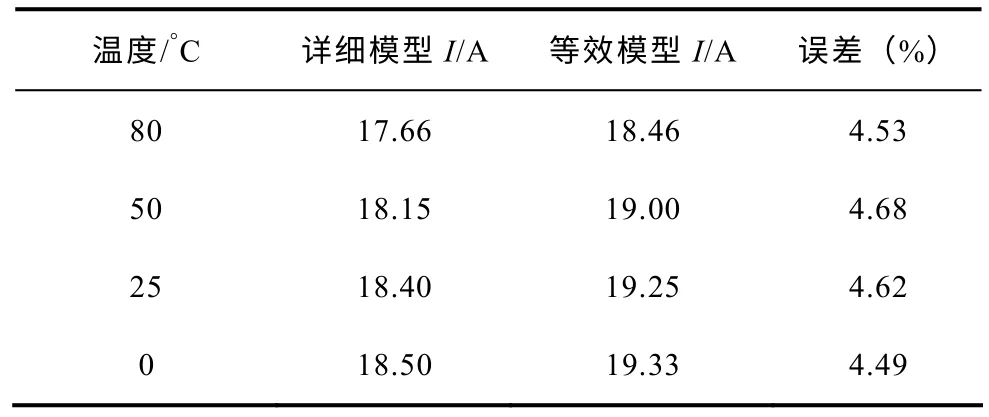
表2 光强1 000W/m2 时详细模型与等效模型的输出电流Tab.2 The output current of detailed model and the equivalent model when the light intensity is 1 000W/m2

5.2 动态过程中短路电流的对比

为了分析动态过程中等效模型的有效性，仿真了在线路L2末端处1s 时发生短路的情况。三相短路电流波形如图5 所示，BC 两相短路电流波形如图6 所示，短路电流幅值见表3。

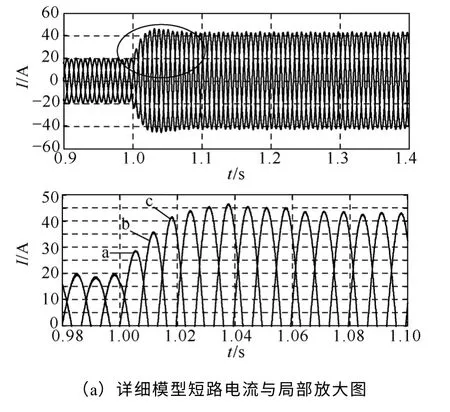
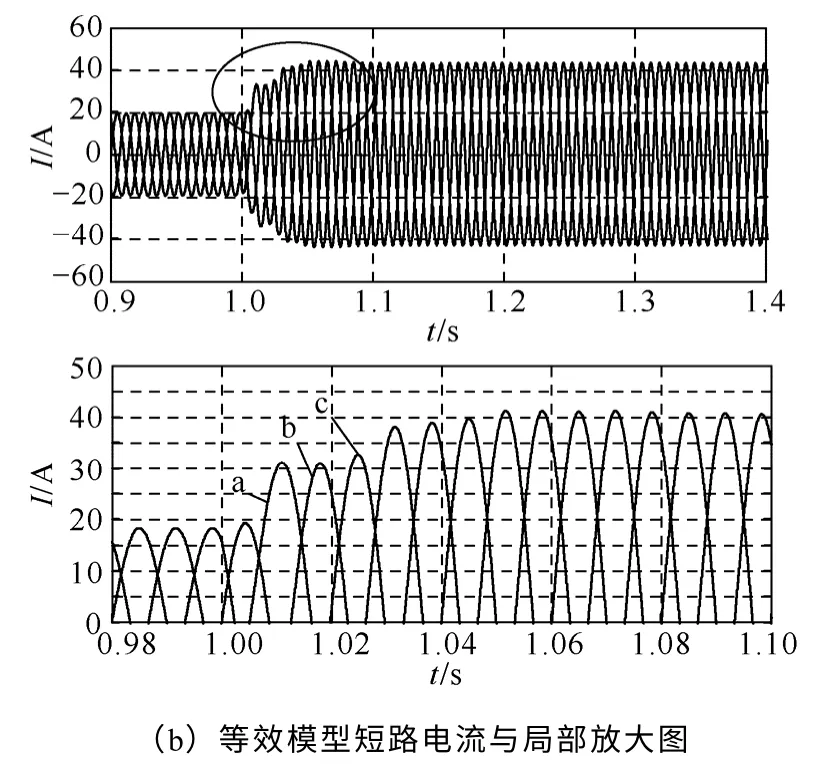
图5 三相短路电流暂态过程Fig.5 The transient process of three-phase short-circuit current

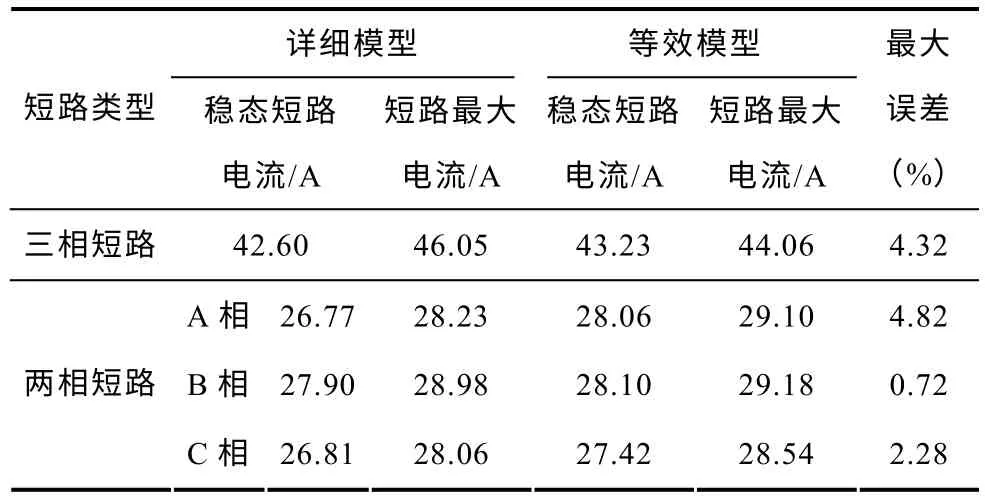
表3 详细模型与等效模型的短路电流Tab.3 Short-circuit current of detailed model and the equivalent model

分析表3 可知，在三相短路情况下，等效模型的稳态短路电流较详细模型略高；暂态过程中，详细模型的短路最大电流略高于等效模型，但相对误差均小于5%。除此之外，发生两相短路后，在不对称运行条件下，A 相短路电流相对误差最大，C相次之，B 相最小；同样，暂态过程中，电流上升曲线也略有偏差，但相对误差仍在5%以内。可见，在暂态情况下，用等效模型替代详细模型，误差满足工程计算的精度要求。

分析暂态情况下产生误差的主要原因有以下几方面：①采用了对传递函数近似降阶的方法，而且此过程忽略了直流侧和接入的配电网及其运行状况对传递函数的影响。传递函数的偏差，导致暂态过程中两个模型中故障电流的时域特性的差异；②详细模型的稳态电流误差的影响；③忽略掉了逆变器的电力电子器件，其特性误差也会产生误差。总之，等效模型通过近似和等效，忽略了一些影响相对较小的“中间环节”与次要项，从而导致了输出的相对误差，但相对误差均在5%以内，所以用等效模型替代详细模型误差满足工程计算的精度要求。

此外，在电压和有功、无功功率方面，简化模型的输出与详细模型相比也极相近，可以满足工程计算的精度要求。在计算效率方面，采用同一台计算机，仿真时长设置为2s，使用详细模型和等效模型仿真所需的时间分别为 166.806 2s和44.455 8s（联想 Y470，处理器型号：Intel(R) Core(TM)i3-2350M CPU @ 2.30GHz，内存4GB）。经对比可知，使用等效模型的仿真效率将近为使用详细模型的4 倍，可大大提高仿真计算的效率。究其原因，是因详细模型为包含电力电子器件的高阶系统，仿真过程需要进行大量复杂的计算；而与之相比，等效模型不包含电力电子器件的一阶系统，仿真过程只包含少量的简单公式计算。

6 结论

通过对光伏发电系统的稳态暂态外特性进行研究分析，提出了一种基于电气外特性的光伏发电系统等效模型建模方法。该等效模型只需要以光照强度、温度和故障信息作为输入量，通过计算出其故障前后的稳态电流和设置二阶动态特性相关参数，进而可拟合出与详细模型相同的输出特性，所以在仿真过程中无需迭代。仿真分析表明，与详细模型相比，采用该模型无论在稳态和暂态情况下，其输出电流误差都在5%以下，计算效率则提高了近4倍。虽然与使用详细模型仿真相比，需要将故障信息作为输入量，并计算出短路前后的稳态电流。但由于配电网结构较为简单，多为辐射网，所以计算量较小，相对于需要多次迭代的详细模型仍然能够很大程度减小计算量，所以此模型具有一定的工程实用价值。

新的光伏逆变器标准[21]要求大型光伏逆变器应具有故障穿越的要求，这种情况下发生三相、两相或单相短路，其电气输出特性会发生变化。而针对基于新标准下的光伏发电系统，其模型需作相应改进，主要需进行控制方法的更新，进行重新建模和大量仿真计算，其最终的简化模型也必将产生变化，将是本课题组下一步继续研究的问题，将在今后的论文中进行报道。

[1]Zobaa A F,Cecati C.A comprehensive review on distributed power generation[C].International Symposium on SPEEDAM,Taormina,Italy,2006:462-469.

[2]Carrasco J M,Franquelo L G,Bialasiewicz J T,et al.Power-electronics systems for the grid integration of renewable energy sources:a survey[J].IEEE Transactions on Industrial Electronics,2006,53(4):1002-1016.

[3]苏建徽,余世杰,赵为,等.硅太阳能电池工程用数学模型[J].太阳能学报,2001,22(4):409-412.Su Jianhui,Yu Shijie,Zhao Wei,et al.Silicon solar cell engineering model[J].Acta Energiae Solaris Sinica,2001,22(4):409-412.

[4]孙自勇,宇航,严干贵,等.基于PSCAD 的光伏阵列和MPPT 控制器的仿真模型[J].电力系统保护与控制,2009,37(19):61-64.Sun Ziyong,Yu Hang,Yan Gangui,et al.PSCAD simulation models for photovoltaic array and MPPT controller[J].Power System Protection and Control,2009,37(19):61-64.

[5]姚致清,张茜,刘喜梅.基于 PSCAD/EMTDC 的三相光伏并网发电系统仿真研究[J].电力系统保护与控制,2010,38(17):76-81.Yao Zhiqing,Zhang Qian,Liu Ximei.Research on simulation of a three-phase grid-connected photovoltaic generation system based on PSCAD/EMTDC[J].Power System Protection and Control,2010,38(17):76-81.

[6]李冬辉,王鹤雄,朱晓丹,等.光伏并网发电系统几个关键问题的研究[J].电力系统保护与控制,2010,38(21):208-214.Li Donghui,Wang Hexiong,Zhu Xiaodan,et al.Research on several critical problems of photovoltaic grid-connected generation system[J].Power System Protection and Control,2010,38(21):208-214.

[7]刘邦银,段善旭,刘飞,等.基于改进扰动观察法的光伏阵列最大功率点跟踪[J].电工技术学报,2009,24(6):91-94.Liu Bangyin,DuanShanxu,Liu Fei,et al.Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J].Transactions of China Electrotechnical Society,2009,24(6):91-94.

[8]傅诚,陈鸣,沈玉梁,等.基于输出参数的最大功率点控制[J].电工技术学报,2007,22(2):148-152.Fu Cheng,Chen Ming,Sheng Yuliang,et al.A control method of maximum power point based on output parameters[J].Transactions of China Electrotechnical Society,2007,22(2):148-152.

[9]Kuo YeongChau,Liang TsorngJuu,Chen JiannFuh.Novel maximum power point tracking controller for photovoltaic energy conversion system[J].IEEE Transactions on Industrial Electronics,2001,48(3):594-601.

[10]Toshihiko Noguchi,Shigenori Togashi,Ryo Naka*moto.Short-current pulse-based maximum power point tracking method for multiple photovoltaic and converter module system[J].IEEE Transactions on Industrial Electronics,2002,49(1):217-223.

[11]刘波,杨旭,孔繁麟,等.三相光伏并网逆变器控制策略[J].电工技术学报,2012,27(8):64-70.Liu Bo,Yang Xu,Kong Fanlin,et al.Control strategy study for three phase photovoltaic grid-connected inverters[J].Transactions of China Electrotechnical Society,2012,27(8):64-70.

[12]Dou W,Xu Z,Peng Y,et al.Current controller optimum design for three-phase photovoltaic gridconnected inverter[J].Transactions of China Electrotechnical Society,2010,25(8):85-90.

[13]胡雪峰,谭国俊.SPWM 逆变器复合控制策略[J].电工技术学报,2008,23(4):87-92.Hu Xuefeng,Tan Guojun.The multiple control strategy for SPWM inverter[J].Transactions of China Electrotechnical Society,2008,23(4):87-92.

[14]耿攀,吴卫民,叶银忠,等.基于重复控制的单相分时复合级联光伏逆变器控制[J].电工技术学报,2011,26(3):116-122.Geng Pan,Wu Weimin,Ye Yinzhong,et al.Singlephase time-sharing cascaded photovoltaic inverter based on repetitive control[J].Transactions of China Electrotechnical Society,2011,26(3):116-122.

[15]李广凯,李庚银,梁海峰,等.基于电压源换流器的光伏并网系统暂态特性研究[J].太阳能学报,2007,28(7):715-720.Li Guangkai,Li Gengyin,Liang Haifeng,et al.Research on dynamic characteristics of VSC based photovoltaic grid-connected system[J].Acta Energiae Solaris Sinica,2007,28(7):715-720.

[16]Rodriguez P,Timbus A V,Teodorescu R,et al.Flexible active power control of distributed power generation systems during grid faults[J].IEEE Transactions on Industrial Electronics,2007,54(5):2583-2592.

[17]章玮,王宏胜,任远,等.不对称电网电压条件下三相并网型逆变器的控制[J].电工技术学报,2010,25(12):103-110.Zhang Wei,Wang Hongsheng,Ren Yuan,et a1.Investigation on control of three-phase grid-connected inverters under unbalanced grid voltage conditions[J].Transactions of China Electrotechnical Society,2010,25(12):103-110.

[18]袁旭峰,程时杰,文劲宇.改进瞬时对称分量法及其在正负序电量检测中的应用[J].中国电机工程学报,2008,28(1):52-58.Yuan Xufeng,Cheng Shijie,Wen Jinyu.An improved method of instantaneous symmetrical components and its detection for positive and negative sequence current[J].Proceedings of the CSEE,2008,28(1):52-58.

[19]Singer S,Bozenshtein B,Surazi S.Characterization of PV array output using a small number of measured parameters[J].Solar Energy,1984,32(5):603-607.

[20]吴争荣,王钢,李海锋,等.含分布式电源配电网的相间短路故障分析[J].中国电机工程学报,2013,33(1):130-136.Wu Zhengrong,Wang Gang,Li Haifeng,et al.Analysis on the distribution network with distributed generators under phase-to-phase short-circuit faults[J].Proceedings of the CSEE,2013,33(1):130-136.

[21]国家能源局.光伏发电并网逆变器技术规范[Z].2013-3-7.