一种基于试验数据的动态辨识建模方法及应用*
(92337部队 大连 116023)
1 引言
开展复杂边界条件下的装备试验和应用研究,完成潜艇在体系作战能力中的使用性能评估,是使用试验工程研究的重点之一。由于潜艇外场试验试验成本高,限定了其次数和规模,造成试验需求和试验能力之间的矛盾,尤其对于多任务剖面下的潜艇使用试验,外场试验更是受到极大限制。要解决这些瓶颈问题,只有将建模仿真技术大规模应用到潜艇使用试验鉴定工作中。因此,如何构建置信度较高的潜艇模型体系包括机动模型、探测模型、武器模型等成为课题的关键所在。
传统的机理建模方法,模型原理复杂,涉及参数多且需要通过特定试验测量或理论计算,不仅置信度和精度存在严重局限性,在工程应用中也难以掌握。与此相比,潜艇装备使用试验测控得到海量数据,如何从蕴含着大量信息的数据中挖掘各变量之间的规律,确定严重非线性复杂对象众多参数值,成为目前基于试验数据建模的研究难点。
对于严重非线性的复杂对象建模问题,目前有数种不同的非线性模型结构以及相应的数据驱动的建模方法,包括神经网络技术[1]、决策树学习[2]、具有外部输入的非线性自回归滑动平均模型以及小波网络模型[4]等。这些方法各有所长,但是这些方法存在着待定参数过多、模型结构难以确定等问题,如果所关注对象是一个高维空间问题,往往还会陷入“维数灾难”的状况。因此,这些方法的应用效果与使用者的经验有很大的关系,特别是所关注对象很复杂时,这种依赖就更强。在实际使用中,要想获得高精度的估计,使用者需要消耗大量的时间和精力来选择恰当的建模方法,确定合适的模型结构或者模型集合,同时还需要对算法和参数进行反复调整。
文章提出一种动态辨识建模方法,实现了基于搜索、聚类和分类技术的非线性离散系统的集成动态建模。该方法将人工智能和机器学习领域中的一些技术应用到动态系统辨识领域中,以模型参数的经验协方差矩阵作为性能指标,在状态输入空间中进行搜索并聚类,在对获得的聚类进过反复调整后,采用分类技术将状态输入空间划分为不同的区间,在每个区间上建立一个仿射模型。通过该方法可以有效提升低精度、简单算法的泛化性能,解决复杂非线性对象或者高维对象建模精度低,进一步分析和预测难的难题。
2 非线性离散对象的建模问题描述
令F:x→RP为定义在x⊆Rn上的一个非线性映射,给定样本集:

其中数据点满足

其中ε(k)∈RP是干扰项。给定性能指标为Vn=目标是找到一个PWA 映射使得性能指标最小。

其中θi∈R(n+1)×p,i=1,…,s是模型参数矩阵,而是由超平面分割开的X的面角区间。满足且当i≠j时有Xi∩Xj=∅。
对于动态系统辨识问题,上式中的k就代表时间序列。x(k)是回归向量,定义如下:

其中u(k)∈Rm表示系统的输入,y(k)是系统的输出。na和nb是模型的阶次,n=na×p+nb×m。
3 辨识算法
3.1 数据点的初步聚类
一般情况下用来自相同子模型的数据点辨识得到的模型参数比来自不同子模型的数据点辨识得到的模型参数具有更高的置信度,这是因为前者只与噪声有关而后者还要受到模型不一致的影响。参数的置信度较高具体表现为模型参数的经验协方差矩阵(绝对)值较小。因此可以利用模型参数的协方差矩阵值作为性能指标,在样本数据点中进行搜索,得到数据点的初步聚类。为了有效区分具有相同子模型参数但处于不同区间上的数据点,还需要在初步聚类过程中加入距离参数进行约束,以保证具有相似子模型参数但实际上分属不同区间中的数据点被归入不同的聚类中。具体算法1如下所示:

采用最小二乘法估计出新的模型参数和新的参数协方差矩阵,计算新老协方差矩阵的差

S0=S0∪S,并令S=0
3.2 数据点聚类的调整
通过3.1的初步聚类,大多数数据点都被正确聚类,但还是存在一些数据点不属于任何一个聚类,也会有一些数据点被错分或者出现错误聚类的情况。另外,还可能出现同一个区间上的数据点被分割到不同聚类中,而这些聚类具有相似的模型参数。因此本节对3.1节中得到的初步聚类结果进行调整,已解决上述问题。
第一步:首先解决相同区间上的数据点被归入不同聚类中的情况。假设经过初步聚类后共获得J个类别,从中任意挑选两个聚类Ck和Cl进行比较。为了保证那些具有相同模型参数,但部分不在不同区间的聚类不会被合并,同样需要引入一个距离参数dmin,用来衡量聚类之间的距离如算法2所示:
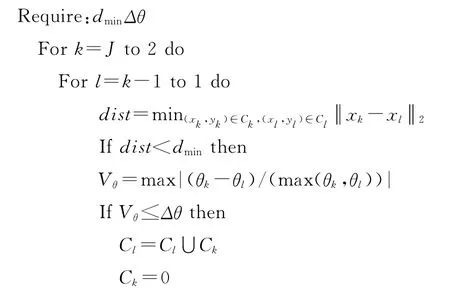
采用最小二乘法估计出新的模型参数和新的参数协方差矩阵Vl
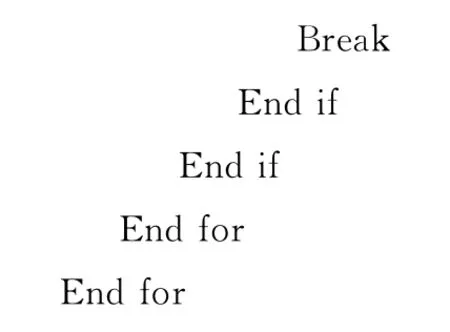
第二步:然后要将S0中的未分类数据点分配到各个聚类中。对于S0中数据点的分配,是根据它的c-1个邻近分类情况做决定的,详见算法3。

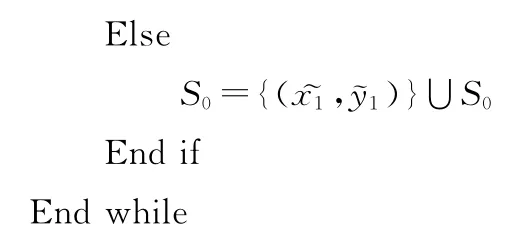
第三步:当每个数据点都属于某一聚类之后,就需要对数据点的聚类进行细调,要将错误分类的数据点归入正确的聚类中,详见算法4。

第四步:最后需要对所有的聚类进行细调,删除包含数据点过少的聚类,并将其中的数据点归入其它聚类中。如算法5所示,对每个聚类逐一进行检查。如果某个聚类中所包含的数据点少于c,则解散该聚类,并将其数据点放入S0中。对于S0中的那些数据,再通过算法5进行分类。

3.3 区间分割和子模型的辨识
接下来根据调整后的数据点聚类进行回归向量空间的区间分割,这实际上是一个有监督的模式分类问题,可采用线性支持向量机(LSVM)[3]来完成这个步骤。文章所采用的SVM 函数来自基于Matlab仿真平台的spider软件包,其核心就是由LIBSVM[4]软件实现的。
最后,对不同的数据区间采用加权最小二乘算法等线性辨识方法,得到每个区间上的子模型参数。
4 应用实例
在海量航行试验数据基础上,构建潜艇强机动上浮的稳性与操纵性边界分析模型。
输入:航速U、纵倾θ
指定:围壳舵或尾升降舵舵角,δb围壳舵0°~25°,δs尾升降舵0°~30°,一般取围壳舵25°满舵。
输出:

通过动态辨识算法,得出模型中的三个扰动参数(a、b、c)。
在确保安全的前提下,以5°、7°、10°和10kn、12kn为试验因子进行试验设计,确定了水下X1m尾倾Y1°航速Z1kn上浮试验,水下X2m 尾倾Y2°航速Z2kn上浮试验,水下X3m 尾倾Y3°航速Z3kn上浮试验,水下X4m 尾倾Y4°航速Z4kn上浮试验共四项试验。
选取其中包含50 个数据点的样本集,如图1所示。
1)原始数据集
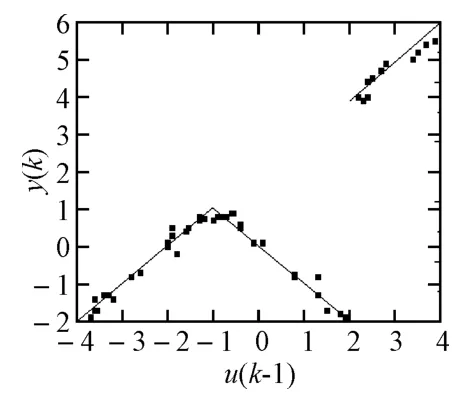
图1 原始数据集

图2 应用算法1后的聚类结果
2)数据点初步聚类
通过上述辨识算法,得到如图2所示的聚类结果。一共得到四个数据点聚类,分别用●、○、■、□不同图形标识。△方块不属于任何一个聚类。
3)数据点聚类调整及区间分割和子模型辨识
经过数据点聚类调整及区间分割和子模型辨识后可以得到如图3所示的聚类结果。
根据以上三个聚类,任意选取其中的两个聚类,用线性支持向量机(LVSM)方法进行分类,获取其分割平面。采用的支持向量机函数来自于与基于Matlab仿真平台的SPIDER 软件包,其核心就是由LIBSVM 软件实现的。

图3 应用算法2~5后得到的聚类结果
如此重复三次,可得三个区间分割。最后通过加权最小二乘方法,对每个区间上的数据点进行参数拟合,最终得到潜艇强机动上浮操纵性边界分析模型。
5 结语
从上述实例可以看出,该方法在搜索以及调整过程中会自动得到聚类,因此不需要预先指定子模型的数量,并且还能有效重构具有相同模型参数但处于不同区间上的子模型。由于算法本身是针对有噪声的情况提出的,因此本方法对噪声具有一定的鲁棒性。
[1]张志华,郑南宁,赵振选.基于模糊对向神经网络的非线性动态系统辨识器[J].控制理论与应用,2009,17(4):565-568.
[2]T.M.Mitchell.机器学习[M].北京:机械工业出,2003:100-127.
[3]胡玉玲,曹建国.基于模糊神经网络的动态非线性系统辨识研究[J].系统仿真学报,2007,19(3):560-562.
[4]M.Prandini.Piecewise affine system identification:A learning theoretical approach[C]//Bahamas:In Proceedings of the 43th IEEE Conference on Decision and control,2004:3844-3849.
[5]于玲.基于数据的复杂系统集成建模方法及其应用研究[D].杭州:浙江大学,2006:53-75.
[6]赵丽,李天舒,刘玉蕾.基于支持向量机的机器学习的研究[J].哈尔滨师范大学自然科学学报,2008,24(6):56-59.
[7]沈永欢,梁在中,许履瑚,等.实用数学手册[M].北京:科学出版社,2006:15-70.
[8]边肇祺,张学工.模式识别[M].北京:清华大学出版社,2000:78-90.
[9]V.Vapnik.统计学习[M].理论研究,2003:67-110.
[10]张智,朱齐丹,邢卓异.基于SVM 的大样本集系统辨识与函数拟合仿真[J].计算机仿真,2009,23(9):125-128.
[11]杨浩,项丹,冯树辉,等.基于直接接分最小二乘法的同步发电机的参数辨识[J].湖南大学学报(自然科学版),2013,40(7):69-73.

