弹丸侵彻深度算法研究＊

（92060部队 大连 116041）

1 引言

目前计算弹体对岩石和混凝土等靶标材料的侵彻深度公式不下40种［1］，各种公式方法互不相同，千差万别，每个经验公式都有各自的应用范围和应用条件，最终的计算结果也肯定存在一定的差别，对于土体等软弱介质的侵彻深度经验公式比较成熟，各个经验公式的计算结果精确度较高，而对于岩石和混凝土等脆性固体介质的侵彻深度经验公式就不够理想［2］，在众多的复杂的侵彻深度公式中，真正应用较广且精度较高的公式并不多。应用较广且精度较高的混凝土侵彻深度计算经验公式，它们的缺点就是经验公式计算侵彻深度与靶体材料参数有关，当公式中变量发生变化的时候，无法知道材料的属性就无法精确计算出弹体的侵彻深度。

2 常用的侵彻深度计算经验公式

弹体侵彻深度预估是研究弹体侵彻效应的重要内容之一，由于对弹体在侵彻过程中的受力机制并不清楚，加之混凝土高应变率结构关系的复杂性，目前还无法得到侵彻深度的解析解。工程上所采用的混凝土、岩石等侵彻深度计算公式属于经验公式，每个经验公式都是以大量试验数据为基础建立起来的，具有一定的经验性和应用范围。

目前应用较广且可信度较高的公式由美国Sandia国家重点实验室与美国陆军工程兵水道试验站（WES）提供WES公式，表达式为

式（1）中，H为侵彻深度（m），M为弹体质量（kg），v0为撞击速度（m／s），A为弹体横截面积（m2），ρ为混凝土密度（kg／m3），NIC是弹头性能参数，对于锥形弹头；NIC＝0．805 sin（η）0．5（η是弹头的半锥角）；YIC＝Y（RQD／100）0．2：Y为混凝土靶的无约束压缩强度（Pa），RQD为岩石和混凝土品质指标，一般认为20＜RQD＜100。

WES公式用三个参数反映靶体的特性，包括岩体质量系数，岩石无侧限强度和岩体质量密度，一定程度上考虑了现场靶体介质的不连续性。公式中参数意义较明确，容易确定，对于计算弹体在岩石和混凝土介质的侵彻深度精度较高。

美国Snadia国家重点实验室于1960年开始研究土中侵彻，进行了约3000次试验，建立了重要的试验数据库，1967年提出了根据其试验数据建立的基本经验公式，即Snadia 土中侵彻公式［3］。Young基于新的试验数据对公式进行了多次修正，得出了侵彻土、岩石、混凝土统一的经验公式，最近的1997年Young公式［4］。

式（2）中，H为侵彻深度（m），M为弹体质量（kg），v0为弹体着靶速度（m／s），A为弹体横截曲积（m2）。卵形弹头，锥形弹头N＝0．56＋0．25Ln／d，Ln为弹头长度（m），d为弹体直径（m），rCRH为弹头系数，S为阻力系数，fc为混凝土无侧限抗压强度（MPa），Ke＝（F／W1）0．3，W1为靶体宽度与弹体直径的比值。如果W1＞F，则Ke＝1，对于薄板，F减少一半；P为混凝土体积配筋率；Q为岩石质量指标；tc为混凝土浇筑时间（年），取tc＞1 时，tc为靶体厚度与弹体直径的比值，05≤tc≤6；若无试验资料根据，可取S＝09。如果M≤182kg，则侵彻深度乘以修正折减系数Ke＝0．46M0．15。

在美国陆军《抗常规武器设计规范》中，建议采用如下经验公式计算弹体侵彻钢筋混凝土深度［5］：

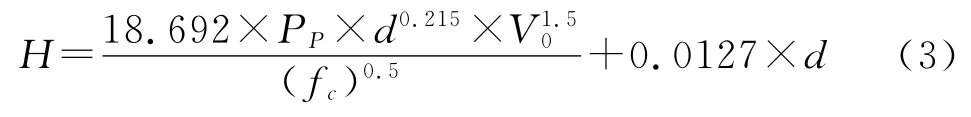
式（3）中，H为侵彻深度（m），pp为弹体截面荷载（kg／m2），等于弹体质量与弹体横截面面积之比；fc为混凝土抗压强度（Pa），d为弹体直径（m）。

在我国，一般采用如下的弹体侵彻深度计算公式［6］：

式（4）中，H为侵彻深度（m），λ1为弹形修正系数，P为弹体质量（kg），d为弹体直径（m），Kd为反映介质特性的实验系数，V0为弹体着靶速度（m／s）。该式假定侵彻阻力与炮弹在介质中运动速度与炮航弹横截面面积成正比，通过试验确定有关系数．试验是在特定的靶体和特定的弹种以及特定的侵彻速度条件下进行的，各种条件都带有一定的局限性。在原型实弹试验中所用的弹径在0．075m～0．203m 之间，超出这个范围就要进行修正。

在上述公式中，WES公式、Young公式、美国陆军公式和我国的弹体侵彻深度计算公式虽然在工程中大都得到了广泛的应用，但是它们的缺点就是经验公式计算侵彻深度与靶体材料参数有关，当公式中变量发生变化的时候，无法知道材料的属性就无法精确计算出弹体的侵彻深度。

3 由着速和侵彻加速度计算侵彻深度

3．1 算法原理

图1 侵彻原理示意图

在弹体侵彻硬目标时，弹体受到的阻力方向与速度方向相反，战斗部将获得很大的轴向负加速度如图1所示。

垂直于侵彻靶体建立坐标系，列出弹体运动学方程，得出侵彻t时刻的子弹轴向速度v（t）和垂直侵彻深度h（t）为

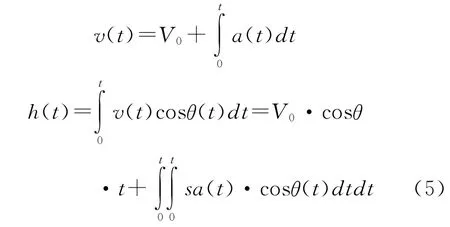
式中，V0为弹体着靶初速，a（t）为侵彻t时刻弹体受到的轴向加速度，θ为弹体着靶时与侵彻靶体着角，θ（t）为弹体侵彻角（弹轴与垂直侵彻深度h的夹角）。弹体侵彻深度是弹丸着角、着速、侵彻角、侵彻加速度值的函数。

3．2 算法分析

式（5）相对比较复杂，通过对侵彻过程作合理假设：

1）弹体为刚体，侵彻中无较大变形。

2）弹速方向与弹体轴线方向一致。

3）弹体在目标中是直线运动。

4）弹体着靶初速已知。

如果弹体变形很大，弹体的动能将有损失。而弹形的破坏可能导致运行轨迹难以跟踪。攻角决定了弹体着靶的姿态，对于侵彻钻地弹该条件较易满足。

在此假设的基础上，弹轴与垂直侵彻深度h的夹角θ（t）即为固定角弹体着角θ，式（5）可以改写成如下

如果是计算弹丸侵彻行程，则式（6）改写成如下

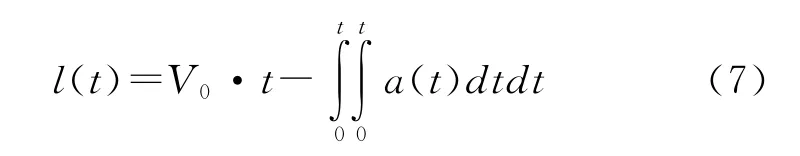
本文按式（7）讨论，通过在子弹轴向安装高g值加速度传感器获取子弹侵彻靶体实时加速度，子弹着靶初速通过查询预先装订在引信系统中的数据获取，实时计算侵彻行程。通过A／D 把模拟的侵彻加速度信号转化为离散数字信号，设A／D 采样周期为Tc，则在A／D转换第i次ti时刻，采用简单的梯形积分法求速度v（ti）和行程l（ti），有：

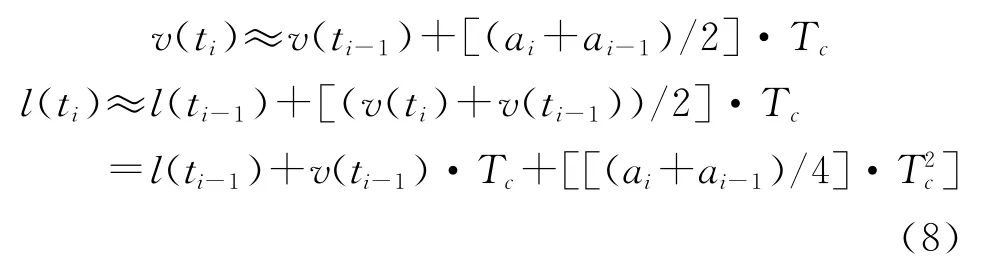
式（8）中，ai为ti时刻A／D转换的数字量，v（ti-1）为ti-1时刻弹体轴向速度，l（ti-1）为ti-1时刻弹体侵彻行程。速度v（ti-1）和行程l（ti-1），可以由A／D第一次转换类推，而T1＝Tc：

式（9）中，a1为A／D第一次转换结果，V0为弹体着靶初速由数据库给定。

有了侵彻过程任意ti时刻的侵彻加速度ai、速度v（ti）和行程l（ti），就可以根据不同的起爆要求，确定不同的起爆准则。如：

1）弹丸对复合层目标结构的侵彻遵循图2所示曲线的规律［7］。

图2是某弹丸侵彻土壤／混凝土复合结构层的侵彻减加速度时间历程曲线；其中Oac段是弹丸侵彻复合层中土壤部分的侵彻减加速度时间历程曲线，bcd段是弹丸侵彻土壤后直接侵彻混凝土的侵彻减加速度时间历程曲线，由该曲线可知，弹丸对复合结构层的侵彻满足：微处理器通过对侵彻信号的判断，就能识别不同的介质，从而达到智能起爆的目的［8］。

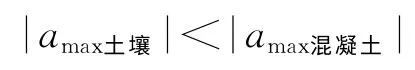
2）弹丸对有多层和带间隙的目标结构，弹丸的侵彻加速度时间历程如图3所示。

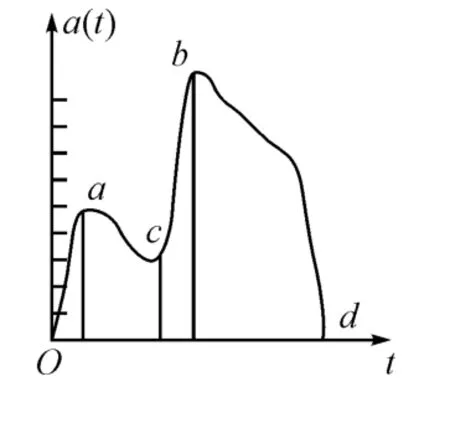
图2 弹丸侵彻复合层结构的加速度时间历程曲线

图3 弹丸侵彻带间隙的某双层钢板侵彻加速度时间历程曲线

图3中oabc段、de段、degf段分别是弹丸侵彻第一层目标介质、间隙和侵彻第二层目标介质的加速度时间历程曲线。由此可见，可利用一门限值很低的比较器和计数器来“识别”侵彻的间隙及间隙数并进一步推算侵彻的层数。由上面的分析可知，用弹丸侵彻加速度时间历程曲线中的特征参数amax的大小和持续时间可直接判断弹丸所侵彻的介质类型，用图3中a（tc）或a（td）的值作为间隙“识别”比较器的门限值和一宽度为t＜tc-td的时间窗就可判断出侵彻行程中穿过的间隙数和层数。如要求穿透一层目标后起爆。则只要给定一足够小的加速度值am，当ak≥am的时刻tk即为起爆时刻。要求穿透一层目标后再飞行一段距离Lx后起爆。如果弹体穿透一层目标后的瞬时速度为vc，由于弹体穿透目标后在空中飞行时，速度快而空气阻力相对来说很小，因此可近似看作匀速运动。则只要在上述时刻tk再延时tc后起爆即可。而tc＝Lx／vc。如果要求侵彻一定行程后起爆，则只要满足下列条件即可：ll≥L，ll为微处理器在tl计算的侵彻行程，tl起爆即可。

3．3 算法归一化处理

式（9）中，计算ti时刻的侵彻行程，微处理器要作乘法运算。乘法运算对于微处理器来说，相对加法运算耗时长［9］。如果对式（9）作相应转换，得式（10）。

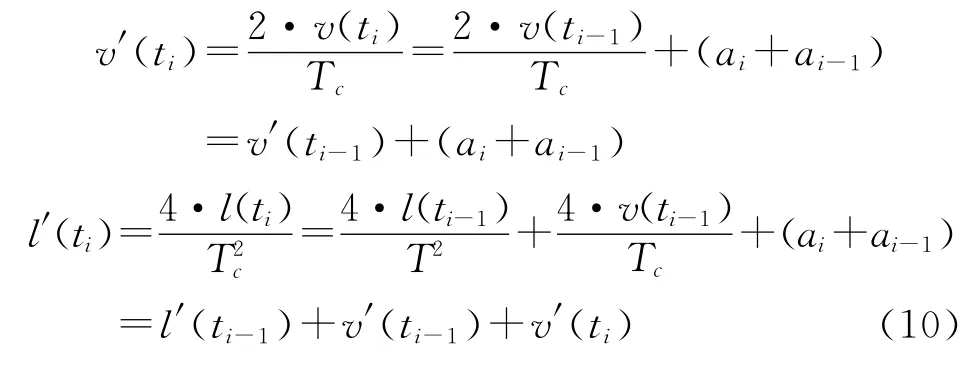
通过对式（10）的转换，得式（11）：

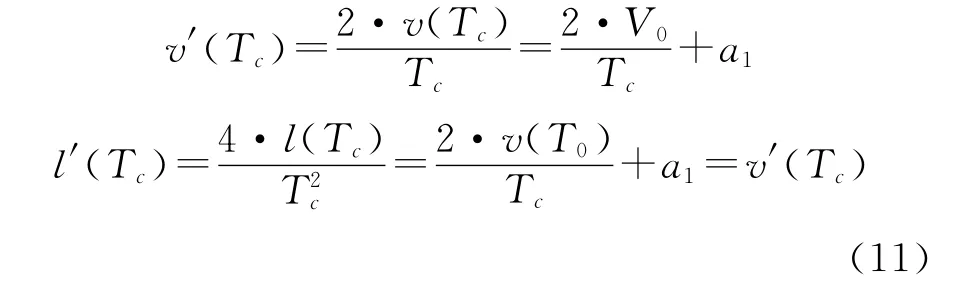
即可得到ti时刻的v′（ti）和l′（ti）。由式（10）和式（11）可以看出，通过简单的加法运算即可计算v′（ti）和l′（ti），极大提高了微处理器计算侵彻行程的效率。对给定的着靶初速启和预定起爆行程L作如下处理

避免了通过l′（ti）计算实际行程l（ti）。因为计算实际行程要实时通过式（13）

微处理器每计算一次l（ti）都要作式（13）处理，再与L比较。而通过对数据库着靶初速V0和预定起爆行程处理L作式（12）处理后。微处理器通过对l′（ti）与L′的比较，即可得到在预定行程L的起爆时刻，提高了微处理器处理效率［10］。

4 结语

本文介绍了几个目前应用较广的混凝土侵彻深度计算经验公式，并就各个公式的应用范围进行讨论，最后分析了由弹体着靶初速和侵彻加速度计算侵彻深度算法，其优点是不受靶体材料参数等条件的限制，在侵彻过程中根据预先装订在引信中的数据库信息，并结合高g值加速度传感器实测侵彻加速度，实时计算侵彻深度，能实现自适应炸点控制。

［1］Heuze F E．An Ovevriew of Projeetile Penetration into Geologic Materils，with Emphasis on Roeks［J］．Int J RoekMech Min Sci．，1990，27（2）．

［2］尹放林，严少华．弹体侵彻深度计算公式对比研究［J］．爆炸与冲击，2000，20（1）．

［3］Young C W．The development of empirical equation for the perdieting depth of an earth penetrating porject［M］．Snadia National Laboratories：Albuquerque，NM，1967．

［4］Young C W．Penetration Equations［R］．SNL：UAS，SAND97-2426／UC-705，1997．

［5］Department of the Army Fundamentals of portective Design for Conventional weapons．Technical Manual［R］．TM5285521，1986．

［6］王儒策，赵国志．弹丸终点效应［M］：北京：北京理工大学出版社，1993：19-28．

［7］徐建军，李世中．弹丸侵彻多层介质目标的动力分析［J］．弹箭与制导学报，1999：114-125．

［8］屈新芬，商顺昌，杨晴．影响弹丸侵彻性能的因素分析及引信方案探讨［J］．信息与电子工程，2003，1（3）．

［9］杨明，杨志刚，林祖森．加速度计输出信号的信息组成［J］．华北工学院学报，2000，21（1）．

［10］马游春．高冲击存储测试系统［D］．太原：华北工学院硕士学位论文，2003：75-88．