基于有限元法计算机直接制版设备辊筒模态分析

胡志炜

（柯达电子（上海）有限公司，上海 201206）

0 引言

采用CTP（compute to plate）直接制版［1］技术可以减少“印前拼版、晒版、拷贝等比较复杂工序”，不但提高了印刷的效率和速度，而且实现了数字页面向印版的直接转换，整个印前过程实现数字化，并逐渐渗透至各种印刷行业［2］。据“报协印刷工作委员会于2011 年度对中国报业印刷总印量统计中，共有139 家报业提供了有效数据，在这139 家报业印刷厂中，配有CTP 设备的已达116 家，CTP总制版量约为918 万张［3］”。从这些数据中已看出CTP 设备在国内已遍地开花。报业印刷最大特点就是出版速度快，讲究时效性。因此提高CTP 设备的出版速度已是箭在弦上，哪家公司开发的CTP 设备速度快、质量高，已成为了当前CTP 设备销售的竞争条件。

CTP 制版质量的控制一直是各厂家关注的问题，其中成像辊筒就是控制CTP 制版质量的核心机构之一。辊筒在旋转过程中任一质点均会产生离心力，继而形成惯性力系；又因为需要基于实际制版需求，辊筒的质量分布不均匀而致使辊筒各质点在旋转过程中产生的惯性力无法相互抵消；从而导致辊筒表面的应力分布不均匀，表面将产生一定的变形，表面的微小变形都会影响成像质量。再加上轴承的高速旋转也会带来微小振动，而这些轻微振动将造成成像质量的下滑。因为辊筒表面及版材发生变形，成像光点位置超过焦深范围，不能准确聚焦到版材表面的感光层上，产生模糊光点。除了成像质量问题以外，对辊筒进行动力学［4］分析可以找出辊筒的固有频率，计算出辊筒的N阶临界转速，从设计角度保证成像质量，杜绝失稳现象，避免共振产生，同时降低高转速产生的噪声。因此对辊筒的振动分析尤其重要。提高出版速度，就不得不加大激光头功率和辊筒的转速。从公司利益的角度来看，针对辊筒高转速动力学分析是非常有必要的。

1 有限元法动力学理论和临界转速的确定

利用有限元法进行辊筒动力学分析，需先分析单元特性，其目的是分析单元节点力、位移、速度和加速度之间的联系。然后通过局部坐标系变换为整体坐标系，对结构进行整体分析，建立整个结构点平衡方程组。

设单元的位移函数为de=Nδe，其中de表示单位位移函数向量，N 表示形函数矩阵，δe表示单元节点位移向量，其中de和δe都是关于时间的函数。将式de=Nδe对时间一阶求导，可以得出单位内任意点的速度（de）′＝N（δe）′。将式de=Nδe对时间二阶求导，可以得出单位内任意点的加速度为（de）″＝N（δe）″。根据达朗贝原理，“对于任意物理系统，所有惯性力或施加的外力，经过符合约束条件的虚位移，所作的虚功的总合等于零”［5］。因此可以得出在辊筒旋转时，将其惯性力Fem 施加在单元上，则单元处于动平衡状态，因此可以将其转化为静态问题。单元内任一点作用的单位体积的惯性力可以表示成

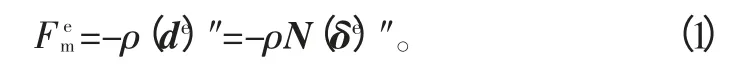
式中，ρ 表示单元质量密度，负号表示该点惯性力的方向与加速度方向相反。

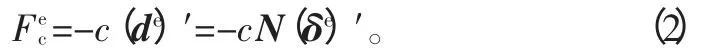
其中，c 是阻尼系数，单位速度下单位体积上的阻尼力，负号表示该点的阻尼力与速度方向相反。

由于单元在受力情况下发生了虚位移Δde=NΔδe，其中Δde表示单元虚位移，Δδe表示结点虚位移。根据虚功原理可以得出

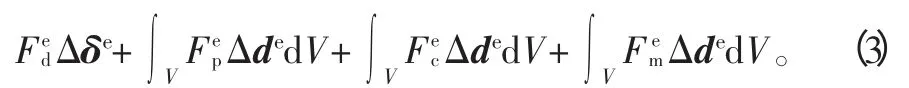
将式（1）、式（2）代入式（3）得外力虚功：

内力虚功为∫VσeεedV，因为外力虚功等于内力虚功，可求得：

公式两端左乘（NΔδe）-1和右乘（NΔδe）-1，同时因为在节点处的形函数矩阵为单位阵，且NΔδe是正交矩阵（正交坐标系），因此可以得出：

等式两边同时去掉Δ（δe）T，且由于δe、（δe）′、（δe）″和坐标无关。因此式（6）可写为

根据式（7）可知节点上的作用力共分为两类，一是作用于节点上的外载荷，另一个是相关单元对该节点的作用力，节点在这些力的作用下处于动平衡状态。可以将式写成通用动力学方程式F＝Kδ＋Cδ′＋Mδ″，式中：F为结构的整体载荷向量，是关于时间的函数；K为结构的整体刚度矩阵；C为结构的整体阻尼矩阵；M为结构的整体质量矩阵；δ为结构的节点位移向量矩阵；δ′为结构的节点速度向量矩阵；δ″为节点加速度向量矩阵；

单元质量阵、刚度阵、阻尼阵建立后，并根据坐标变换后组成总质量阵、总刚度阵和总阻尼阵。然后对边界条件进行支承条件处理。划分单元时，最好使支承点与节点重合，以得到较为精确解。支承若为刚性支承，则该节点的线位移和角位移均为0，若为弹性支承，并已知弹性支承的刚度系数为Kc，则应在总刚度矩阵［K］中，相对应于此支承处的对角元素上加上Kc即可。有时还需要考虑到轴承刚度Kb、轴承支座Ks以及基础刚度（除了以上刚度外的所有刚度，比如机架底座等）Kg，则此组合系统刚度Kc为

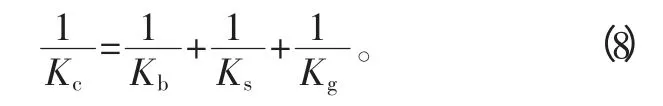
辊筒的临界转速即为辊筒的横向振动固有频率，根据转子的通用动力方程式F＝Kδ＋Cδ′＋Mδ″及标准模态解［6-7］的形式x=Xeiωt，其中当F、C 均为0 时，对应固有频率ω 和相应的模态向量X，可得出

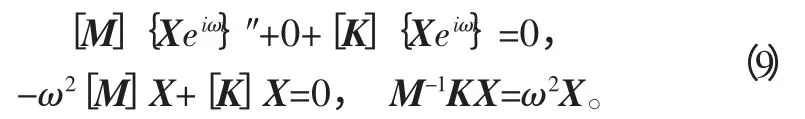
固有频率即为M-1K 的特征值的平方根。若考虑阻尼，则C 不为0，但F 需为0，就可以得出考虑刚度和阻尼情况下，辊筒真实的固有频率和临界转速。

2 辊筒动态特性分析

辊筒在旋转过程中形成固定振源，不同的角速度将对应不同的频率和振型。当振源频率接近辊筒旋转的固有频率时，将产生共振现场。共振时激光头无法在版材上进行有效的聚焦，版材上将出现白线、抖动、画面失真、鬼影等现象，对印版质量产生严重影响。因此研究辊筒的固有特性和振型将有利于在设计中避免共振问题的发生。

由于轴承座、滚动轴承及滚动轴承中的油膜都是弹性体，刚度不可能无穷大，支承刚度的不同将导致辊筒的变形量、临界转速和振型都会发生变化。且支承刚度越小，临界转速就越低。同时辊筒在转动过程中，轴承内部的摩擦阻尼和油膜阻尼也会对辊筒产生一定的影响。因此辊筒的模态分析需要考虑轴承的刚度和阻尼，分析其结构振动，求出结构固有频率和振型。分析辊筒结构特征首先需要建立有限元分析模型，通过有限数目单元，建立数学方程分别计算各个单元的受力和变形状况，最后汇总成整个有限元模型的应力和位移分布云图，并可通过模态提取方法—分块兰索斯法Block Lanczos 求出辊筒的N阶极限转速和相对应的振型。

由于辊筒的结构比较复杂，在Ansys 中建模比在专业的三维制图软件如Pro/E、SolidWorks、UG 和Ideas 较为困难。因此采用专业的三维软件可以弥补Ansys 在建模方面的不足。本文采用在SolidWorks 中建模，如图1 所示。然后将模型保存成Parasolid 的X_T格式，完整地导入到Ansys 中，最后完成所需的有限元分析。组件在导入前需在SolidWorks中检测是否有装配干涉，否则在Ansys 中容易造成无法对装配干涉件进行网格划分。Ansys Workbench 会自动扫描，建立接触，然后只需设置接触对就可以了。

模型在从SolidWorks 转换到Ansys Workbench 中为了保证尺寸一致，需要设定单位。定义mm为长度单位，kg为质量单位，N为力单位，s为时间单位。辊筒长度为1 708 mm、直径为459.2 mm，轴承采用的是NSK 生产的深沟球轴承，型号为6208，其宽度为18 mm、内径为40 mm、外径为80 mm。辊筒缸体和左右端盖均采用铝合金6061-T6 材料，其弹性模量为软件默认的7.1×104MPa，密度也是默认的2.77×103kg/m3，泊松比为0.33。轴承材料为高碳铬轴承钢，弹性模量采用2.0×105MPa，密度采用7.85×103kg/m3，泊松比采用0.3。然后通过Ansys Workbench 对左右端盖、辊筒缸体及轴承进行材料分配。材料分配完毕后，需要对端盖和缸体设置连接方式。由于端盖和缸体之间没有滑动，因此采用bond 的模式。为了简化阻尼模型，因此将摩擦阻尼和油膜阻尼认为是只具备摩擦系数的阻尼模型。外圈和滚珠之间、滚珠和内圈之间及保持架和滚珠之间均采用摩擦连接模式，摩擦系数为0.002，如图2所示。随后需对辊筒进行网格划分。由于缸体特征较多且较复杂，采用混合网格进行划分可在几何模型上，根据各部位的特点，分别采用自由、映射、扫略等多种网格划分方式，形成综合效果尽量好的有限元模型。网格节点数量达180 005 个，单元数量达98 596 个，如图3 所示。最后设置边界条件，由于辊筒旋转是轴承外圈转动，内圈固定不动。因此将内圈的位移设为零，保持架和外圈设为径向（Y 方向和Z 方向）自由，轴向（X 方向）位移为零，旋转自由度Y 方向和Z 方向均为零，X 方向自由，如图4 所示。完成所有设置后，进行模态分析。

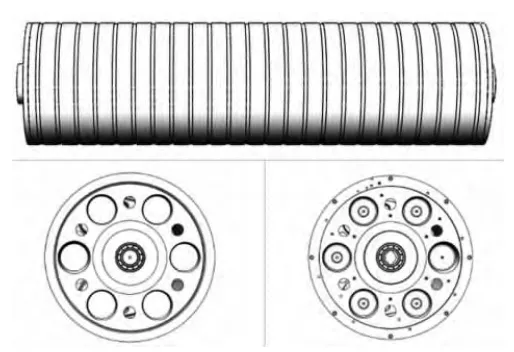
图1 辊筒和轴承动力学模型

图2 接触方式设置

图3 辊筒和轴承组件的网格划分

图4 边界条件的设定

3 模态分析及运行结果

Ansys Workbench 根据有限元法动力学理论建立数学模型，经计算得到辊筒组件的固有频率及位移变化，通过缩放比例查看变形的位置。图5 和表1 显示的是辊筒前6阶模态振型和固有频率。由于没有限制绕X 轴的转动，因此第一阶振型是刚体运动的振型，其特点是辊筒表面的变形量一致，第二阶的振型转化为挠性体运动的振型。

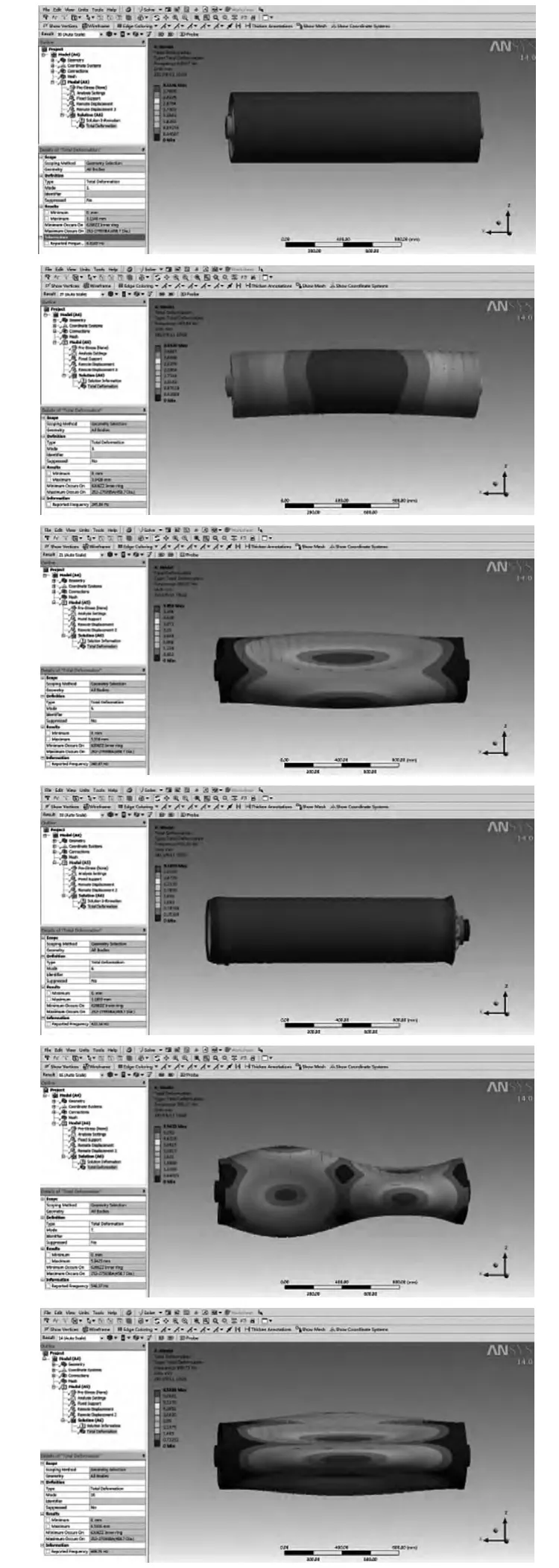
图5 辊筒组件前六阶模态振型

表1 前六阶辊筒固有频率和最大变形位移

4 辊筒静态分析

从辊筒的固有频率可以看出第二阶模态固有频率为245.84Hz，则其转速为245.84×60＝14 750.4 r/min，已经超出了轴承6208 的极限转速8500r/min。同时考虑到激光在版材上连续曝光的速度，及辊筒在旋转时的振动值不能超过20 μm，需对辊筒进行静态分析。分析结果中辊筒位移分布云图如图6 所示，应力分布云图如图7 所示。从分析的结果可知辊筒振动在不超过20 μm 时的最大转速为891.02 r/min。其对应的最大应力值为2.367 9 MPa 远小于辊筒材料铝合金6061-T6 的屈服强度55.2 MPa。目前此辊筒已用在柯达CTP 设备中，考虑到零部件的加工制造误差，将实际的工作转速设定为500 r/min。

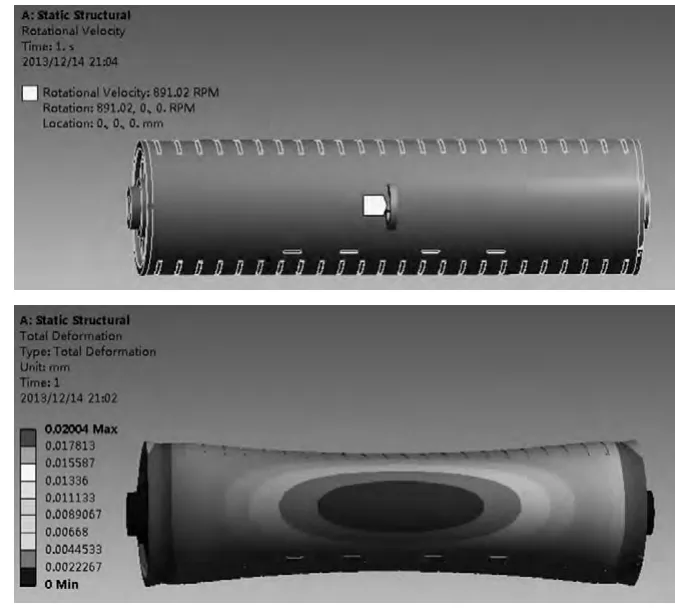
图6 辊筒位移分布云图

图7 辊筒应力分布云图

5 结论

通过对成像辊筒模态分析，利用SolidWorks 建立有限元模型，并导入至Ansys Workbench 中进行模态分析，得到辊筒前六阶临界转速和振型。其中第一阶振型为刚性模态，第二阶振型转化为挠性模态，虽然轴承所能承受的最大转速低于二阶临界转速，但远高于在满足成像质量前提下的891.02 r/min 转速，辊筒不会产生共振现象。在对成像辊筒进行静态分析，可得到辊筒承受的最大应力低于材料的屈服强度，满足制版设备的功能要求。

［1］Chung R.Test Targets 9.0 School of Print Media［M］.Rochester Institute of Technology，2009：2-19.

［2］赵伟建，章学良，李合成.浅谈CTP 的实际运用［J］.印刷杂志，2004，218（5）：14-16.

［3］张梦童.2011 中国报业CTP 的跨越式成长——2011 年中国报业CTP 制版量调查解析［J］.印刷杂志2012（11）：10-11.

［4］Kiral Z,Karagulle H.Vibration analysis of rolling element bearings with various defects under the action of an unbalanced force［J］.Mechanical Systems and Signal Processing，2006（20）：1968-1973.

［5］丁科，陈月顺.有限单元法［M］.北京：北京大学出版社，2007：114-116.

［6］凯利S M.机械振动［M］.北京：科学出版社，2002：99.

［7］马淑梅，柯于林，李爱平，等.基于ANSYS 的高效永磁同步电机主轴静动态特性有限元分析［J］.机械设计，2013，30（2）：83.