基于萤火虫算法的学习遗忘效应BFSP问题研究

赵 静， 叶春明

（上海理工大学 管理学院，上海 200093）

具有学习遗忘效应的生产调度优化问题是目前工业界和工业工程学术界都关注的前沿性研究领域.流水车间调度问题是经典生产调度问题中研究最为广泛的一类调度问题，是许多实际生产调度过程的简化模型.其中，阻塞流水车间调度问题（blocking flow shop scheduling problem，BFSP）是流水车间调度问题的一个重要分支，具有较高的理论研究价值.目前，机器数包含2台以上的阻塞流水车间调度问题已被证明为NP 难题［1］，再进一步考虑学习遗忘效应，优化求解更加困难.因此，研究具有学习遗忘效应的BFSP调度问题更具有重要的理论研究意义和实践应用价值.本文采用的萤火虫算法［2］是由剑桥学者Yang于2008年提出的一种模拟自然界中萤火虫发光行为的仿生智能算法，具有模型简单、收敛速度快等特点.

在经典的排序理论中，工件的加工时间通常被假设为固定的常数.然而在许多实际生产过程中，由于机器或工人反复连续加工相同或类似的工件，他们的操作会越来越熟练，学习效应会使得工件的加工时间缩短.同时，工件种类的变化或生产中断等现象，引起学习效果的减弱，遗忘效应会造成工件的加工时间延长.关于生产过程中学习效应的研究始于20世纪30年代，美国康奈尔大学的Wright博士在研究飞机制造业的生产效率时发现，单位生产成本随着产量的增加而降低，进而提出80%假设，即产量增加一倍，单位成本会降低20%［3］.有关生产时间或者成本的学习效应理论在提出后不久就得到了实际应用，但直到1999年Biskup［4］才首次描述了加工工件具有学习效应的单机排序问题，提出了一种与加工位置有关的学习效应模型.Kuo等［5］认为工件的加工时间可能与已经加工完的工件的加工时间有关，提出了一类与时间相关的学习效应模型.张新功等［6］提出指数学习效应和位置学习效应同时发生的新的排序模型，并给出求解单机排序情形以及流水机排序某些特殊情形下的多项式时间算法.杨明明［7］研究了具有Dejong学习效应和遗忘效应的间歇批生产的单机排序问题，其学习效应模型仅与加工位置有关.王桂娜等［8］以成组生产的单机系统为研究对象，提出了一种新的考虑学习遗忘效应的成组调度模型，并通过算例分析验证了模型的有效性.

在以往考虑学习效应的生产调度研究中，学习效应模型较为单一，遗忘效应也容易被忽略，且大多数学习模型的应用局限于单机环境.即使是流水车间作业环境，一些学者也仅通过近似算法，如多项式时间算法，对某些特殊情形进行了验证.现有文献关于具有学习效应和遗忘效应的流水车间调度问题的研究仍较少，且由于优化算法求解规模的有限性和求解质量的不足，应用领域局限于经典生产调度问题的简化模型，与实际生产问题的结合仍有待加强.本文在机器数量方面尝试突破，研究小批量生产时的阻塞流水车间调度问题，同时考虑学习效应和遗忘效应.本文参考王桂娜等提出的学习遗忘效应的整合调度模型，采用结合基于Pairwise局部搜索策略［9］的萤火虫算法，通过对Car类问题的仿真测试验证了算法的可行性和有效性，并证明了学习效应和遗忘效应现象在实际生产过程中不可忽略的影响.

1 问题描述

阻塞流水车间调度问题考虑n个工件在m 台机器上的加工过程.该调度问题需满足如下约束：每个工件都有m 道工序，均依次在机器1至机器m 上进行加工；每个工件在每台机器上最多只能加工一次；在某一时刻，每台机器一次最多同时加工一个工件；每台机器上各工件的加工顺序相同；一个工件在完成某道工序后，在下游机器变为可用之前将滞留在当前机器上.

在本文中，令π＝｛π1，π2，…，πn｝表示所有工件的一个调度排序；pi，k表示工件i（i＝1，2，…，n）在机器k（k＝1，2，…，m）上的实际加工时间，即已考虑学习遗忘效应的加工时间；di，k表示第i个工件在第k台机器上的离开时间.具体计算公式为

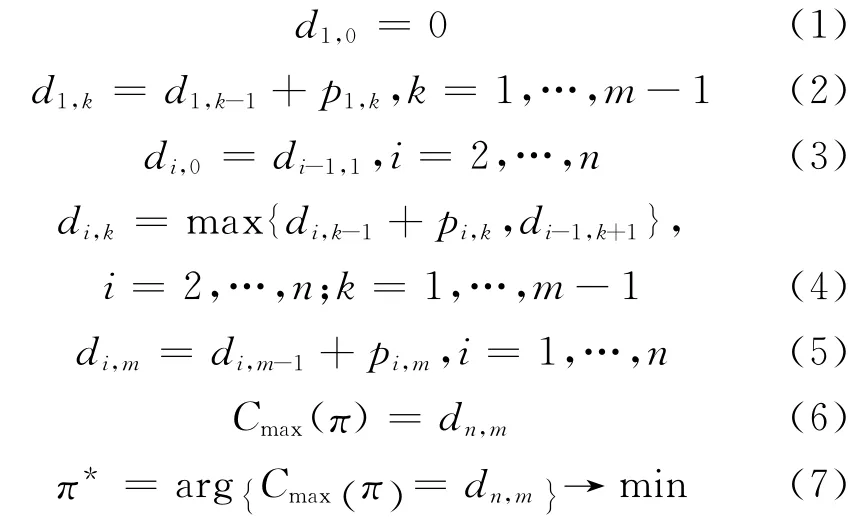
其中，式（6）即为最大完工时间，式（7）表示最小化最大完工时间所对应的调度排序方案.

2 学习遗忘效应的调度模型构建

考虑对阻塞流水车间调度问题中的工件进行小批量生产，同种工件称为1个工件组.在生产1个工件组内的同种工件时，由于反复加工相同的工件，使得加工顺序中排在后面加工的工件的加工时间缩短，即学习效应对加工时间的影响；当机器从加工一种工件组转换到另一种工件组时，学习效果会相应减弱，即存在遗忘效应.造成遗忘效应的因素有很多，例如生产设置时间、工件转换以及预防维护时间等，本文考虑的影响因素为不同工件之间的转换.遗忘率η表示为

式中，η表示不同工件组间的遗忘率；φ 表示遗忘参数；θj－1，j表 示 工 件 组Jj－1和 工 件 组Jj之 间 的 相 似度，取值范围为［0，1］，各工件组之间的相似度构成一个对角线为0的对称矩阵.

小批量生产的生产方式中存在不同的学习模式，本文考虑两种学习效应：加工同一种工件时的学习效应；不同工件组间的学习遗忘效应.

a.加工同一种工件时的学习效应.此时的学习效应主要取决于工件加工的次数，即其对应的加工位置.本文基于Biskup 与加工位置有关的学习模型，提出Pjλ＝Pj1λa.其中Pj1表示加工工件组Jj中第一个工件的实际加工时间，若j＝1，P11即工件组J1的基本加工时间；Pjλ为工件组Jj中第λ个工件的实际加工时间；a≤0为常数，表示学习因子.

b.不同工件组间的学习遗忘效应.由于加工工件的种类不同，存在遗忘效应，计算工件的实际加工时间时，需考虑遗忘效应产生的影响.因此，与加工位置有关的学习模型已不能准确求解此时工件的实际加工时间.本文的学习遗忘模型参考王桂娜等［8］提出的学习遗忘模型，工件的实际加工时间可分为两部分：学习效应引起的工件实际加工时间的缩短，表示为前一个工件的实际加工时间与其基本加工时间的比值；遗忘效应引起的学习效果的减弱，表示为对累积学习效应的遗忘程度.因此，同时考虑学习效应及遗忘效应，加工工件组Jj的第一个工件的实际加工时间为

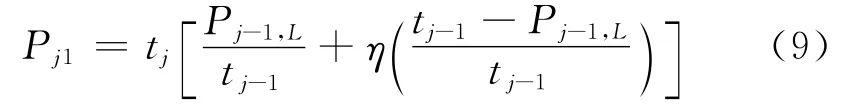
式中，tj为工件组Jj的基本加工时间；L 为批量，则Pj－1，L为工件组Jj－1中最后一个工件的实际加工时间为不考虑遗忘效应时的学习效应；为累积的学习效应；为对累积学习效应的遗忘程度，即遗忘效应.

本文考虑的生产模式为小批量生产，对某一工件进行小批量生产时，只需考虑学习效应.当该工件组生产结束，转换到下一工件组，此时需考虑遗忘效应的存在.通过式（9）求得工件组第一个工件的加工时间，然后工件组内各工件的加工时间只需考虑学习效应.

3 萤火虫算法求解学习遗忘效应阻塞流水车间调度问题

3.1 萤火虫算法

萤火虫算法是通过模拟自然界中萤火虫发光行为而构造出的一种随机优化算法.萤火虫算法舍弃了部分萤火虫发光行为的生物学特点，只保留以萤火虫发光特性为依据在搜索空间内寻找伙伴的特点，然后向邻域空间中位置较优的萤火虫移动，最终实现位置的优化［10］.

在萤火虫算法中，萤火虫之间相互吸引主要取决于两个因素，即其亮度和吸引度.亮度决定了萤火虫所在位置的优劣和移动方向，吸引度则决定了萤火虫移动的距离，通过不断更新萤火虫亮度和吸引度，实现目标的优化.萤火虫算法的数学描述如下［11－12］：

定义1 萤火虫的相对荧光亮度为

式中，I0表示萤火虫的最大荧光亮度，即自身（r＝0处）荧光亮度，与其对应的目标函数值有关，目标函数值越优则自身亮度越高；γ 表示光强吸收系数，萤火虫的荧光会随着距离的增加和传播介质的吸收而减弱，所以设置光强吸收系数来体现该种特性，可设为常数；ri′j′表示萤火虫i′与萤火虫j′之间的距离.

定义2 萤火虫的吸引度为

式中，β0为最大吸引度，即光源（r＝0处）吸引度；γ，ri′j′意义同上.

定义3 萤火虫i′被萤火虫j′吸引并向其移动的位置更新公式为

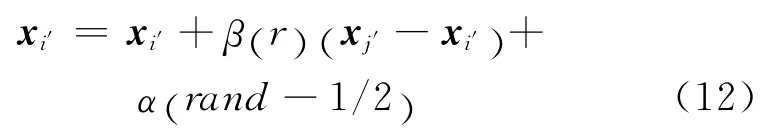
式中，xi′，xj′为萤火虫i′和萤火虫j′所处的空间位置；α为步长因子，是［0，1］上的常数；rand 为［0，1］上服从均匀分布的随机因子；扰动项α（rand－1／2）是为了避免过早陷入局部最优.

3.2 编码方式

由于萤火虫算法中所有萤火虫个体的位置都是连续值矢量，标准萤火虫算法无法实现工件排序的更新，因此应用萤火虫算法求解BFSP问题，首先要解决的问题就是采用合理的编码方式实现位置矢量到工件排序的映射.本文采用基于最小位置值规则的随机键编码方式［13］，将萤火虫个体的连续位置xi′＝［xi′，1，xi′，2，…，xi′，n］转 换 为 离 散 的 加 工 顺 序π＝（π1，π2，…，πn），从而求得萤火虫个体所对应的优化问题的目标值.

3.3 基于Pairwise的局部搜索

为了改善萤火虫算法的局部搜索能力，本文采用基于Pairwise的局部搜索算法.首先，将第一个位置的工件与它后续的工件依次进行交换，如果优化目标得到改善，则交换这两个工件的顺序，否则不进行交换；然后，依照同样的方法，对剩余的所有工件逐一进行成对交换操作.

3.4 算法流程

萤火虫算法求解基于学习遗忘效应的BFSP的具体流程如下：

a.初始化算法的基本参数，设置萤火虫数目为m，最大吸引度为β0，光强吸收系数为γ，步长因子为α，最大迭代次数为Tmax；

b.随机初始化萤火虫个体的位置，并计算每个个体的目标函数值作为各自的最大荧光亮度I0；

c.计算萤火虫个体的相对亮度I 和吸引度β，根据相对亮度决定萤火虫的移动方向，然后更新个体的空间位置，并重新计算相对亮度；

d.对种群个体进行基于Pairwise的局部搜索，并更新种群；

e.当算法达到最大迭代次数时则算法终止，输出最优目标函数值及对应的调度排序；否则，转至步骤c.

4 仿真测试及结果分析

实验仿真环境为：Windows 7操作系统，处理器主频2.0GHz，内存3.0GB，采用Matlab R2009b编译软件.算法参数设置为：萤火虫数目m＝30，最大吸引度β0＝1.0，光强吸收系数γ＝1.0，步长因子α＝0.2，最大迭代次数Tmax＝100.

4.1 求解BFSP调度问题

采用著名的Car类测试问题进行实验仿真测试，包括8个测试实例.为验证算法的有效性，首先测试不考虑批量生产，且不存在学习遗忘效应情况下的阻塞流水车间调度问题.对每个实例均独立运行10次，迭代次数100次，测试结果如表1所示.图1为萤火虫算法求解Car1问题独立运行20次的收敛图.

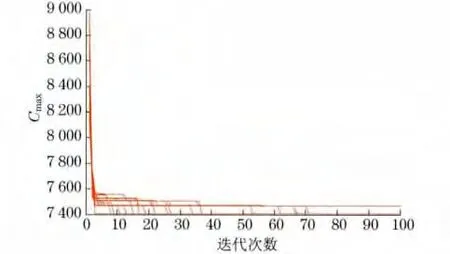
图1 求解Car1问题的收敛图Fig.1 Convergence figure of Car1

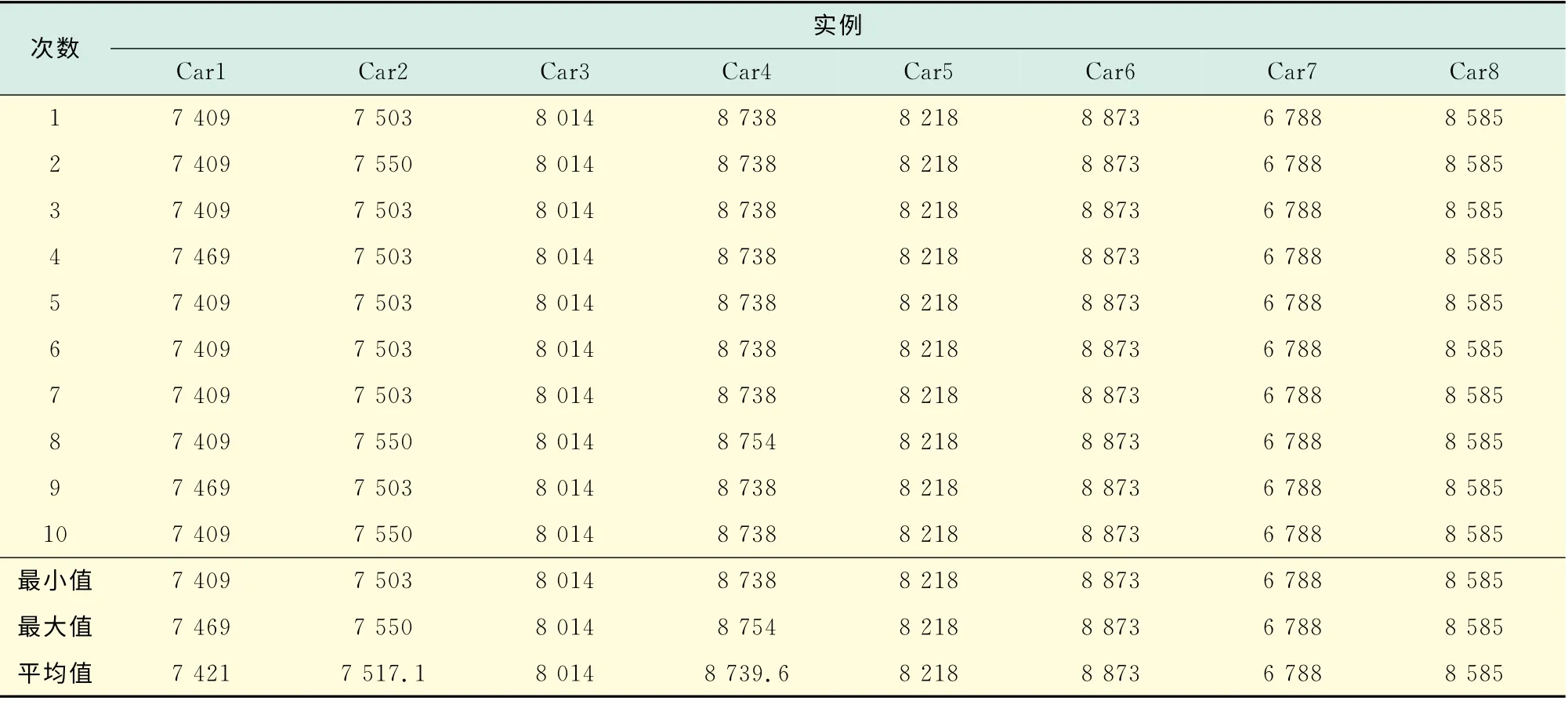
表1 Car类问题测试结果Tab.1 Test results of the Car kind problem

从表1的测试结果可以看出，以Car类测试实例为仿真数据，萤火虫算法均能搜索到最优解，说明该算法在求解阻塞流水车间调度问题中可行，而且寻优率较高.从图1可以看出算法的收敛速度较快，说明算法具有良好的全局收敛性能.

4.2 求解基于学习遗忘效应的BFSP调度问题

以Car1问题为仿真实例，对所有工件进行小批量生产，批量L 均为3，工件组间相似度矩阵为

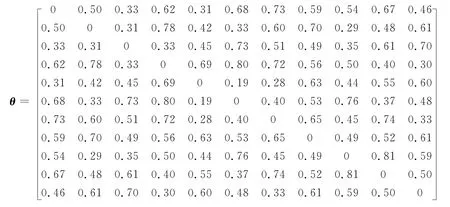
表2为不同学习因子、不同遗忘参数下Car1问题的寻优结果，用以讨论学习因子及遗忘参数对寻优结果的影响.图2（a）和（b）分别为学习效应对应80%的学习曲线，即学习因子为－0.322、遗忘参数分别为0.15，0.45、算法迭代100 次、独立运行20次所得结果.

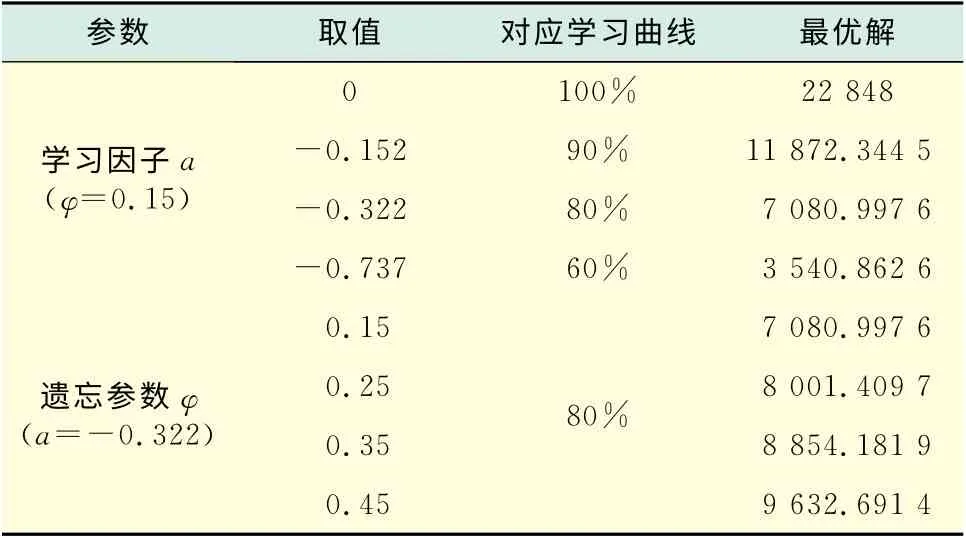
表2 学习因子及遗忘参数对寻优结果的影响Tab.2 Influences of learning factor and forgotten parameter on optimizationresults

由图2可以看出，萤火虫算法可以有效搜索到优化目标的满意解，具有较快的收敛速度和较好的全局搜索能力.由表2可以看出，学习因子a从0变化到－0.737时，即学习曲线从100%变化到60%，阻塞流水车间调度问题的最大完工时间大大缩短.即使采用90%的学习曲线，目标函数值相较不考虑学习效应时也缩短了将近50%.学习因子越小，完工时间也越小，即学习效应能够提高生产效率.同时可以发现，随着遗忘参数的增加，最优的最大完工时间也增大，这是因为较大的遗忘参数意味着较大的学习效果的退化.学习效应及遗忘效应现象在实际生产过程中是客观存在的，而且这种现象对实际生产调度的影响也是不可忽视的.

图2 具有学习遗忘效应Car1问题的收敛图Fig.2 Convergence figure of Car1with learning and forgetting effects

5 结束语

针对以最小化最大完工时间为优化目标的阻塞流水车间调度问题，同时考虑学习效应及遗忘效应对生产调度的影响，构建了该问题的学习遗忘调度模型，并采用改进的萤火虫算法进行求解.在求解过程中，结合基于Pairwise的局部搜索算法，改善了萤火虫算法的寻优能力.通过对经典的Car类问题进行大量仿真测试，结果表明了改进萤火虫算法求解阻塞流水车间调度问题的可行性和有效性.同时，对Car1问题的学习遗忘调度模型进行求解，通过对比不同学习因子、不同遗忘参数下的测试结果，发现随着学习因子的降低，最大完工时间也逐渐减小，则学习效应能够缩短完工时间，提高生产效率；而随着遗忘参数的增加，最大完工时间也逐渐增加，则遗忘效应会减弱学习效果，导致完工时间延长.实际生产调度中存在的学习效应和遗忘效应是非常复杂的，本文只对其作了初步研究，还存在很多不足，作为下一步研究方向，仍需展开大量研究工作.

［1］Hall N G，Sriskandarajah C.A survey of machine scheduling problems with blocking and no－wait in process［J］.Operations Research，1996，44（3）：510－525.

［2］Yang X S.Nature－inspired metaheuristic algorithm［M］.Bristol：Luniver Press，2008.

［3］Wright T P.Factors affecting the cost of airplanes［J］.Journal of the Aeronautical Sciences，1936，3（4）：122－128.

［4］Biskup D.Single－machine scheduling with learning considerations［J］.European Journal of Operational Research，1999，115（1）：173－178.

［5］Kuo W H，Yang D L.Minimizing the total completion time in a single－machine scheduling problem with a time－dependent learning effect［J］.European Journal of Operational Research，2006，174（2）：1184－1190.

［6］张新功，严广乐，唐国春，等.具有指数和位置学习效应的机器排序问题［J］.运筹与管理，2011，20（2）：97－101.

［7］杨明明.具有学习效应和遗忘效应的间歇批生产的单机排序问题［J］.枣庄学院学报，2010，27（5）：39－44.

［8］王桂娜，俞秉昊，潘尔顺.成组生产下的考虑学习和遗忘效应的调度策略［J］.工业工程与管理，2012，17（5）：60－64.

［9］王凌，刘波.微粒群优化与调度算法［M］.北京：清华大学出版社，2008.

［10］刘长平，叶春明.一种新颖的仿生群智能优化算法：萤火虫算 法［J］.计 算 机 应 用 研 究，2011，28（9）：3295－3297.

［11］Yang X S，Deb S.Eagle strategy using lévy walk and firefly algorithms for stochastic optimization［J］.Studies in Computational Intelligence，2010，284：101－111.

［12］Yang X S.Firefly algorithms for multimodal optimization［C］∥Proceedings of the 5th International Symposium.Heidelberg：Springer Berlin Heidelberg，2009.

［13］刘长平，叶春明.求解置换流水车间调度问题的布谷鸟算法［J］.上海理工大学学报，2013，35（1）：17－20.