数学教学知识评价工具评介及启示*

陈碧芬， 张维忠

（浙江师范大学教师教育学院，浙江金华 321004）

学科教学知识(PCK)是由舒尔曼(Lee S.Shulman)提出的，它指的是教师在面对特定的学科主题或问题时，如何针对学生的不同兴趣与能力，将学科知识组织、调整与呈现，实行有效教学的知识。［1］这是一种使教师与学科专家有所区别的专门知识，是教师专业知识的核心成分和教师专业化的重要标志。［2］PCK具有个体性、缄默性、情境性、动态生成性等特点，而数学教师的PCK被称为数学教学知识(MPCK)，因此MPCK也具有与一般PCK同样的特点。MPCK虽然有公共知识，但由于其主要是教师个人教学建构的结果，［3］因此更多地认为它是个体知识，即具有个体性及动态生成性。又由于MPCK不是外显于个体的，因此它是缄默的。再由于教师的PCK与特定的主题相联系，某教师在某一主题或问题上拥有丰富的、良好的MPCK，但是并不表示此教师在其它课题上的MPCK也表现良好。因此，在众多的关于MPCK的研究中，其评价问题一直是一个难点。本文旨在介绍几种MPCK的评价工具，以期对我国数学教师MPCK评价有所启示。

一、MPCK评价工具评介

MPCK的评价从总体上看，主要采用试题(问卷)、课堂观察、访谈等工具。但是，由于目的不同，在评价工具的使用上也有不同侧重。下面以美国康乃狄克州基础教育教师资格考试中采用的PCK评价工具、数学教师教育与发展研究(TEDM)采用的MPCK评价工具及运用德尔菲(Delphi)法设计的MPCK评价工具为例，介绍几种常见的MPCK评价工具。

(一)美国康乃狄克州基础教育教师资格考试中采用的PCK评价工具［3］

20世纪80年代末90年代初，美国康乃狄克州实施了基础教育教师资格考试。这是康乃狄克州教师评估体系中三个层次中的一个。其中，第一个层次是基本技能考试;第二个层次是完成大学本科学位及参加一个教师教育项目;第三个层次是教学第一年进行的各种评价，包括观察及工作评价，也包括PCK评价。由于考试人数众多，因此采用纸笔考试及多项选择题来评价这些教师的PCK。

此考试机构认为适合评估教师PCK的题目应是以下几种:(1)给一个课时计划，被测者必须给出此计划的最理想的补充内容或者最适合此课题的行为目标;(2)给四个工作单或者学生学习活动的描述，被测者必须给出当前工作单或者活动接下来最合适的情形，或者最切合具体目标的工作单或活动;(3)给一个已经完成的工作单或者已经完成的学生工作，被测者必须给出此学生工作最合适的评价，或者提供给学生最合适的反馈、解释或者补救活动;(4)给出一个学生学习活动的描述，被测者必须给出学生完成此活动所需的技能，或者对此活动最有用的技能;(5)给出一节课的教学目的，被测者必须选择最适合此课题教学的资源。

通过这些题目选拔了一批数学教师。但是，后来发现被选拔出来的教师的教学效果不一定好，而有一些在测试中取得较差成绩的教师的教学效果比有些成绩好的教师还要好。分析这些现象，原因可能有以下几点:一是有些教师不善于表达，而有些教师善于表达;二是有些教师在答题时较为认真，而有些教师却不够认真;三是静态的测试题不能完全反映教师头脑中“鲜活”的MPCK，这也被认为是最主要的一点。

(二)TEDS-M中采用的MPCK评价工具［4］

国际教育成就评价协会(IEA)从20世纪开始，组织了多次关于数学教育成就的国际比较研究，研究发现:一些发达国家的学生的成绩不如包括中国在内的儒家文化圈下的国家的学生。这引起了数学教育研究者尤其是西方学者的思考。他们从课程、课堂教学等方面寻找原因，其中数学教师的专业知识的比较研究也是一个重要方面。为了考察不同国家是如何培养中小学数学教师的，此协会发起并组织了一项关于中小学数学教师教育的国际比较研究——“数学教师教育与发展研究”(TEDS-M)。这项研究主要考察未来教师“为了教学的数学知识”(MKT)与MPCK。

为了能够体现研究的科学性与客观性，TEDSM研究人员在“21世纪数学教学”(MT21)项目研究的基础上借鉴“以德国人为本的COACTIV研究”成果，最终制定了MPCK评价框架和评价工具。此评价框架由三个指标构成，即数学课程知识、数学教学计划知识和数学教学实施知识。每个指标下又有若干子指标构成，具体如下:

指标1:数学课程知识。其中又分为以下5个子指标:(1)知道数学课程;(2)确立合适的学习目标;(3)明确学习过程中的关键点;(4)选择达到学习目标的可能路径并且知道课程之间的内在联系;(5)知道不同的评价目的和形式。

指标2:数学教学计划知识。其中又分为以下6个子指标:(1)选择恰当的活动;(2)预设典型的学生反应，包括困难或误解;(3)设计合适的方法呈现数学内容;(4)联系教学方法和教学过程;(5)明确解决数学问题的不同方法;(6)选择合适的评价形式。

指标3:数学教学实施知识。其中又分为以下6个子指标:(1)解释或表征数学知识;(2)诊断学生的反应，包括困难或误解;(3)分析或评价学生的数学学习;(4)分析学生问题的内容;(5)对预料之外的教学情况作出反应;(6)提供合适的反馈。

TEDS-M根据此评价框架开发了试题库、测试模块和测试手册，测试题型包括多项选择题、复杂多项选择题和问答题三类。同时，由于MPCK是数学教师对特定主题如何进行有效教学的知识，因此TEDS-M还根据“数与运算”、“几何与测量”、“代数与方程”以及“数据与概率”等不同的知识维度对MPCK进行内容细化并编制了相应的测试题。为了保证在只有60分钟的测试时间内能覆盖评价框架中的所有内容，TED-M应用项目反应理论，在测试手册中采用了轮换模块设计。同时，为了便于比较，采用了基于项目反应理论的尺度分数来展示测试结果，并且界定了尺度上的锚点。

但是，这种试题测试不能完全检测出未来教师MPCK，有很多学者采用了与其他方法相结合的方式来反映教师MPCK。如Shuhua An，Gerald Kulm ＆ Zhonghe Wu，Alexandra Corleis， Björn Schwarz＆Gabriele Kaiser等人分别对中美、中德数学教师MPCK进行比较，除了采用或改编TEDM的试题外，还结合课堂观察、访谈等方法收集数据，能较好地反映出教师 MPCK。［5-6］

(三)运用Delphi法设计的MPCK评价工具

课堂观察、访谈等作为评价教师MPCK采用的一般手段，可以深入地了解教师MPCK。但这是一件很费时费力的事情，如何才能找到一个有效的工具呢?

Agida Gabil Manizade＆ Marguerite M.Mason认为可以运用Delphi法来设计评价MPCK的工具。他们以中学中几何、测量、分解与重组图形为例，选取数学或数学教育研究专家、数学教育专家、数学教师及数学教育管理人员各5名，解释如何采用Delphi法设计测量教师MPCK的工具。［7］

首先，他们认为MPCK应该包含以下知识:关于有效表征及合适教学技巧的知识;关于某一特定知识困难和误解的知识;关于学生发展水平和能力的知识;关于数学观念的知识。

其次，采用Delphi法设置评价MPCK的工具。Delphi法采用的步骤是:

第一步，将初步的调查问卷发给研究对象，请他们做以下几件事情:(1)浏览所有题目;(2)对其中的一些题目进行修改;(3)对每个题目的效度进行打分，分值范围为1-5分(1表示设计得最差;5表示设计得最好);(4)列出其他的评价或问题;(5)将问卷以邮件、传真或寄信的方式返还。

第二步，将所有意见和建议汇总后，还要做以下几件事情:(1)浏览所有的评价和打分;(2)浏览所有修改过的题目;(3)列出建议修改的地方;(4)列出其他的评价或问题;(5)返回问卷给研究对象。

第三步，重复第一、二步骤，直到达成一致意见。

最后，形成测试MPCK的试题。

比如，Agida Gabil Manizade＆ Marguerite M.Mason请20名愿意参加研究的专家(5名几何教育研究专家、5名中小学教育专家、5名超过20年教龄的教师及5名数学教育管理人员)对测试教师在几何与测量这一主题上的MPCK进行评价和修改。经过以上步骤，修改后用于测试MPCK的题目其信度与效度都有所提高。例如，以下是研究者设计的评价教师MPCK试题中的第五题:

Wilson老师要求她七年级的学生比较下图中表示的三角形与平行四边形的面积。他们的高是一样的。

有两个组的学生得出了正确答案，即它们的面积是一样的。但是他们的解释是不同的。

第一组用以下的图示来解释:

第二组用以下的图示来解释:

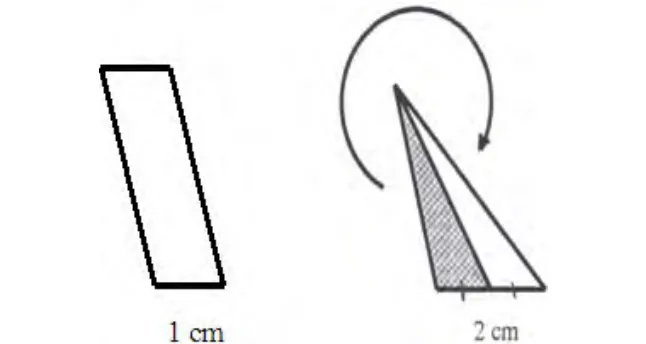
哪个组的学生的思维水平高?请说明理由。

哪个组的学生存在数学误解?如果有，是什么数学误解导致了学生的错误答案?如果没有，请比较两种解答方法。如果你是中学教师，当你的学生出现了以上两种解释时，你会怎么做?会采取怎样的教学策略?

然后分别把试题寄给专家组的各个成员进行审核。专家组从问题的清晰度和合理性、表述的简洁性、准确性与逻辑性等角度提出了意见和建议，最终形成了如下所示的问题:

Wilson老师要求她七年级的学生比较下图中表示的平行四边形与三角形的面积。他们的高是一样的。

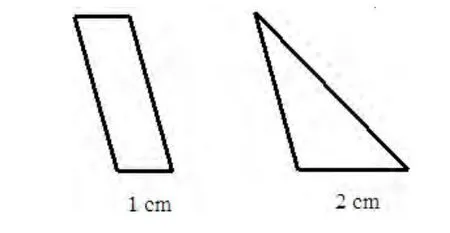
有两个组的学生得出了正确答案，即它们的面积是一样的。但是他们的解释是不同的。这两个组分别用以下图示来解释他们的答案:

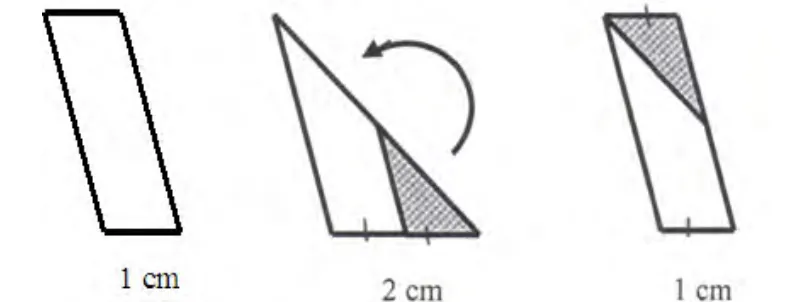
第一组的解答

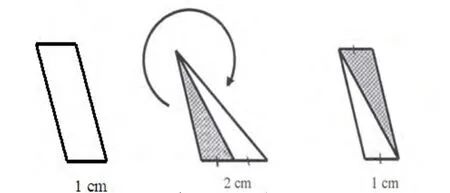
第二组的解答

(a)学生在正确解答此题时可能用到哪些重要的数学观念?

(b)Wilson老师不能确定这两种解释都是对的。你怎么看?为什么?

(c)哪个组的学生存在数学误解?如果有，是什么数学误解导致了学生的错误答案?如果没有，这两个组的思维有何不同?

(d)接下来你会采取怎样的教学策略和(或)任务?为什么?

但是设计这样的MPCK评价工具，首先需要一个专家组愿意并认真评价这些试题，且能认真提出修改意见和建议。

二、对研制合理、科学的MPCK评价工具的启示

由于PCK的个体性、缄默性、情境性及动态生成性等特点，决定了评价PCK是一个难点问题。从以上几种评价工具制定的介绍，我们发现各种工具都有自己的优缺点，难以找到能准确反映教师MPCK的特定工具。但是，从这些评价工具的产生及应用中，我们可以得到以下启示。

(一)针对不同的需要选用适合的工具

不管是美国康乃狄克州基础教育教师资格考试，还是TED-M中对未来教师MPCK的检测，以及运用Delphi法设计的PCK评价工具，都在追求用适合的、足够多的试题来评价教师MPCK。但是，这些试题都不能完全反映出教师MPCK，从而产生了课堂观察、访谈等工具来辅助甚至代替。但是，这些方法费时又费力，且涉及的教师相对比较少。我们认为，采用试题跟采用课堂观察、访谈这两种方法各有千秋，应根据不同的需要选择合适的工具。

若是想大面积地、粗略地了解教师MPCK，可以采用试题这一评价工具。例如，想要了解某一高等师范院校约320名数学专业师范生MPCK的整体现状，对每个师范生都进行课堂观察、访谈是不可能的。此时可以采用试题检查，但采用的试题必须经过严格的设计，比如Delphi法。采用这种方法，不仅进行了预测(向教师发问卷调查)，而且还向专业人士进行了咨询。从这个意义上说，这样研制的评价工具，其效度、信度都是较高的。

若是针对评价个人或者某个群体的教师专业发展，尤其是MPCK发展，采用试题就不是太恰当了。这时可以采用课堂观察、访谈等方法。这有多方面的原因:第一，访谈提纲中可以包含检测教师MPCK的试题内容，还可以根据教师的回答进行追问，能更深入地了解教师MPCK;第二，由于MPCK是缄默的，因此通过试题等方法，难以真正完全地反映出教师MPCK，而教师在课堂上的教学行为能较为真实地反映教师的MPCK。因此，通过课堂观察一方面可以验证在访谈中教师的回答有没有不实情况，另一方面可以发现前一次访谈中没有注意到的情况。这也就意味着访谈不应只做一次，课堂观察前后都应访谈。

然而，有些情况下，需要两种方法都采用。比如，教师招聘考试中需要检测应聘教师的MPCK，那么我们可以多种方法结合。首先，由于参加应聘的教师很多，可以先采用试题检测应试者的MPCK，选出较为优秀的应试者;然后，再通过课堂观察、访谈，深入了解，最终选择合适的教师。

(二)建立MPCK评价工具库的必要性

综观MPCK的研究发现，不同的研究者选择了教师在不同主题上的MPCK，较为零散和混乱。而且，这些研究也表明，是由一些教育研究者去评价教师MPCK，而没有教师自我评价MPCK。在中国教育专家不能满足需求的情况下，教师的专业发展主要还是靠自我反思。既然MPCK是使数学教学最有效的知识之一，那么在日常教学中教师反思自己的MPCK也很有必要。那么，如何反思?怎么才能发现自己关于某一主题MPCK的缺乏呢?如果能够提供一个教师MPCK的测试库，就能从一定程度上促进教师有效教学，促进其专业发展。

此库必须包含以下内容:(1)评价PCK的试题及课堂教学行为分析的要点;(2)试题的参考标准、课堂行为评价参考标准;(3)针对不同的问题或主题，给出相应的策略。需要说明的是，此处的参考标准并不是绝对标准，有时只是提供一些思考的方向;此处的策略也不是针对某一具体问题的具体策略，而是模糊策略，比如看相关的书籍、杂志等。

(三)MPCK评价工具的完善与发展是一个长期的过程

PCK在20世纪80年代提出来后，还没有一个完全有效的评价工具。由于社会的发展，教师与学生也在发展，因此MPCK中关于学生的知识也在不断变化;又由于MPCK这一内隐的知识要完全显化，不仅需要时间，更需要方法;再加上国际上数学课程改革正如火如荼地进行，且课程改革始终进行着，那么数学主题或问题也会有所变化，教师在某一些主题上的MPCK也会有所变化。因此，MPCK评价工具的完善与发展是一个长期的、艰难的过程。

［1］Shulman L S.Knowledge and Teaching:Foundations of the New Reform［J］.Harvard Educational Review，1987，57(1):1-22.

［2］Hashweh M Z.Teacher Pedagogical Constructions:A Reconfiguration of Pedagogical Kontent Knowledge［J］.Teachers and Teaching:Theory and Practice，2005，11(3):273-292.

［3］Carlson R.Assessing Teachers’Pedagogical Content Knowledge:Item Development Issues［J］.Journal of Personal Evaluation in Education，1990，4(2):157-173.

［4］鲍银霞.TEDS-M对数学教学知识评价工具的研制及启示［J］.课程教学研究，2013(3):28-32.

［5］An Shuhua，Kulm G，Wu Zhonghe.The Pedagogical Content Knowledge of Middle School，Mathematics Teachers in China and the U.S.［J］.Journal of Mathematics Teacher Education，2004，7(2):145-172.

［6］Corleis A，Schwarz B，Kaiser G，et al.Content and Pedagogical Content Knowledge in Argumentation and Proof of Future Teachers:A Comparative Case Study in Germany and Hong Kong［J］.ZDM:The International Journal on Mathematics Education，2008，40(5):813-832.

［7］Manizade A G，Mason M M.Using Delphi Methodology to Design Assessments of Teachers’Pedagogical Content Knowledge［J］.Educational Studies in Mathematics，2011，76(2):183-207.