多拐曲轴疲劳谐振系统的理论与实验分析＊

刘彦臣，庞思勤，王西彬，解丽静

（1.北京理工大学 机械与车辆学院，北京 100081；2.中北大学 机电工程学院，山西 太原 030051）

0 引言

机械产品的安全性和可靠性是技术水平的重要指标，产品设计寿命内的可靠性和失效问题在人类生产生活中产生了重要影响［1-2］.曲轴是内燃机的重要零部件，因其工作中受周期载荷作用，疲劳失效是曲轴的典型损坏形式［3］.目前，曲轴弯曲疲劳实验设备存在两个缺陷：①均为单拐实验机［4-6］，对于多拐曲轴测试只能逐个拐依次实验，且由于装卡问题，相邻的曲拐只能选取一个进行疲劳实验，既浪费了时间，又使曲轴整体寿命计算结果失真；②设备的机械部件调节适应能力差，针对部分谐振频率接近的曲轴组件无法实验.本文的目的在于研究多曲拐谐振实验以及可调谐振频率的曲轴弯曲疲劳实验方法.

1 多拐曲轴疲劳谐振实验系统的结构设计及理论分析

1.1 谐振实验系统的结构原理

多拐曲轴疲劳谐振实验的工作原理如图1 所示，以四拐曲轴为测试工件，摆臂通过与曲轴臂外形匹配的型腔固定在曲轴上，摆臂和被测曲轴组成一个多自由度的谐振系统；激振器在控制柜给定的信号下，通过推杆对摆臂曲轴系统进行激励；摆臂曲轴系统在特定的激励频率下产生共振，实现对被测曲轴的整体弯曲疲劳谐振实验；当被测曲轴产生裂纹，刚度下降时，谐振频率也随之下降，当谐振频率下降1 Hz时终止实验［7-8］，此时的弯曲循环周数即为曲轴的弯曲疲劳寿命.

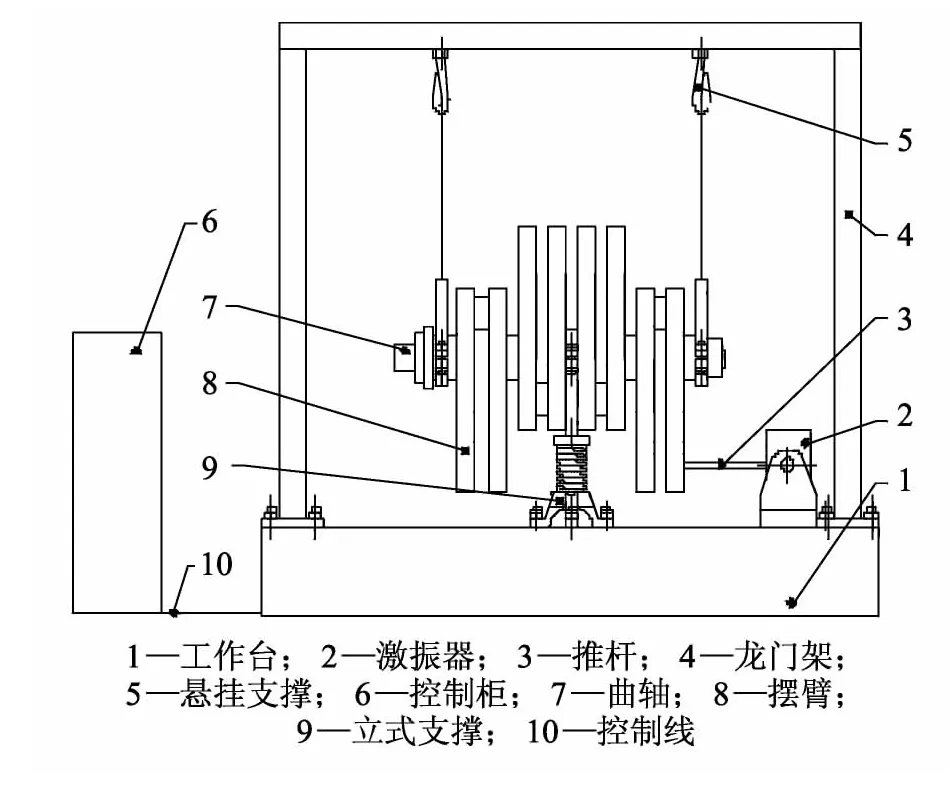
图1 疲劳试验机结构原理Fig.1 Structure principle of fatigue test machine

摆臂的结构如图2 所示，摆臂主体芯部具有与曲轴臂外形吻合的型腔，通过内六角螺钉连接两个摆臂主体，将曲轴臂镶嵌在摆臂主体内，保证了摆臂体和曲轴的固定连接.配重块通过双头螺栓和圆柱销同摆臂主体连接.配重块的作用在于调节谐振频率，提高工作效率.对部分因振型频率接近而无法进行实验的曲轴，配重块有一定范围的调节能力，使实验能够顺利进行.

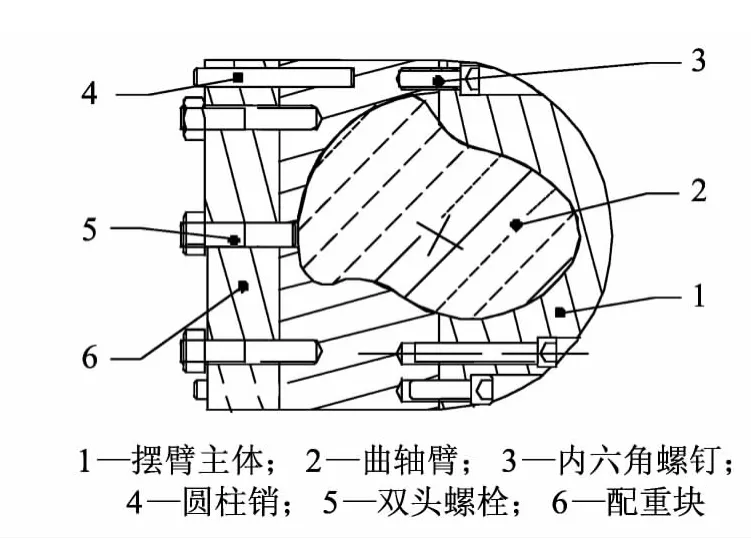
图2 摆臂结构示意图Fig.2 Schematic diagram of swing arm structure

1.2 谐振系统的数学模型

如图3 所示，四拐曲轴的8 个曲轴臂上固定装卡了8 个摆臂，摆臂和曲轴组成一个谐振系统.各摆臂绕各自的振动中心做微小的转动，转角为φ，转动惯量为J.因为摆臂的转动角度微小，所以在理论分析时对图3 所示系统进行了简化.每个摆臂简化为集中质量模块，转角简化为轴向位移.系统的简化模型如图4 所示，f，m，k，c，x分别为各个摆臂的受力、质量、弹性系数、阻尼系数和位移.简化后的系统同图3所示系统具有本质相同的系统特性，即系统的传递函数不变.

图3 谐振系统Fig.3 Resonance system

图4 系统简化模型Fig.4 Simplified model of system

对图4 所示的简化系统进行受力分析，由控制理论知，上述系统为线性定常系统［9-10］.列写系统的微分方程，并写成矩阵形式

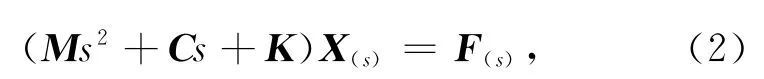
式中：s是拉氏变换因子，为复数.

利用模态分析理论［11］对式（2）解耦.通过系统的无阻尼自由振动方程求取系统的主振型矩阵，由式（2）可得系统的无阻尼自由振动方程

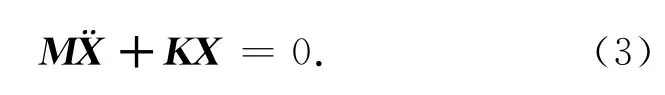
弯曲疲劳系统的激励信号为正弦或余弦函数，由控制理论知，系统的响应是和激励具有一定幅值比和相角差的同频率信号，设xi＝Aisin（wt+φi），i＝1，2，…，8.根据系统的物理特性，研究中图3 所示各摆臂的结构尺寸及材料相同，因此在计算中取图4 所示系统中各质量模块近似相等，m1＝m2＝… ＝m8＝m，弹性系数近似相同，k1＝k2＝… ＝k8＝k，将以上参数代入式（3），解得系统无阻尼固有频率和主振型矩阵

由式（4）可知，谐振系统的固有频率与摆臂质量的平方根成反比，证明通过配重块对摆臂质量的调节，可以实现对谐振系统固有频率的调节.

1.3 谐振系统的频域分析

对系统进行频率响应分析，将s＝jw代入式（2）得

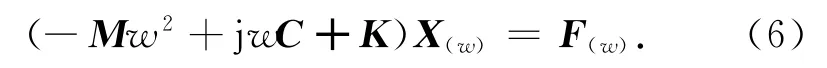
利用主振型矩阵的正交性，对式（6）两边左乘ΦT，令X（w）＝ΦQ（w），Q（w）为模态坐标，Q（w）＝［q1，q2，…，q8］T.可得

对于图1 所示的激励振动系统为单输入的情况，F＝［0，…，0，f8（w）］T，式（7）可以用8 个独立的方程表示

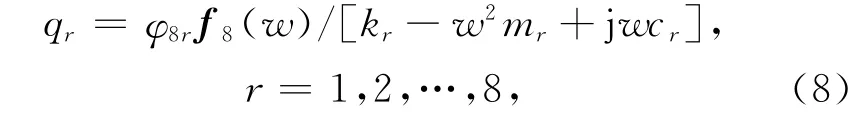
式中：kr，mr，cr分别为模态刚度、模态质量和模态阻尼.由控制理论知，线性定常系统的响应满足叠加原理.对系统中任一摆臂的响应可表示为

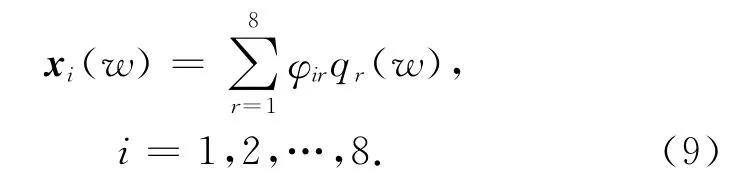
求图1 所示左侧第一摆臂的位移响应，由式（8）和（9）可得

激励点到第一摆臂间的传递函数为

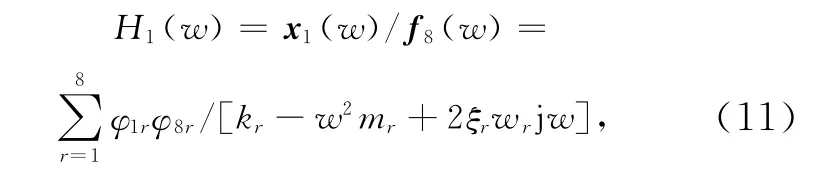
式中：ξr＝cr／2wr为各振型的阻尼系数，可通过模态实验求取，此处根据经验取ξr＝0.05（r＝1，2，…，8），同理可求得其余摆臂至激励点间的传递函数.由此各摆臂的位移输出

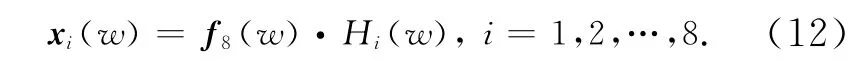
当式（1）中的激励力F＝［0，…，0，时，由式（12）的结果进行反拉氏变换，求得图1 所示系统的稳态强迫振动，见表1.

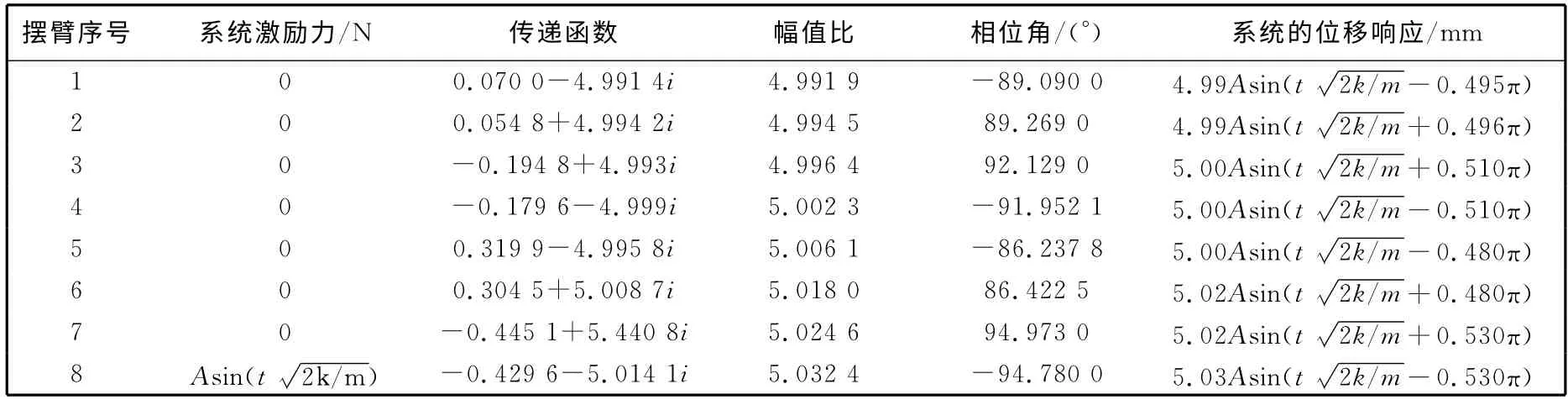
表1 系统的稳态强迫振动Tab.1 Steady forced vbration of system

分析表1 数据得，激励频率是系统的第五阶固有频率，所以系统产生共振，第五阶固有频率主振型占主导地位.由各个摆臂位移响应可以确定谐振振型恰好满足四拐曲轴的弯曲疲劳实验要求，且可以通过配重块调节摆臂的质量m来调节系统的谐振频率.

2 模态测试

针对柴油发动机的四拐曲轴，采用单输入多输出法进行模态测试［11-12］.使用LMS 公司的SC310-VTP型数据采集仪和Impact Testing模块进行数据分析.根据曲轴弯曲疲劳系统的结构特点，在各个摆臂上设置40个敲击点，编号为N1～N40，位置如图5 所示.在各点沿x，y轴方向用力锤敲击，测试时对每个点的采样信号进行10次平均.使用40个加速度传感器采集振动信号，分别安装在各摆臂表面N1～N40处.采样频率选1 280Hz，谱线数为4 096，分辨率为0.312 5Hz.

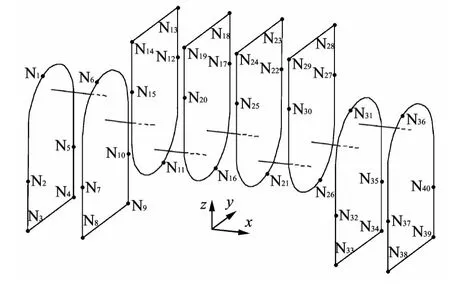
图5 模态测试敲击点示意图Fig.5 Schematic diagram of tapping points of modal test

采用Polymax法［13-15］对测得的各传递函数进行模态参数识别.如图6 所示，测得该四拐曲轴弯曲疲劳谐振系统的非刚体1～6阶模态振型，分别为一阶弯曲、一阶扭转、二阶弯曲、三阶弯曲、四阶弯曲和二阶扭转.因为一阶扭转和二阶扭转在x轴方向的位移为零，所以扭转振型未在图6中列出.由图6可知，相应的振型互相吻合，四阶弯曲振型是谐振系统最理想的振型，可实现4 个曲拐的弯曲疲劳谐振实验.谐振系统的1～6 阶固有频率和阻尼比见表2.

将模态测试结果与频域分析结果进行对比，可知通过激振器对曲轴谐振系统施加369 Hz 的激励力时，四拐曲轴系统摆臂做反向四阶弯曲振动.该谐振频率与相邻的谐振频率差较大，不会引起其他振型的谐振，多拐弯曲疲劳谐振实验可以顺利进行.

表2 曲轴系统的模态参数Tab.2 Modal parameters of crankshaft system

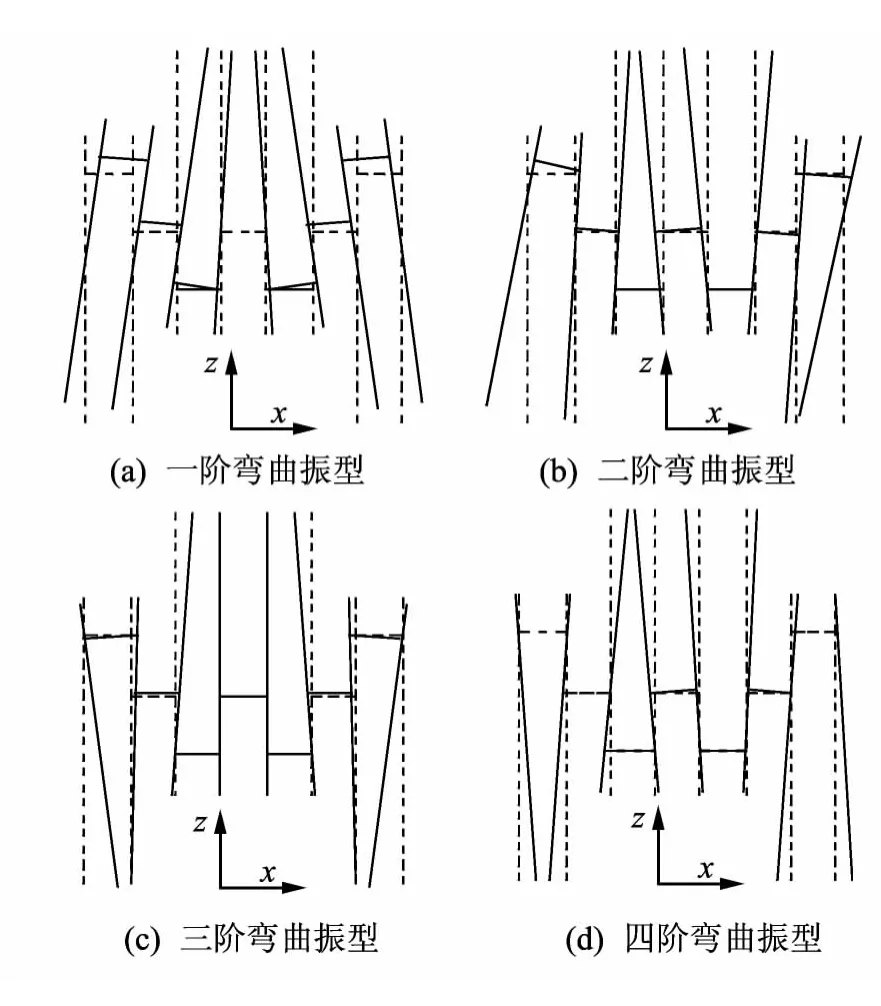
图6 谐振系统模态测试弯曲振型结果Fig.6 Bending mode result of modal test in resonance system

3 结论

1）针对现有曲轴疲劳实验机存在的问题，提出了多曲拐弯曲疲劳的谐振实验方法.通过对系统数学模型的理论分析，证明了系统的固有频率可以由配重块的质量来调节，使谐振系统可以在一定范围内选择较理想的工作频率.

2）对四拐曲轴弯曲疲劳谐振系统进行了频率响应分析，结果表明在第五阶固有频率激励时，系统产生共振，四阶反向弯曲振型居主导地位，满足多曲拐疲劳实验要求.

3）采用模态测试方法获得了同理论分析相同的结果，四阶反向弯曲振型满足多拐曲轴弯曲疲劳的谐振实验要求，表明上述多拐疲劳谐振实验方法切实可行.

［1］姚卫星.结构疲劳寿命分析［M］.北京：国防工业出版社，2003.

［2］李守新，翁宇庆，惠卫军，等.高强度钢超高周疲劳性能［M］.北京：冶金工业出版社，2010.

［3］俞小莉，周迅.智能型曲轴弯曲疲劳试验系统［J］.兵工学报，2004，25（3）：368-371.Yu Xiaoli，Zhou Xun.An intelligent fatigue test system for crankshaft［J］.Acta Armamentarii，2004，25（3）：368-371.（in Chinese）

［4］Vogwell J.Analysis of a vehicle wheel shaft failure［J］.Engineering Failure Analysis，1998，5：271.

［5］Silva F S.Analysis of a vehicle crankshaft failure［J］.Engineering Analysis，2003，10：605-616.

［6］Asi O.Failure analysis of a crankshaft made from ductile cast iron［J］.Engineering Failure Analysis，2006，13：1260-1267.

［7］Aramcharoen A，Mativenga P T.White layer formation and hardening effects in hard turning of H13tool steel with crtialn and crtialn most-coated carbide tools［J］.International Journal of Sustainable Manufacturing，2008，36：650-657.

［8］Watmough T，Malatesta M J.Strengthening of ductile iron for crankshaft applications［C］.Proceedings of Expendable Pattern Casting：Managing the Technology，AFS，1993.

［9］陈小异，孔晓红.机械工程控制基础［M］.北京：高等教育出版社，2010.

［10］杨叔子.机械工程控制基础［M］.武汉：华中科技大学出版社，2011.

［11］傅志方，华宏星.模态分析理论与应用［M］.上海：上海交通大学出版社，2000.

［12］Spiteri P.，Ho S.，Lee Y L.Assessment of bending fatigue limit for crankshaft sections with inclusion of residual stress［J］.International Journal of Fatigue，2007，29（2）：318-329.

［13］鲍珂.曲轴弯曲疲劳模拟试验与数值计算研究［D］.北京：北京理工大学，2011.

［14］王佳.基于PolyMAX 法的齿轮箱试验模态分析［J］.机械传动，2013，37（2）：66-75.Wang Jia.Modal analysis of gearbox based on the method of PolyMAX［J］.Journal of Mechanical Transmission，2013，37（2）：66-75.（in Chinese）

［15］高云凯.基于PolyMAX 的声固耦合模态试验研究［J］.振动与冲击，2013，32（2）：158-163.Gao Yunkai.Acoustic-structure coupled modal test based on PolyMAX［J］.Journal of Vibration and Shock，2013，32（2）：158-163.（in Chinese）