强预不变凸函数

王海英，符祖峰，杨筱珊

(安顺学院数理学院，安顺 贵州561000)

0 引言

在最优化理论、管理科学、对策论及工程中，凸集及凸函数都起着相当重要的作用.近年来，关于凸性及其各种形式的推广的研究成果越来越多(见［1-9］及其中的参考文献).1988年，Weir和Mond在文献［4］中引入了不变凸集，随后Weir和Jeyakwmar在文献［5］中提出了预不变凸函数的概念，并且研究了它们的若干性质及应用.2001年，Yang和Li在文献［6］中又给出了预不变凸函数的其它一些性质.颜丽佳和刘芙萍在文献［7］中讨论了半连续函数与强预不变凸函数的关系，秦春蓉在文献［8］中通过对文献［7］中定理条件的削弱得到了同样的结论.

受以上研究成果的启发，本文对强预不变凸函数作了进一步研究，在更弱的条件下讨论半连续函数与强预不变凸函数之间的关系，简化了强预不变凸函数一些性质定理的证明.并进一步给出强预不变凸函数在数学规划问题中的两个应用，从而完善了对此类广义凸函数的研究，这些结果也丰富了广义凸性理论.

1 预备知识

在本文我们约定X⊆Rn，f:X→R和η:Rn×Rn→Rn是两个函数.

定义 1.1［7］如果∀x，y∈X，∀λ∈［0，1］有

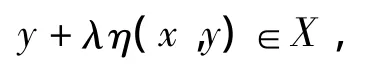
则称X是不变凸集.

定义 1.2［7］设 X 是不变凸集，如果∀x，y∈X，∀λ∈［0，1］有

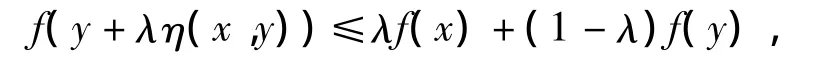
则称f是预不变凸函数.

定义 1.3［7］设 X 是不变凸集，如果∀x，y∈X，∀λ∈［0，1］，存在 β ＞0，使得

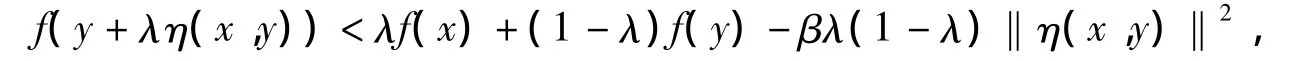
则称f是强预不变凸函数.

条件 C［7］若∀x，y∈X，∀λ∈［0，1］有，

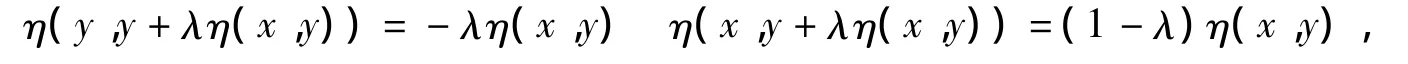
则称η满足条件C.

条件D［7］设X是不变凸集，若∀x，y∈X有则f称满足条件D.

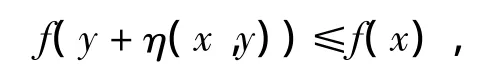
条件 H［7］设 X 是不变凸集，如果 λn∈［0，1］且 λn→λ，则∀ε ＞0，∃正整数 N，当 n ＞N 时，对∀x，y∈x都有

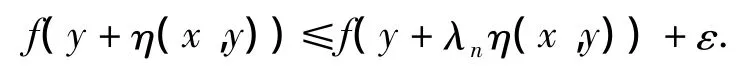
则f称满足条件H.

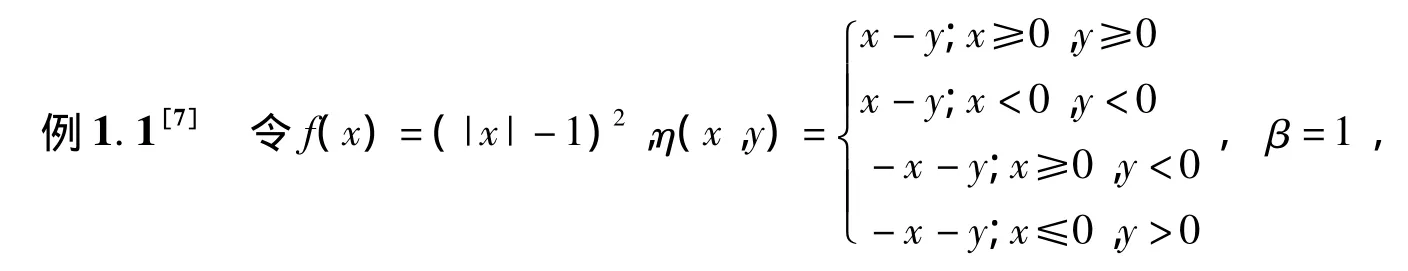
则f是强预不变凸函数.

2 主要结果

本节我们将在适当的条件下，分别建立强预不变凸函数与上半连续函数和下半连续函数之间的关系，简化强预不变凸函数一些性质定理的证明.同时给出强预不变凸函数在数学规划中的两个重要应用.

定理2.1 设X是不变凸集，f上半连续且满足条件D，η满足条件C，则f是强预不变凸函数，当且仅当，∃α∈(0，1)，使得对任意∀x，y∈X，存在 β ＞0 有

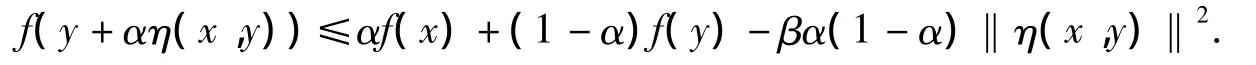
证明 事实上，我们只需证明充分性.假设f不是强预不变凸函数，则∈(0，1)和β ＞0，对∀x，y∈X有

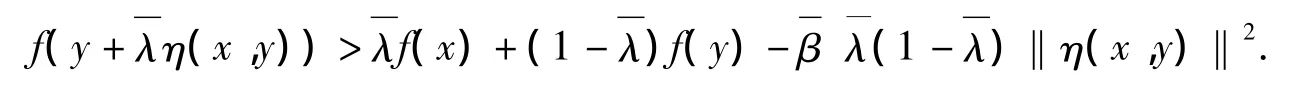
令

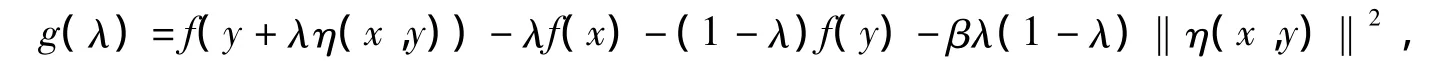
因f上半连续，则g(λ)在［0，1］上也上半连续，从而由上半连续函数在紧集上可取得最大值的结果知，g(λ)在［0，1］上存在最大值 M0.令

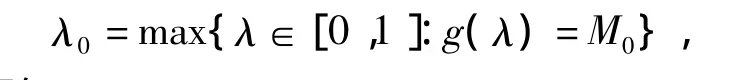
易知g(0)=0，由f满足条件D可知

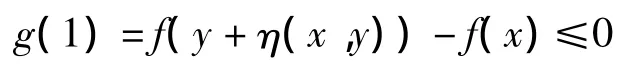
因而 λ0∈(0，1).

选取 δ，使得

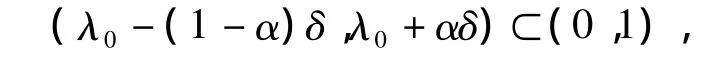
令

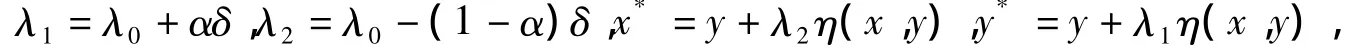
由η满足条件C有

从而

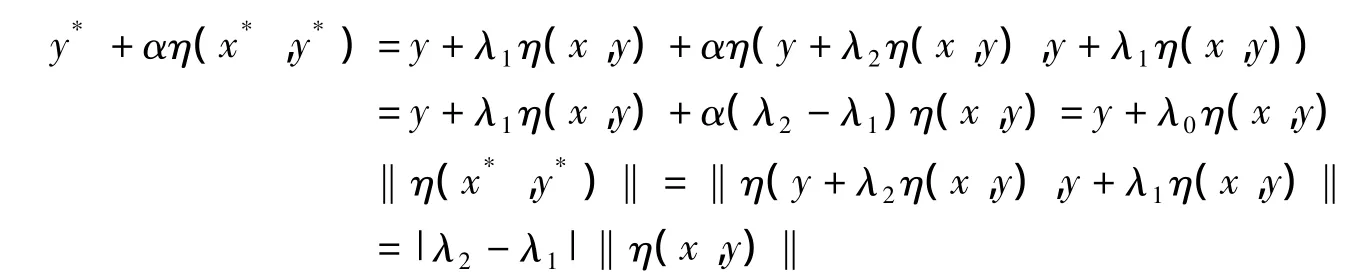
我们有

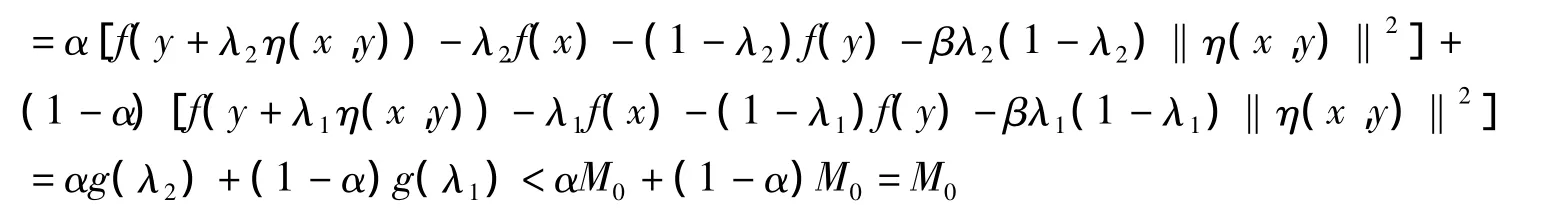
矛盾，故f是强预不变凸函数.

定理2.2 设X是不变凸集，f下半连续则f是强预不变凸函数，当且仅当，∃α∈(0，1)，使得对任意∀x，y∈X，存在 β ＞0 有

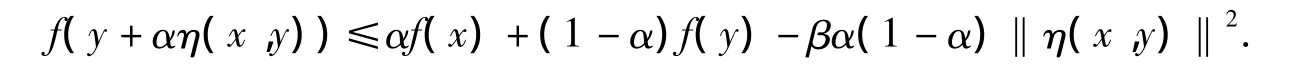
证明 事实上，我们只需证明充分性.

令

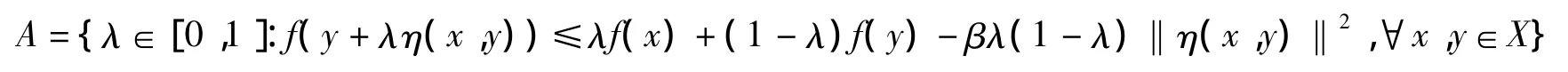
如果 λn∈A 且 λn→λ，则由 A 的定义，对∀x，y∈X，有

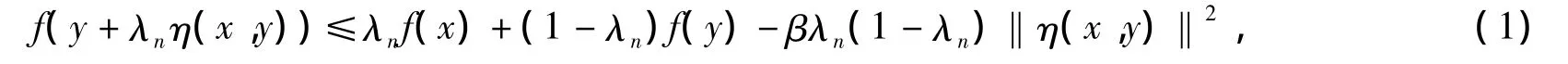
又f下半连续，则f满足条件H，即对∀ε＞0，∃正整数N，当n＞N时，对∀x，y∈X都有

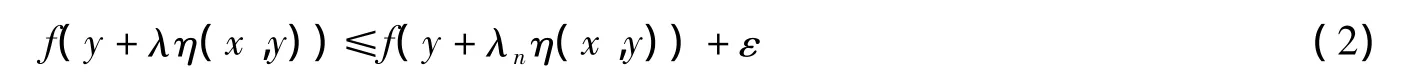
由(1)、(2)可得

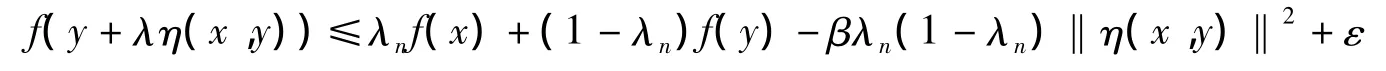
再由λn→λ和ε的任意性，有

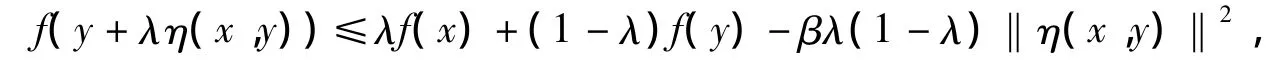
即f是强预不变凸函数.

注2.1 定理2.1、定理2.2没用到文献［7］中X是开集这一条件.

注2.2 定理2.2排除了文献［7］中集合A在［0，1］上的稠密性.

考虑下面的数学规划问题:

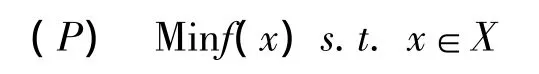
因f是强预不变凸函数，从而对于∀λ∈［0，1］有，

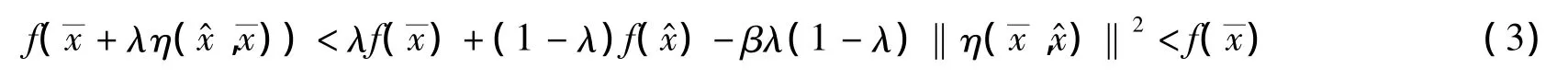
当λ充分小时，我们有

(2)唯一性证明.假设x0，x1∈K为规划问题(P)的两相异全局最优点，则x0≠x1且f(x0)=f(x1).由于 X 是不变凸集，则对于∀λ∈［0，1］，x0+λη(x1，x0)∈X.因 f是强预不变凸函数，从而有

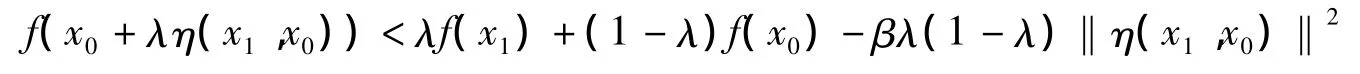
当 x0≠x1，由条件 C 有 η(x0，x1)≠0，从而

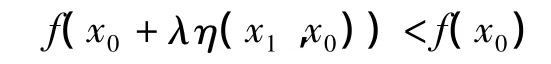
这与x0是规划问题(P)的全局最优解矛盾，因此规划问题(P)的全局最优解唯一.

定理2.4 设X是不变凸集，f是强预不变凸函数，则规划问题(P)的最优解集是不变凸集.

证明 设x，y是规划问题(P)的两相异解，由于X是不变凸集，即对于∀λ∈［0，1］，有z=y+λη(x，y)∈X.因f是强预不变凸函数，从而有

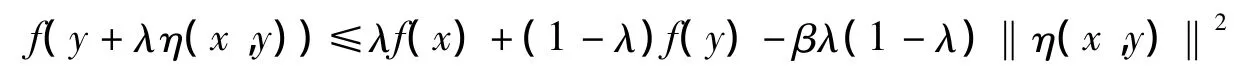
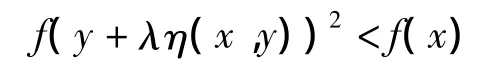
当 x≠y，由条件 C 有 η(x，y)≠0，从而于是z=y+λη(x，y)也是规划问题(P)的最优解，所以规划问题(P)的最优解集是不变凸集.

注2.3 定理2.3和定理2.4不但可以看作是强预不变凸函数的两个很好的性质，而且给出了强预不变凸函数在极小化问题中的应用，从而说明了强预不变凸函数在数学规划中也有着非常重要的意义和地位.

［1］A.Cambini，E.Castagnoli，L.Martein，et al.Generalized Convexity and Fractional Programming with Economic Application［M］.Springer-Verlag，Berlin.1990.

［2］J.P.Crouzeix，J.E.Martinez-Legaz，M.Volle.Generalized Convexity，Generalized Monotonicity(proceedings of the Vth international workshop on generalized convexity，Marseille.French，July 17-21，1996)［M］.Springer-Verlag，Berlin.1994.

［3］S.Schaible，W.T.Ziemba.Generalized Concavityin optimization and Economics［M］.Academic Press，New York，1981.

［4］T.Weir，B.Mond.Prieinvex functions in multiple objective optimization［J］.Journal of Math Anal and Appl.1988，136:29 ～38.

［5］T.Weir，V.Jeyakwmar.A class of nonconvex functions and mathematical programming［J］.Bulletin of Australian Mathematical Society，1988，38:177～189.

［6］X.M.Yang，X.Q.Yang，K.L.Teo.Characterizations and applications of prequasiinvex functions［J］.Journal of Optimization Theory Applications.2001，110(3):645 ～668.

［7］颜丽佳，刘芙萍.强预不变凸函数［J］.重庆师范大学学报(自然科学版).2005，22(1):11～15.

［8］秦春蓉.强预不变凸函数的性质［J］.重庆师范大学学报(自然科学版).2006，23(3):1～4.

［9］双立青.多目标规划在广义凸性下的最优化条件的研究［D］.武汉科技大学，2007.