非线性方程数值解法的研究

谭振江，肖春英

(吉林师范大学计算机学院，吉林四平136000)

0 引言

随着现代计算机科学技术的迅猛发展，一些非线性方程模型在实际问题中频频出现.经常要求非线性方程f(x)=0的根，方程f(x)=0的根叫做函数f(x)的零点.很多我们非常熟悉的线性模型都是一定条件下的非线性问题简化得到的.由于非线性方程在各个科学领域与工程计算等领域中地位越来越重要，因此我们有必要就有关非线性方程的解法做一些探讨和研究.

由于非线性方程有其自身的复杂性，在除了少数特殊的非线性方程外，直接法求得结果的情况是不可能的，这时我们需要借助于牛顿迭代法、二分法和弦截法进行近似求解.本文简要的分析了这些数值算法的计算效果，适用范围以及优劣性等特点，运用实例化进行系统分析［1-3］.

(1)引入一个非线性方程的例子，运用三种思想分别进行分析，得到三种解法的根本思想;

(2)把数学方法与数学思想提取出来，同时对该数学方法进行一定程度上的理解;

(3)给出各种算法的循环思想以及相应的程序实现流程图，展现出一个清晰明了的框架;

(4)基于c语言的基础上，写出可执行的程序.

1 三种解法的简单概述

牛顿迭代法(Newton’s method)(又称为牛顿—拉夫逊方法(Newton-Raphson method))，它是牛顿提出的关于实数域和复数域上近似求解方程的一种方法.多数方程不存在直接的求根公式，想要求出其精确根非常困难，甚至不可能，从而寻找方程的近似根就显得格外重要.牛顿迭代法是一种重要和常用的迭代法，使用函数f(x)的泰勒级数的前面几项来寻找f(x)=0方程的根.其基本思想为将非线性函数f(x)逐步线性化，继而将非线性方程f(x)=0的求解近似地转化为线性方程求解.此方法广泛用于计算机编程中.

二分法(或称对分法、二分区间法)，是求方程f(x)=0近似解的一种常用的简单直观的方法.设函数 f(x)在闭区间［a，b］上连续，且 f(a)f(b)＜0，则根据连续函数的性质可知，f(x)=0在(a，b)内务必有实根，称区间［a，b］为有根区间，这是高等数学微积分中的介值定理，也是二分法可以使用的前题条件［4-5］.

弦截法也是一种求方程根的基本方法，在计算机编程中有广泛应用.它的基本思想是:任取两个数x1、x2，求得其所对应的函数值 f(x1)、f(x2).如果两函数值同号，则重新取数，直到这两个函数值异号为止.连接(x1，f(x1))与(x2，f(x2))这两点形成的直线与x轴相交于一点x，求得对应的f(x)，判断其与f(x1)、f(x2)中的哪个值同号.如f(x)与f(x1)同号，则f(x)为新的f(x1).将新的f(x1)与f(x2)连接，如此进行循环.这里体现的是极限的思想［6］.

2 三种解法的实例化分析过程

2.1 牛顿迭代法

实现牛顿迭代法的数学思想的基本步骤如下:

(1)给出初始近似根x0及其精度e;

牛顿迭代法对于初值的选取尤其重要，初值要求必须足够接近精确值才能保证局部收敛.

(2)计算x1=x0-f(x0)/f'(x0);

(3)若|x1-x0|＜0，转向(4);否则 x0=x1，转向(2);

(4)输出满足精度的根x1，结束.

算法流程图如图1所示.

实例:用牛顿迭代法求方程在1.5附近的根:

程序输出结果，如图2所示.

图2 牛顿迭代法的程序输出结果

2.2 二分法

二分法是求方程近似根的方法中行之有效的最简单的方法，它的递推过程简单易行，便于计算机上实现.

实现二分法的数学思想的基本步骤如下:

(1)输入有根区间的端点a，b及预先给定的精度e;

二分法确定有根区间的一般方法:为了确定方程根的初值，必须圈定根所在的范围，即圈定根(或称根的隔离);在此基础上，采用恰当的数值方法确定有一定精度要求的初值;关于代数方程，根的个数(实根或复根)与其次数相同.对于超越方程，其根的个数可能是一个、几个或者无解，没有固定的圈根方法［7-8］.

(2)计算x=(a+b)/2;

(3)若 f(a)f(x)＜0，则b=x;否则a=x;

(4)若 |b-a|＜e，则输出方程满足精度要求的根x，则计算结束;否则转(2).

二分法算法流程图如图3所示.

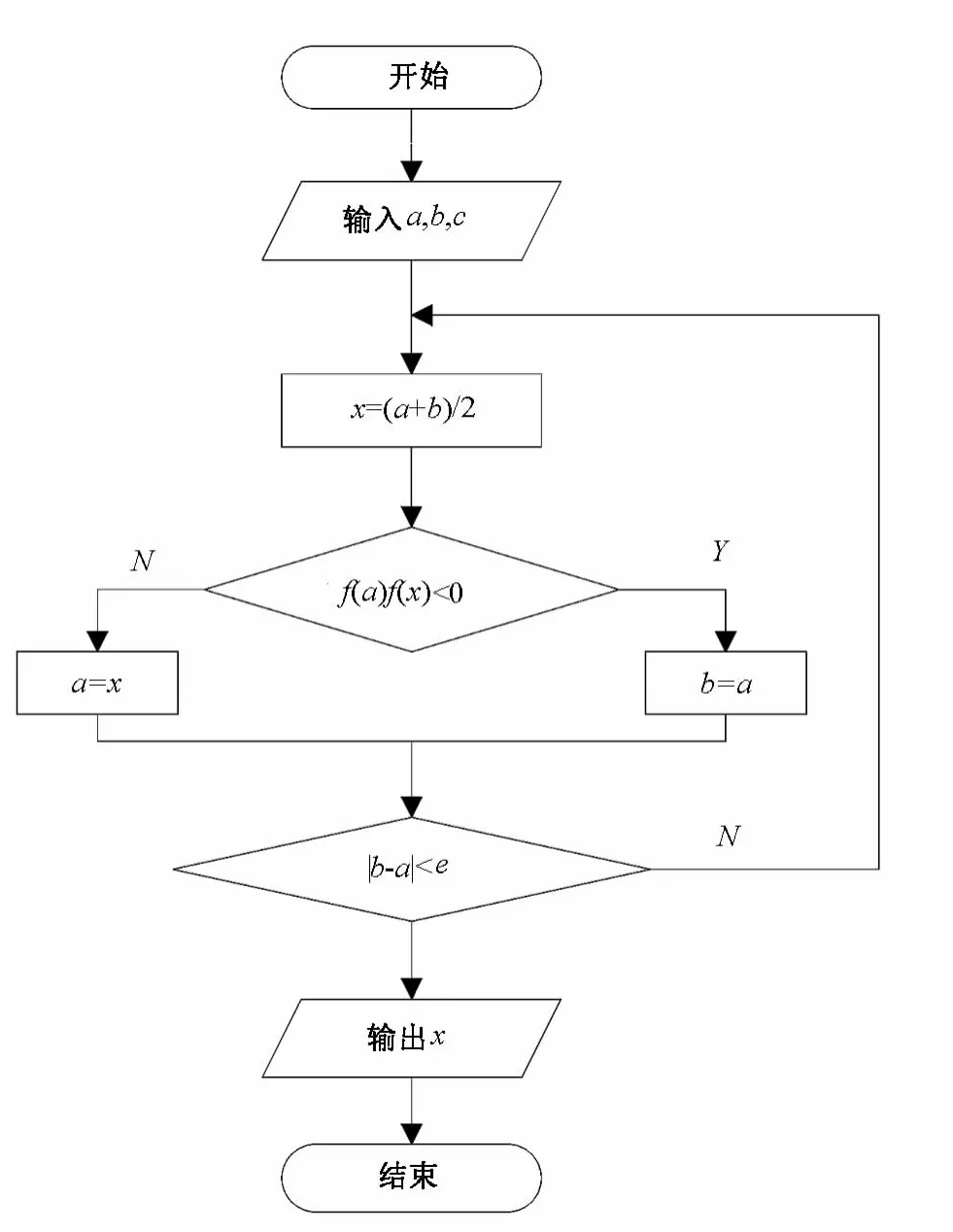
图3 二分法算法实现流程图

实例:用二分法求方程在(-10，10)之间的根:2x3-4x2+3x-6=0.

程序输出结果如图4所示.

图4 二分法程序输出结果

2.3 弦截法

实现弦截法的数学思想的基本步骤如下:

(1)选择迭代的初始值x0，x1及其精度e;

(2)计算x2=x1-(f(x1)(x1-0)/f(x1)-f(x0));

(3)若|x2-x1|＜0，转向(4);否则 x0=x1，x1=x2，转向(2);

(4)输出满足精度的根x2，结束.

弦截法算法流程图如图5所示.

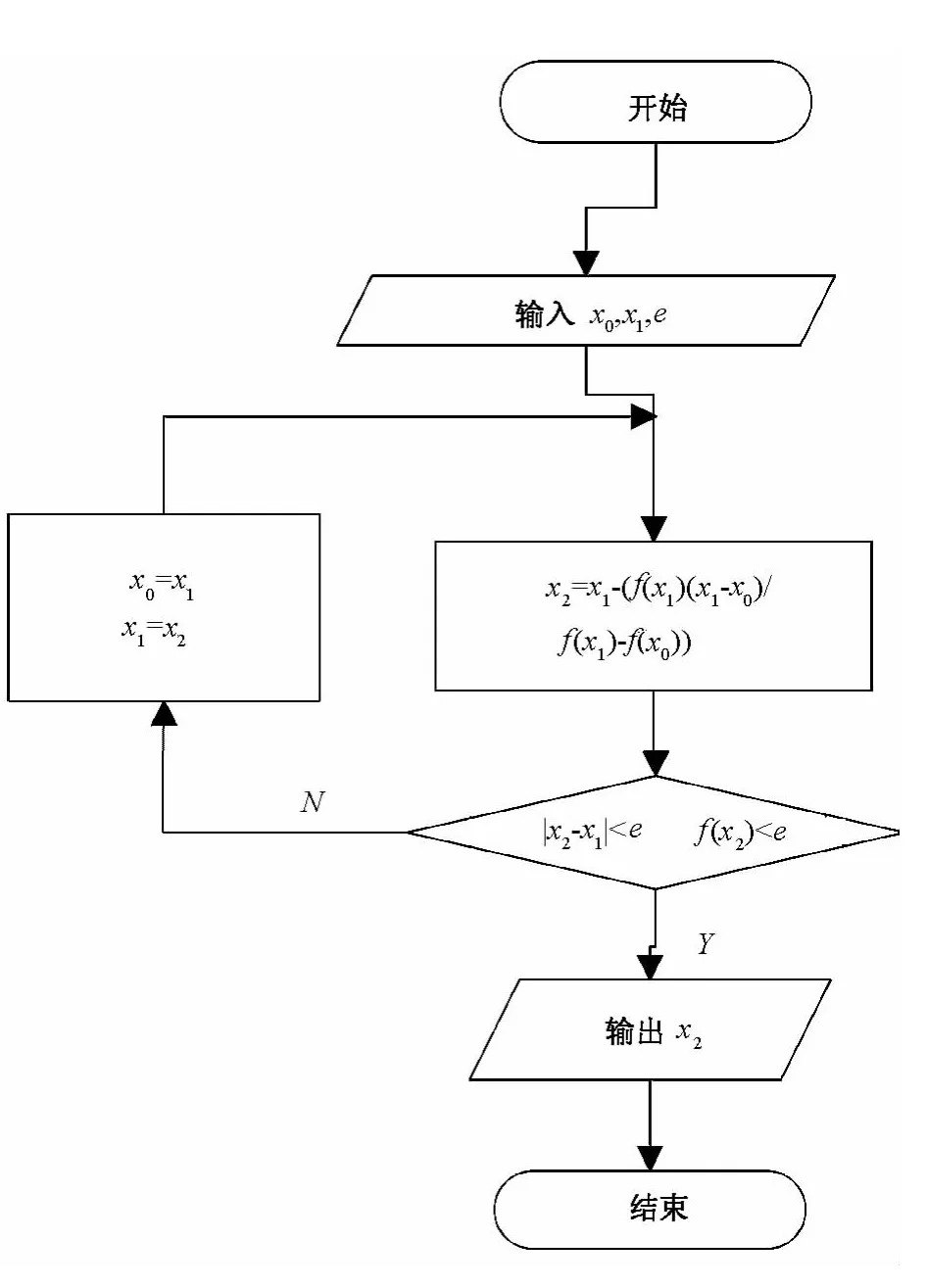
图5 弦截法算法实现流程图

实例:用弦截法求方程2x3-4x2+3x-6=0的根.

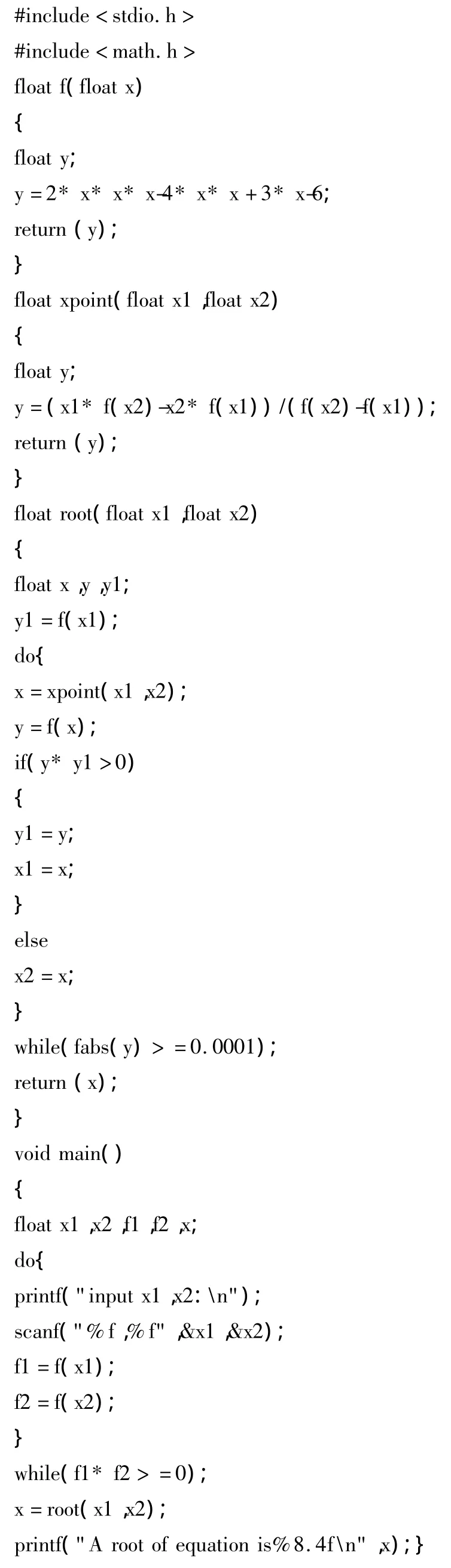
程序输出结果如图6所示.

图6 弦截法程序输出结果

3 结语

通常非线性方程根的数值解法大致分为3个步骤进行:首先判定根的存在性.即方程有没有根存在，如果有根，有几个根;其次确定根的分布范围.即将每一个根用区间隔离开来;获得方程各根的初始近似值;最后进行根的精确化，根的初始近似值按某种方法逐步精确化，直到满足预先要求的精度为止.迭代法具有计算精度高收敛速度快的优点，但是需要计算导数或者矩阵逆的情况，具有一定程度的局限性.针对不同特点的非线性方程选择不同的解法或者不同解法的综合使用，探讨出一种高效率解法，以便使方程达到快速准确求解［9-12］.

［1］高虹霓，曹泽阳.一种新的非线性方程求根迭代法［J］.空军工程大学学报，2002，3(2):84～86.

［2］郭春石，段学新.生化系统的极限环的数值计算研究方法［J］.吉林师范大学学报(自然科学版)，2004，25(3):36～37.

［3］文 武.一阶非线性微分方程解法的探讨［J］.达县师范高等专科学校学报(自然科学版)，2005，15(5):10～11.

［4］周德亮，陈 跃.MATLAB使用中的几个问题的解决方法［J］.吉林师范大学学报(自然科学版)，2007，28(1):19～20.

［5］黄宽娜，刘 徽，李木华.基于信息技术的高等数学实验教学模式研究［J］.西南师范大学学报，2011，36(2):210～215.

［6］刘 滔.牛顿法在架空导线应力计算中的应用［J］.科技风，2010，23:212，220.

［7］郭曦娟.Jacobi和Gauss-Seidel迭代法收敛性的判定［J］.东北重型机械学院学报，1995，19(1):78～82.

［8］程小力.牛顿法的收敛性［J］.浙江工业大学学报，1997，25(3):230～235.

［9］仝秋娟.几种特殊线性方程组的解法研究［D］.西安:西安电子科技大学，2012.

［10］陶 会，曾德强，覃燕梅.求解非线性方程组的一种新的数值解法［J］.内江师范学院学报，2012，27(10):11～13.

［11］朱 宏，付 军.一类Lienard方程周期解的稳定性［J］.吉林师范大学学报(自然科学版)，2006，27(1):70～71.

［12］夏林林，户晗蕾，吴开腾.非线性方程组数值方法的研究进展［J］.内江师范学院学报，2013，28(10):12～17.