数据挖掘在事业单位绩效工资管理中的应用

李广霞， 崔 哲

（1.石家庄经济学院 信息工程学院，河北 石家庄 050031；2.河北师范大学附属中学 信息处，河北 石家庄 050016）

在事业单位（如高校）的绩效工资管理中，不同层次的职工标准不同，只有满足各种条件，职工才能享受相对应的绩效工资.在绩效工资的计算过程中，引入数据挖掘技术可以提高计算效率.根据对职称层级和每个层级对应等级的划分，可以确定职称的分级个数，也就是聚类个数.在传统的k－means算法中，聚类的初始中心点是人为指定的，这容易使聚类的结果趋向局部最优，且往往不准确.本文以高校的绩效工资管理为例，针对k－means算法存在的问题［1］，通过聚类算法中改进的k－means算法［2－4］，采用基于距离和密度的方式确定初始聚类中心［5］，将同一等级职工聚集到同一类中，减少重复计算，给出满足各类的分界点数据，提高聚类的准确率.

1 改进的k－means算法

改进后的算法简称为DSk－means（Distance and Density based k－means）算法.过程如下：

输入，聚类数目k，对象属性个数attr，领域半径δ，领域包含的最少对象数MinPts；

输出，满足条件的k个聚类；

步骤1，计算对象i和j之间的距离d［i，j］；

步骤2，计算每个对象的δ邻域内的对象数x，若x≥MinPts，则将该对象加入高密度区域；

步骤3，从高密度数据集中找出δ邻域内对象个数最多的对象c1，即最高密度的对象，并将其加入初始聚类中心集合Cluster；

步骤4，查询数据集中所有对象到c1的距离，将离c1最远的对象c2放入初始聚类中心集合Cluster，并将其从数据集中删除；

步骤5，从数据集中找出与c1，c2的距离之和最大的对象c3，放入初始聚类中心集合Cluster，并将其从数据集中删除；

步骤6，重复步骤5的操作，直到找到第k个初始聚类中心；

步骤7，以得到的k个聚类中心为出发点，使用k均值算法，以聚类中心不变为结束条件，得到聚类结果.

2 数据预处理

聚类中所用到的数据集包括表1－表4的相关内容.

表1 人员信息表

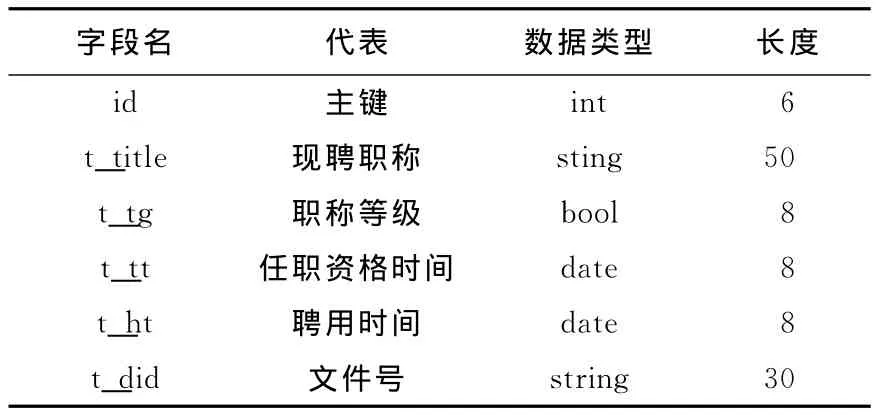
表2 职称信息表

表3 教学、科研工作量

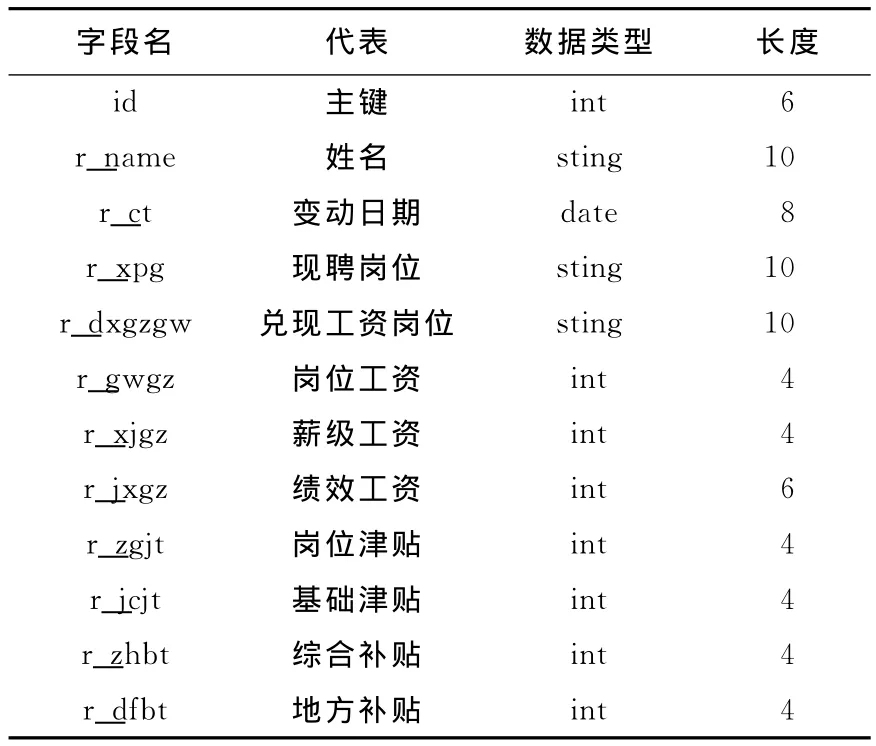
表4 在编人员工资表

2.1 数据选择

在数据挖掘中，首先要进行数据选择.本文的研究对象主要是高校在编的专业技术人员，因此，要选取该类人员教学和科研方面的内容，并设置相应的权重，将教学与科研有机结合，得出该类人员的业绩数据集，如表5所示.

表5 业绩数据表

2.2 数据清理和格式化

对于新进人员和即将退休人员，其在当年的教学工作量和科研工作量均不饱满，在数据挖掘中这些数据属于干扰项，因此要先对数据集中的噪声数据和缺失值进行清理，再去除无关属性，如姓名、职称等，最终得到的数据表如表6所示.

表6 合成后数据集属性

数据集中的出生日期和工作时间两个属性需要进行格式化，分别转换为年龄和工龄.格式化后的数据如表7所示.

表7 格式化后的数据表

由于数据集中的属性变量均为连续型数据，两个数据点之间的距离采用欧几里德距离公式，例如，182098和195209之间的距离为：

3 聚类的实施

本文以正高级职称的聚类过程为例，说明聚类实施的过程.首先，根据文中第2部分所提供的数据集，获取正高级职称人员的相关信息，包括基本信息、职称信息、教学和科研信息以及工资信息，生成正高级人员信息表；其次，去除表中的噪声数据和不完整数据，格式化表中的出生日期和工作日期，并将其分别转换为年龄和工龄；再次，运用本文的算法进行聚类，在聚类的过程中，参数δ和MinPts根据经验设置为30和10，对应的正高级岗位为4级，因此绩效也分为4级，参数k为4.

4 结果与分析

正高职称数据集的聚类结果（迭代6次，耗时120ms）如表8所示.该类人员各个属性的取值范围见表9.

表8 正高聚类结果

表9 正高属性取值范围

由表8、表9可以看出，绩效不仅考虑教师的教学和科研情况，还要考虑其他多方面的因素，比如教师的年龄.从表9可以看出，正高级职称绩效分级有如下标准：教学工作量高于601.81并且科研工作量高于348.35，可享受一级绩效工资；教学工作量高于517.94并且科研工作量高于356.44，可享受二级绩效工资；教学工作量高于513.95并且科研工作量高于215.92，可享受三级绩效工资.对于年龄大的教师，其教学工作量和科研工作量可根据绝对工作量和年龄的具体情况适当调整.

5 结论

本文将改进后的k－means算法引入绩效工资管理中，利用数据挖掘的特点从大量数据中寻找规律，为绩效工资的计算提供了更加完善的方法，但改进后的算法在参数δ和MinPts的选择上仍需提高.

［1］符保龙.基于混合遗传克隆算法的关联规则挖掘 ［J］.计算机工程，2009，35（22）：216－217.

［2］刘华婷，郭仁祥，姜浩.关联规则挖掘Apriori算法的研究与改进 ［J］.计算机应用与软件，2009，26（1）：146－149.

［3］张净，孙志挥，宋余庆，等.基于信息论的高维海量数据离群点挖掘 ［J］.计算机科学，2011，38（7）：148－151.

［4］钱雪忠，孔芳.关联规则挖掘中对Apriori算法的研究 ［J］.计算机工程与应用，2008，44（17）：138－140.

［5］贺志，黄厚宽.一种优化相关规则的发现 ［J］.计算机学报，2006，29（6），906－913.