小波分析在天然地震初震及震相识别中的应用

李红星， 赵烽帆， 郑敏娜

(1. 东华理工大学核工程与地球物理学院，江西 抚州 344000;2. 中国地震台网中心，北京 100045;3.东华理工大学外国语学院，江西 抚州 344000)

我国是个多地震发生国家，由地震造成的人员伤亡与经济损失十分巨大，为了充分发挥观测台站在防震减灾中的直接作用和提升我国现有震害预测系统的层次，也迫切要求开展与此相关的科学技术问题的研究。其中地震波的震相识别是研究的基础。在该方向上的研究具有非常重要的意义。地震波震相识别是现代地震学研究中的重要课题，它是地球内部构造、地震定位、震源机制等一系列研究的基础。震相是地震波特性加上地震仪频率特性双重制约之下出现在地震记录图上的有意义的点位和特定时域的线段。震相识别传统的人工识别方法主要有:直观检验法、达曲线检验法、走时表检验法、综合检验法、合成地震图检验法等。这些方法都是靠识别者的经验来判断、识别，不仅费时，而且会有人为的误差、读数错误等等都会影响识别的精度，地震预警与基于震害快速评估的震后应急反应系统的出现，只靠人工识别是非常低效和不切合实际的，因此必须研究和发展稳定、实用和高效的自动识别方法和系统。

分析平稳信号的理想工具是傅里叶变换。对于非平稳信号，傅里叶变换不再是有效地工具，因为其无法描述信号的局部频率特性。而小波变换正是分析非平稳信号的有力工具之一(秦渝清等，1995;刘希强等，1998;周彦斌，2007)。小波变换是傅里叶变换的新发展，它既保留了傅里叶变换的优点，又弥补了傅里叶变换在信号分析上的一些不足(郑沿真等，2001;冉启文，2001;刘希强等，2002)。小波变换的概念是由法国从事石油信号处理的工程师J.Morlet 在1974年首先提出的。早在七十年代，A.Calderon 表示定理的发现、Hardy 空间的原子分解和无条件基的深入研究为小波变换的诞生做了理论上的准备。1986年数学家Y. Meyer 偶然构造出一个真正的小波基。小波变换是一个时间和频率的局网域变换，因而能有效的从信号中提取资讯，通过伸缩和平移等运算功能对函数或信号进行多尺度细化分析，解决了Fourier 变换不能解决的许多困难问题，从而小波变化被誉为“数学显微镜”。针对地震波记录是非稳态信号的特点，1982年勘探地球物理学家Morlet 等首次将小波变换引进地球物理研究领域(王大凯等，2006;Kanwaldip et al.，1997)。1992年，Mallat 给出了一种利用小波变换模极大值识别奇异点的方法，它是通过搜索小波变换的模极大值点来寻找其突变点，这种方法已经被广泛地运用在诸如故障检验，图像识别等许多领域，取得了较好的效果(强琳等，1997;Hou et al.，2006;杨凯新等，2004)。我国刘希强等将小波变换方法应用在震相识别方面，这些方法只是对地震波数据用小波变换进行预处理，加大信号信噪比，对于信噪比较大的小波变换系数再进行突变点的识别。

本文应用小波包和小波变换对地震信号震相与初至进行综合分析，首先对信号进行小波包变换，识别信号的初至时间，然后用小波变换对信号进行小波分解，得到小波分解细节信号，得出信号频率的分部情况，进而识别出初至位置的震相。先用该方法对模拟信号进行识别，验证它的有效性和准确性，最后通过汶川大地震余震地震信号的处理，有效的识别了天然地震震相及其初至时间。

1 信号震相及初至识别原理

1.1 基于小波包变换初至识别原理

1.2 基于小波变换信号震相识别原理

信号f(t)的小波变换:

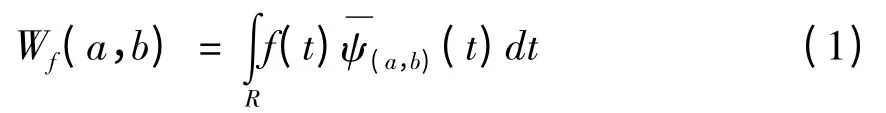
小波变换提取的是f(t)在时间点t = b 附近和频率点附近时频窗:［b -| a | Δ(ψ)，b中的那部分时频信息。具体地说，信号f(t)的小波变换Wf(a，b)自适应地提取原信号在“时间段”［b -|a| Δ(ψ)，b +| a | Δ(ψ)］内和“频带”的时频信息。所以，从信号f(t)到小波变换Wf(a，b)实际上是把信号在时间域局部化到范围［b -| a| Δ(ψ)，b +| a| Δ(ψ)内，且在频率域局部化到范围内。这体现的正是小波变换特有的能够实现时间局部化同时频率局部化的时频局部化能力。小波分析把信号分解为两部分:低频信息和高频信息。低频信息是变化缓慢的部分，是信号的框架，占全部信息的大部分;高频信息是变化迅速的部分，它反映的是信号的细节信息，占全部信息的小部分。总之，由于在小波分解下，不同的尺度具有不同的时间和频率分辨率，因而得用小波分解可以将信号的不同频率区间所包含信号分离开来，从而达到识别出震相目标。

2 模拟信号仿真实验

为了验证前面所讲述的信号初至及震相识别方法的有效性，通过对模拟信号进行处理，识别出相应的初至位置和震相特性。识别的结果与真实的信号特性进行比较，验证识别的准确性。

通过5个正弦波:

图1 模拟信号Fig.1 Simulation Signal

图2 模拟信号小波包分解初动识别Fig.2 wavelet packet decomposition of simulation signal

采用对数能量熵优化法找到分解的最优基，图2 是对信号进行db6 小波包2 层分解结果，(2，0)、(2，1)、(2，2)、(2，3)分别为LL，LH，HL，HH 分解结果。从图2 可以看出，每一个新的信号到达时，都会有一个异常高频产生。识别的结果和信号的真实初动位置基本相同。信号的时频分布特征不同，初值位置检测效果最佳的分解尺度也将不同。

图3 是应用db5 小波对模拟信号进行5 层分解。分解的细节信号分别为图中的d1 到d5 所显示的信号。从图中可以看出，经过小波变换分解之后，可以容易的看出不同频率的信号所出现在的相应位置。d1 层细节信号显示的是信号中最高频率的信号，所在的区间为300 点之后;d2 层细节信号显示的是信号中较高频率的信号，所在的区间为200 点之后;d3 层细节信号显示的是信号中中频信号，所在的区间为100 点之后。所以我们可以从图中看出信号的频率分布情况，从而识别出他们相应的震相。d4、d5 层是信号分解的相对低频信号，对初值检测意义不大。将这两个识别的结果综合起来，就可以识别出初动位置相应的初动震相。

图3 模拟信号小波变换的各层细节信号Fig.3 Wavelet transformation detail signal of simulation signal

3 实际地震信号初震及震相识别

通过前面模拟信号的识别结果发现，应用小波包变换结合小波变换识别信号的初震和震相是比较有效的震相识别方法。应用该方法对汶川地震余震的实测天然地震信号(图4)进行初震及震相识别。

由于地震信号成分比较复杂，记录过程中还会带有很多的噪音，所以对地震信号的初震识别时要结合几个尺度的系数能量分布情况进行整体分析。从图5 可以看出，地震信号的第一个初动位置坐标为675 那个点的位置，对应的时间为13.5 s;第二个初动位置坐标为1 249 那个点的位置，对应的时间为24.98 s;第三个初动位置坐标为2810 那个点的位置，对应的时间为56.2 s。然后再用小波变换对信号进行分解，分离出它的不同频率成分，达到震相识别的目的。

图4 汶川地震南北向地震记录Fig.4 Seismic record of WenChuan earthquake

图5 实测地震信号小波包分解初至识别Fig.5 Wavelet packet decomposition first arrival recognition of actual measurement

图6 地震信号小波变换的各层细节信号Fig.6 Wavelet transformation detail signal of seismic signal

图6 是地震信号经过db5 小波变换5 层分解的细节信号分布图。d1 为信号中最高频率的分布情况，d5 和a5 是地震信号中频率较低的那部分分布情况。可以知道先到达的是高频成分的P 波，其次是中频部分的S 波，然后是低频部分的面波。结合两个分析的结果，可以得到P 波的初至时间为13.5 s;S 波的初至时间为24.98 s;面波的初至时间为56.2 s。

4 结论

本文先用小波包变换确定信号的初动位置，再用小波变换分解信号，分离出不同频率信号以根据频率确定震相，两者结合确定不同震相的初至时间。该方法可以综合利用地震信号信息，对地震监测资料的震相识别及其初至时间提取比单一分析法有更好的结果。

刘希强，周惠兰.2002.高斯线调频小波变换及其在地震震相识别中的应用［J］.地震学报，24(6):607-616.

刘希强，周蕙兰，郑治真.1998. 基于小波包变换的弱震相识别方法［J］.地震学报，20(4):373-380.

强淋，刘贵忠.1997.阵列声波全波列测井信号波至提取的小波变换方法［J］.石油物探，36(2):55-61.

秦前清，杨宗凯.1995.实用小波分析［M］.西安:西安电子科技大学出版社.

冉启文.2001.小波分析与分数傅里叶变换理论及应用［M］. 哈尔滨:哈尔滨工业出版社.

王大凯，彭进业.2006.小波分析及其在信号处理中的应用［M］. 北京:电子工业出版社.

杨配新，邓存华，刘希强，等.2004.数字化地震记录震相自动识别的方法研究［J］.地震研究，27(4):308-313.

郑治真，沈萍，等.2001.小波变换及其MATLAB 工具的应用［M］.北京:地震出版社.

周彦文，刘希强.2007.初至震相自动识别方法研究与发展趋势［J］.华北地震科学，25(4):18-22.

Kanwaldip S Anant ，Farid U. Dowla.1997.Wavelet Transform Methods for Phase Identification in Three-Component Seismograms［J］.Bulletin of the Seismological Society of America，87(6):1598-1612.

Zhikun Hou，Adriana Hera，Abhijeet Shinde. 2006. Wavelet-Based Structural Health Monitoring of Earthquake Excited Structures［J］.Computer-Aided Civil and Infrastructure Engineering ，21(4):268-279.