低空遥感影像全自动快速匹配方法研究

何海清， 刘 波， 谭术升

(东华理工大学测绘工程学院，江西 南昌 330013)

以无人机作为平台的低空数字摄影测量具有高分辨率、高时效性、高机动性、低成本等优势，是卫星遥感和传统有人机航空摄影测量的重要补充，对于资源环境调查、城市规划、灾害应急监测等具有很强的实用性。然而，无人机低空数字摄影测量也存在一些技术难点亟待解决。无人机飞行过程中易受气流等外力的影响，而且由于其自身载荷等限制，无法搭载一些高精度的定位定姿设备，难于准确记录瞬间摄影姿态，给内业数据处理带来较大负担。同时，无人机获取的影像具有像幅数多、数据量大等特点。因此，高自动化内业影像数据快速处理对于发挥无人机优势有着重要的意义。其中，无人机影像匹配的精确度、稳健性和效率直接关系到无人机低空数字摄影测量自动化程度。迄今为止，国内外学者对影像匹配进行了广泛和深入的研究，最具代表性的有基于灰度的匹配算法、最小二乘影像匹配、SIFT 匹配算法等。其中，SIFT 算法是一种稳健性很高的匹配算法，能够提供稳定的尺度、旋转及平移不变特征(王佩军等，2010)，对于无人机影像匹配研究具有代表性的是利用SIFT 算法进行无人机影像自动特征提取与匹配(Lingua et al.，2009)、利用SIFT 算法进行无人机摄影测量影像匹配研究(Cesetti et al.，2011)、粗匹配加分块SIFT 无人机影像匹配方法(何孝莹等，2011)等。目前，大多数无人机影像匹配算法难兼顾精确性及高效性，对于时效性要求较高的无人机低空摄影测量仍显不足。

本文针对SIFT 匹配在无人机影像中匹配效率较低等问题，利用Harris 提取无人机影像角点，简化SIFT 描述子，并记录每一角点描述子Freeman 形状链与各方向梯度累加值，根据累加值大小进行排序，比对像对间累加值相近的一定范围内的角点，具有Freeman 链码最长公共子串的对应角点视为初始匹配点，然后通过RANSAC 剔除粗差，得到精确的匹配点，在精确度和效率方面取得了较好的效果，具有一定的实用性。

1 角点检测算法

为了减少特征点提取计算量，本文采用简单高效、应用较为广泛的Harris 角点检测算法(Schmid et al.，2000;晏启明等，2013)，该算法利用梯度算子计算像素点在任意方向上的灰度变化，通过角点响应函数值CRF(Corner Response Function)和阈值确定角点。CRF 表达式为

式中，k 为常数项，其取值范围为0.04 ～0.06，det M为M 矩阵的行列式，traceM 为矩阵M 的迹，M 为

式中，G 表示高斯滤波，Ix、Iy分别表示图像点x 方向和y 方向上的一阶灰度梯度。

2 简化SIFT 的描述子匹配策略

Lowe(1999)提出了一种尺度、旋转和平移不变的SIFT(Scale Invariant Feature Transform)特征提取算法，该算法表述角点具有光照和视点变化的不变性，但在特征向量提取和描述子计算效率较低(王佩军等，2010;贺亮等，2011)。本文根据SIFT 算法中特征描述方法，通过简化的描述子对角点进行描述，以梯度累加值与Freeman 描述子形状链码作为相似性度量，实现角点粗匹配。然后，通过RANSAC 算法提纯匹配点。

2.1 简化SIFT 描述子

为使算子具有旋转不变性，利用邻域一定范围内像素的梯度大小及方向，确定每个角点最大梯度方向，像素I(x，y)的梯度m(x，y)和方向θ(x，y)表达式为

创建角点梯度直方图，并设定范围为0° ～360°，每10°为1 柱，共36个柱，对角点邻域像素梯度进行统计。利用高斯算法对像素梯度大小进行加权，距离角点越远，权重越小。根据每一邻域像素点梯度方向，把梯度加权值归入对应直方图柱内。最后，选择直方图的峰值代表该角点的主方向。为确保角点旋转不变性，图像坐标轴旋转到角点的主方向。常用的SIFT 描述向量取16 ×16 大小的邻域窗口，并划分为16个4 ×4 子块，统计每一子块8个梯度方向归一化的梯度值来描述特征点，关键点特征向量见图1。

本文方法仍取常用方法相同的邻域窗口，但只统计角点18个方向上的梯度大小来描述角点，降低了描述子维数，从而也降低了描述子的复杂性，简化了描述子计算过程，该描述子见图2。

图1 关键点特征向量Fig.1 The feature vector of key point

图2 简化的描述子Fig.2 The simplified descriptor

为强化描述子的稳健性，在表征简化描述子梯度大小和方向的同时，引入描述子Freeman(Freeman，1961)形状特征度量的链码来进一步约束匹配，从而使描述子更加完备，以达到降低SIFT 描述子复杂度而不失稳健性，描述子形状见图3。Freeman 形状编码规则见图4，按逆时针方向进行编码，360°空间以每45°作为步长，码值分别为01234567，简化SIFT 描述子编码规则为

式中，a 为边长矢量方向。见图5，该角点Freeman形状链码为31435647506171720。

图3 描述子外围形状Fig.3 The shape of descriptor

图4 Freeman 编码规则Fig.4 Freeman code

采用两角点Freeman 链码串具有最长公共子串来表征两角点形状相似性。对需匹配的其中一幅影像的每个角点按照其描述子18个方向的归一化梯度值之和排序，另一影像中角点搜寻对应匹配影像归一化梯度值之和相近值的一定区间(表示梯度范围阈值)内的角点，通过Freeman 形状链码来比对这些角点来确定初始同名点，可减少欧式距离等相似性度量的重复搜索负担，实现角点粗匹配，对于同时满足Freeman 链码具有最长公共子串和角点归一化梯度值最接近的视为初始匹配点。

2.2 RANSAC 剔除粗差

上节角点初匹配时，可能存在一些误匹配点，本文采用随机采样一致性RANSAC(Random Sample Consensus)算法(Fischler et al.，1981)剔除误匹配点和粗差，实现角点精匹配。RANSAC 算法假设一组包含粗差的观测量分为内点和外点，通过迭代方式筛选内点来估计数学模型的参数，实现剔除不准确匹配点的方法。

一般情况下，无人机低空数字摄影测量过程中，影像是通过焦距固定的相机来获取，以透视投影变换单应矩阵作为估计模型，其变换关系为

单应矩阵中含有8个未知数，通过不存在3 点共线的4 对匹配点即可解出H。重复N 次从粗匹配点集中随机抽取4 对粗匹配点，计算其单应矩阵H，设p 为采样得到的匹配点为内点的概率，pi为每次从粗匹配点集中选取一个内点的概率，采样次数N然后，利用矩阵变换每一粗匹配点，并计算变换后与对应匹配点的欧式距离d 为

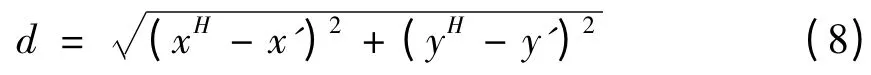
式中，(xH，yH)为(x，y)经过单应矩阵H 变换后的坐标，T 为给定阈值，当满足d ＜T 时，该粗匹配点为内点。最后，N 迭代抽样后得到的内定视为精匹配点。

3 实验结果及分析

为了验证本文方法在影像匹配效率上的改进，采用一条航带10 幅分辨率为3 744 ×5 616 的无人机影像进行实验。

经多次实验，统计少于12个方向直方图的SIFT 描述子误匹配点较多，匹配结果不稳定，易出现匹配失败。同时，实验表明仅简化描述子利用欧式距离作为相似性度量，而未引入Freeman 形状链码进行二度约束，匹配结果也可能不稳定，有可能导致匹配失败。

为此，实验通过比对角点12 ～36 步长为1 的各个方向上匹配方法所耗时来寻找最佳统计直方图方向数，实验表明方向数越少SIFT 粗匹配时间越少但误匹配点越多，且RANSAC 剔除误匹配点所耗时间越多;随着方向数增多，粗匹配时间增加但误匹配点减少，RANSAC 剔除误匹配点所耗时间也减少，各方向描述子耗时统计及其多项式拟合曲线关系，见图6。显然，统计18个方向直方图的简化描述子耗时最少，其中两个像对角点检测及匹配结果见图7，在图7(a)、(b)中匹配点数分别为87 和126，○标示匹配点、连线标示对应匹配点。

一条航带各个像对SIFT 与本文改进的Harris-SIFT 粗匹配与粗差剔除等各阶段在同一硬件环境下所耗时间见表1，可见本文改进的匹配方法所耗时仅为SIFT 方法的1/7 倍，大幅提高了影像匹配效率。

4 结论

图6 各方向简化SIFT 耗时关系Fig.6 The relationship of time consuming and simplified SIFT with different orientation

无人机低空数字摄影测量影像全自动快速匹配对于应急调查、应急决策等应用是一项非常迫切的工作，本文利用Harris 与SIFT 特征点描述子结合，并引入描述子Freeman 链码表征特征点形状来进行相似性度量，从而实现无人机影像全自动快速匹配。通过一条航带的无人机影像进行匹配实验，表明本文方法可得到稳健的匹配点，且相对于SIFT 算法可大幅提高无人机影像匹配效率，所耗时间仅为SIFT 匹配的1/7，对于提高无人机影像处理时效性具有一定的实用价值。

图7 匹配效果Fig.7 The matching results

表1 SIFT 与本文方法匹配所耗时间统计Table 1 Time consuming of SIFT and improved SIFT matching s

何孝莹，岳建伟，张栩然.2011.基于SIFT 算法的无人机影像快速匹配［J］.计算机工程，37(7):216-218.

贺亮，刘荣，吕开云.2011.一种基于种子生长的匹配算法［J］. 东华理工大学学报:自然科学版，34(4):379-383.

王佩军，徐亚明.2010.摄影测量学［M］.武汉:武汉大学出版社.

晏启明，程朋根.2013.CIPS 空三加密技术与应用［J］. 东华理工大学学报:自然科学版，36(2):224-227.

Cesetti A，Frontoni E，Mancini A. 2011. A visual global positioning system for unmanned aerial vehicles used in photogrammetric applications［J］. Journal of Intelligent ＆ Robotic Systems，61(4):157-168.

Fischler M A，Bolles R C. 1981. Random Sample Consensus:A paradigm for model fitting with applications to image analysis and automated cartography［J］. Communications of the ACM，24(6):381-395.

Freeman H. 1961. On the encoding of arbitrary geometric configurations［J］. IRE Transactions on Electronic Computers，10:260-268.

Lingua A，Marenchino D，Nex F. 2009. Performance analysis of the SIFT operator for automatic feature extraction and matching in photogrammetric applications［J］. Sensors，9(5):3745-3766.

Lowe D G. 1999. Object recognition from local scale-invariant features［C］. Proceedings of the IEEE International Conference on Computer Vision，1150-1157.

Schmid C，Mohr R，Bauckhage C. 2000. Evaluation of interesting point detectors［J］. International Journal of Computer Vision，37(2):151-172.