瞬变电磁2.5维有限元正演的程序实现过程
梁建刚, 瓮晶波
(1.中国地质调查局天津地质调查中心,天津 300170;2.中南大学,湖南 长沙 410083)
2.5 维人工源时间域电磁场数值模拟(正演)问题近些年发展很快(Leppin,1992;Everett et al.,1993;Mitsuhata,2000;Meng et al.,1999),这是因为较之于纯二维的数值模拟,2.5 维方法考虑到了场源的三维性质,更贴近于野外实际地质情况,另一方面,较之真正的三维方法,2.5 维方法大大减少了计算量,得以在普通性能的微机上顺利实现(王华军等,2003;熊彬等,2006;熊彬,2005;金建铭,1998)。
时间域的电磁场问题,实际上是一个空间加时间的四维边值问题。
瞬变电磁2.5 维有限单元法正演二次场算法中以均匀大地或层状大地的瞬变电磁响应为一次场,其间异常体的响应为二次场(纯异常),二次场的场源为异常体处的一次场,从而避免了计算阶跃脉冲的响应。其公式推导及实现思路是:首先对电磁场作拉氏变换,将时间域问题变成拉氏域(或称频率s 域)中的问题,实现降维(消除时间变量t),考虑到二维地电条件下ε、μ 和σ 与坐标轴y 无关,沿y 轴对电磁场作傅氏变换,转换成(s,m)域中的边值问题。在(s,m)域中实现电磁场的求解,然后再经拉氏逆变换、傅氏逆变换后重新回到时间空间域。
编写程序的过程中,一次场的求取和傅氏逆变换两次用到余弦变换,拉氏逆变换则用普遍接受的G-S 变换得以实现。线性方程则在证明刚度矩阵对阵性的基础上,经LDLT实现。
1 (s,m)域中求解
1.1 变分问题
用e,h 表示(s,m)域中的电场和磁场,再经过边界问题的推导,得到瞬变电磁2.5 维正演等价的泛函分析(王华军等,2003):
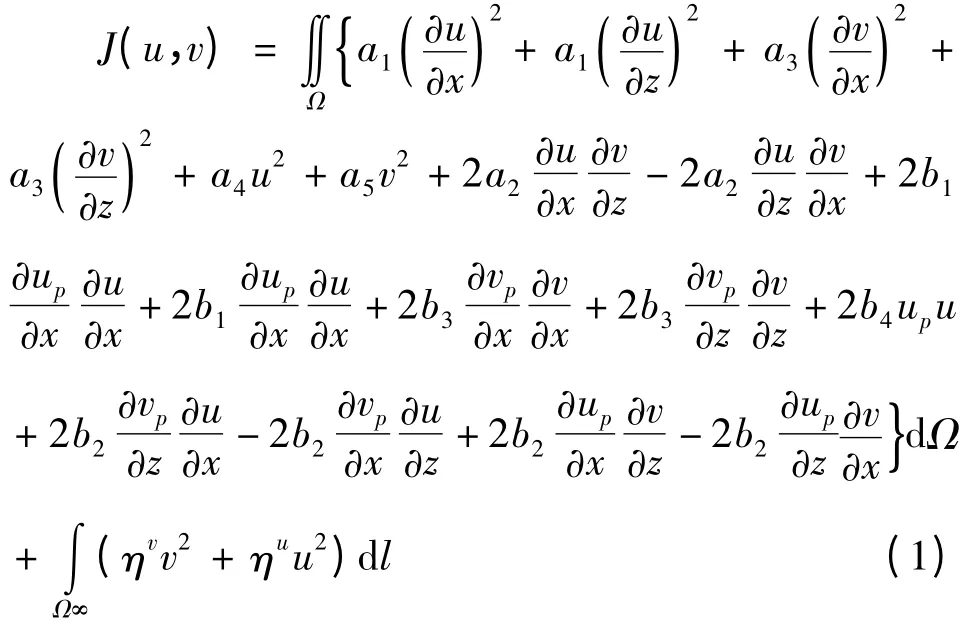
式中,up= ep,y,vp= - ihp,yu = es,y,v = hs,y,=

e,y,hp,y,es,y,hs,y分别为拉式傅氏(s,m)域沿走向方向的一次场,二次场分量,k 为介质的传播系数,m 为沿走向的傅氏域波数,s 为拉式空间变量,ε为介质的介电常数,μ 为磁导率,σ、δσ 为介质的电导率及异常电导率(异常体与均匀介质电导率之差),ηu、ηv为区域边界系数,i 为复数单位。
1.2 有限单元法
用有限单元法求解变分问题,将(1)式离散化后变为:

1.3 矩形剖分条件下单元分析:
单元积分1:

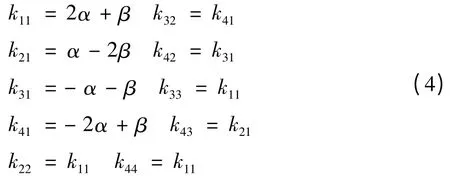
单元积分2:

单元积分3:
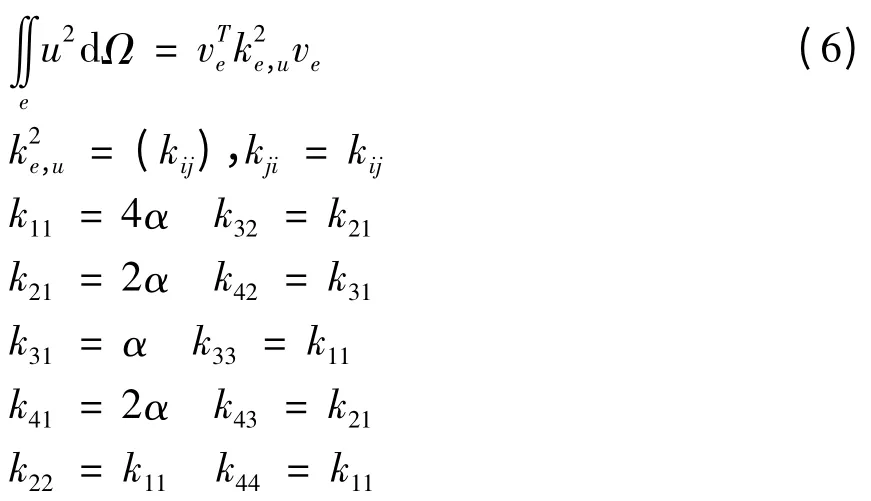
单元积分4:

单元积分5:

为了使总的刚度矩阵对称,需要对反对称矩阵做适当线性变换:

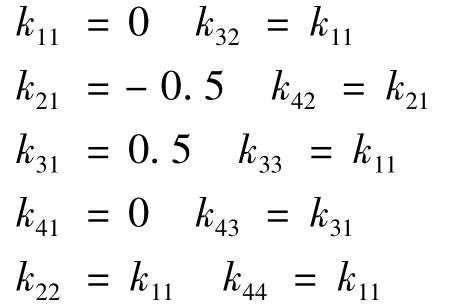
单元积分6:
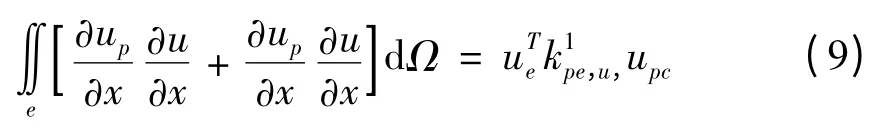
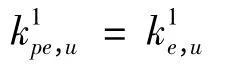
单元积分7:
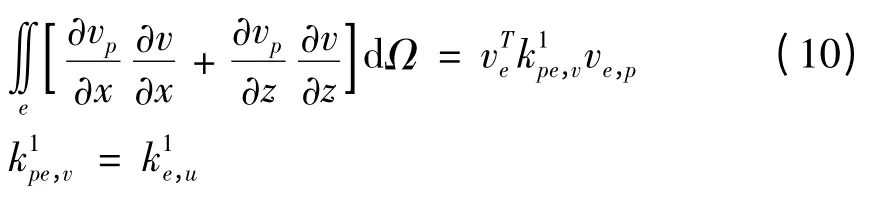
单元积分8:
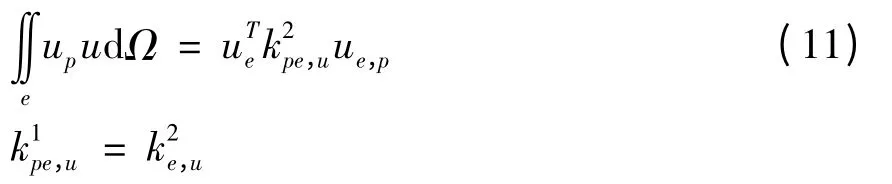
单元积分9:

单元积分10:
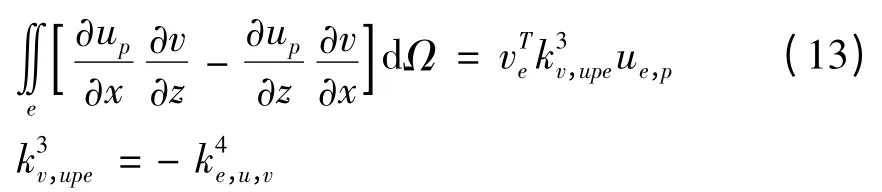
单元积分11:
1.4 总体合成
对上述求得的子刚度矩阵先由4 ×4 的矩阵扩展为8 ×8 的矩阵,然后合成总体矩阵为:
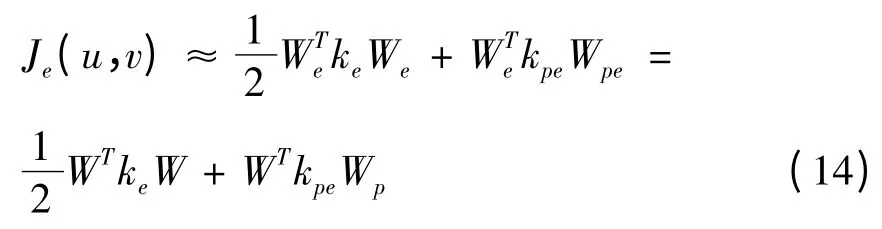
再者,各单元扩展后的列向量W,Wp是相同的,所以各单元积分相加时只需将ke和kpe相加,即:
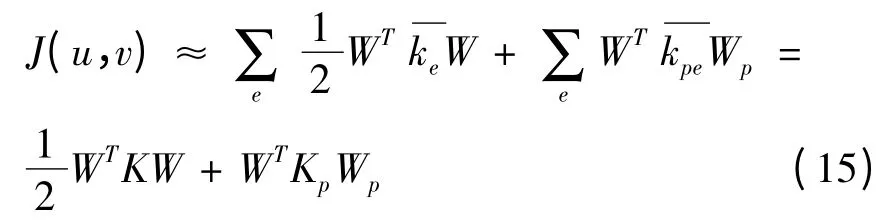
1.5 求变分
对(15)式求变分,并令其为零,δJ(u,v)=δWTKW + WTKδW + δWTKpWp= 0 考虑到K 的对称性,有δWTKW = WTKδW,并且δWT≠0,故而有

在(16)式中,K、Kp由单元分析求得,Wp是异常体处的一次电磁场,由解析式求得。求解方程组可得到W,即二次电场、磁场分量。
这样就把变分问题转化为求解线性方程组,这是有限单元法的精髓。
1.6 线性方程组的求解
经验证,所求得的线性方程组的矩阵是对称的稀疏矩阵。求解这样的方程组时,若完全套用一般格式,则不仅要存贮大量的零元素,而且还要让它们参加运算,在存贮量、计算量方面定会造成巨大浪费。本文按照徐世浙(1994)中的做法,等带宽存贮稀疏刚度矩阵,并用书中所附LDLT程序进行求解(在横向剖分40个单元,纵向剖分30个单元的情况下半带宽为66)。
2 拉氏逆变换、傅氏逆变换及其关键点
经上述有限元计算求解出域的电磁场值,必须进行拉氏逆变换、傅氏逆变换才能转换成时间空间域的电磁场值。
2.1 拉氏逆变换
考虑到Gaver-Stehfest 变换是纯实数运算,而且只需对较少的拉氏变量作计算,是一种计算较快的算法,本文直接用它来作拉氏逆变换,实现频域到时域的转换(罗延钟等,2000;熊彬,2005)。
设拉氏空间的像函数为F(s),实空间的像原函数为f(t)则:
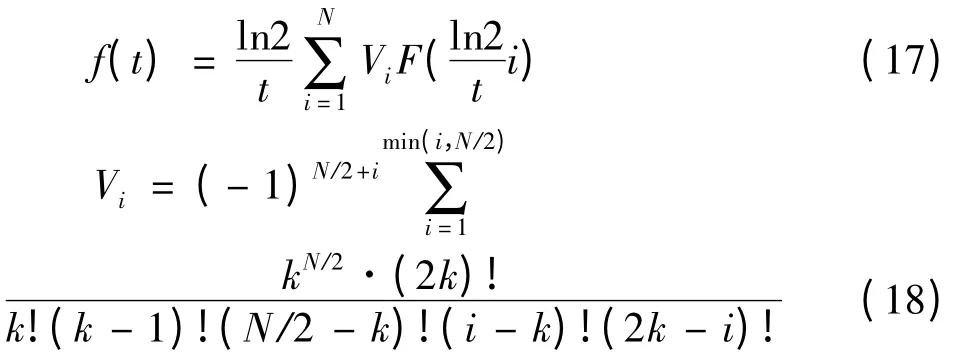
其中N 是取决于计算机位数的正整数。本文中取N= 12。
2.2 傅氏逆变换及一次场计算
由于拉氏逆变换算法对精度要求高,必须先做拉氏逆变换再做傅氏逆变换(图1)。傅氏逆变换主要完成从波速域向三维(x,y,z)空间的转换,计算公式为(肖明顺,2008;昌彦君等,1995):
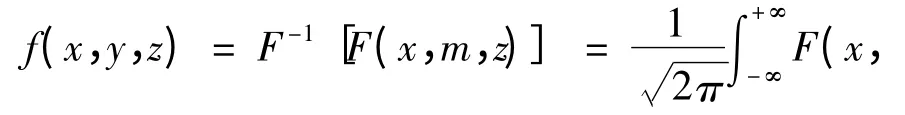

在瞬变电磁2.5 维正演中,上式有三个显著的意义:
(1)当y ≠0 时,即计算非主剖面电磁场,也就是旁测剖面的电磁场值,这是2.5 维算法区别于纯2 维算法的显著特征之一。
(2)当z >0 时,即计算地下介质中的电磁场值。这为井中瞬变电磁的正演提供了途经。
(3)上式中的参数对应着电磁法中的收发矩参数,对于瞬变电磁法的中心回线装置,收发矩x= 0。
因此,完整的2.5 维瞬变电磁正演中的傅氏逆变换应该囊括以上三种情况。本文中关心的主剖面、地表上、零收发距的瞬变电磁场的参数为:x =0,y = 0,z = 0。
考虑到位于主剖面的回线源所产生的垂向磁分量在空间域中相对于y 具有偶对称性,对回线中心的主剖面上y = 0 的hz,s作傅氏逆变换时,正弦项为零,余弦项为1,积分内项变为核函数本身。
这样(19)式就变为:
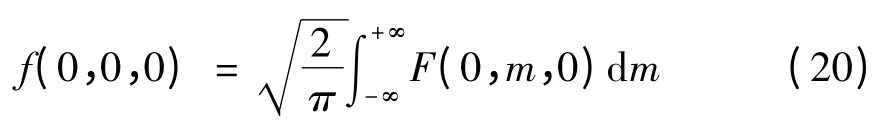
加之在进行有限元计算前,一次场的求解过程中,对给定的m 和发射回线的半边长b,sin(mb)为常量,而傅氏逆变换又是在相同波数
序列中进行的,所以在求解一次场ey,hy时不计算sin(mb),而把它放在傅氏逆变换中。这样原本偶对称的hz,s貌似变成了奇对称。经这么处理,瞬变电磁2.5 维有限元正演中的傅氏逆变换就转化为正弦变换。
(20)式进一步变为:
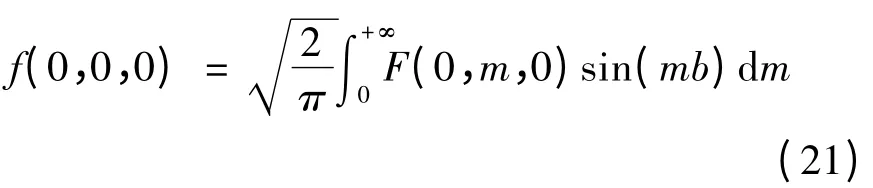
编程时直接使用(21)式,用正弦变换实现傅氏逆变换。
而二次场计算所涉及的一次场计算应用公式文中直接用王华军等(2003)的计算公式:
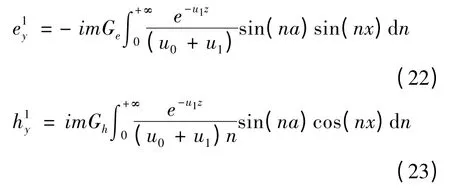
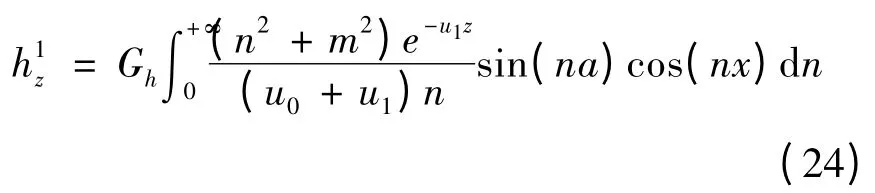
其中
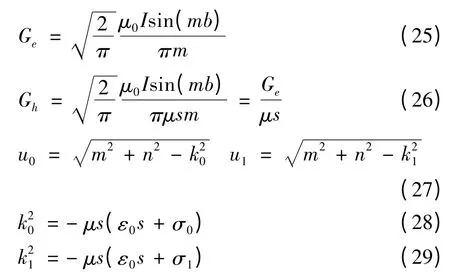
(22)、(23)、(24)三式均含有正弦或余弦高振荡函数,用正余弦变换进行求解(王华军,2004)。
至此,程序实现中应用到两次正弦变换(一次场求取与傅氏逆变换)。
2.3 波数选择
本文中傅氏域波数的选择,是从两个方面考虑的:一方面,有限元计算时选择的波数跟进行傅氏逆变换时的波数是一样的,本文中的傅氏逆变换最后转化为正弦变换;另一方面,根据Hz 随波数变化情况,即不同波数范围对积分的贡献程度。综合上述两个方面,程序实现时波数范围的选择方案为,21个波数指数等间隔取为10-8~1 范围内正弦变换的节点enΔ/k,在进行傅氏逆变换之前用三次样条插值法指数等间隔插值成161个波数及场值。
3 程序流程图
实现2 维模型多测点剖面的瞬变电磁2.5 维有限单元法正演需要有四重循环,从里层到外层分别为:①测点;②s(拉氏逆变换);③m(波数或傅氏逆变换);④t(采样时间)。具体的程序流程如图1。
4 正演结果
4.1 模型1(低阻)
为了验证2.5 维程序的正确性及精度,用2.5维程序计算了有解析解的一维模型。

图1 程序流程图Fig.1 The flow chart of procedure
模型1 的参数为:ρ1= 100 Ω·m,h1= 100 m,ρ2= 20 Ω·m,h2= 50 m,ρ3= 100 Ω·m。中心回线装置的发射回线边长。
从图2 可以看出,纯异常(二次场)有限元解与解析解曲线形态完全相同,但幅值有一定的误差。其中在异常的峰值点相对误差为5.49%。
4.2 模型2
模型的参数为:ρ1= 100 Ω·m,h1= 100 m,ρ2= 20 Ω·m,h2= 50 m,ρ3= 100 Ω·m。中心回线装置的发射回线边长。
从图3 可以看出,纯异常(二次场)有限元解与解析解曲线形态完全相同,但幅值有一定的误差,且在时间轴方向,有限元解与解析解之间有大约一个采样间隔的时间位移,两条曲线的其中在异常的峰值点相对误差为0.7%。
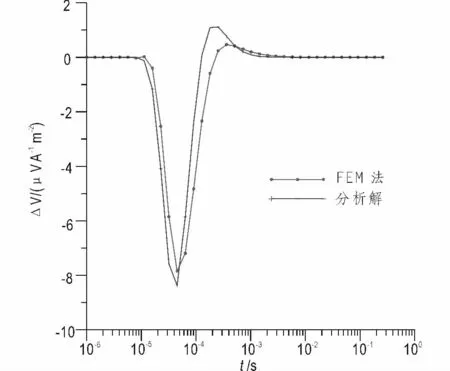
图2 模型1 二次场比较图Fig.2 The second field compare chart of model 1
在 Inter(R)core(TM)i5-2540 M CPU,2.60 GHz,4.00G 内存的笔记本电脑上,剖分30 ×40个单元格,异常体5 ×40个单元格,计算16个波数,41个时间需要602 s。
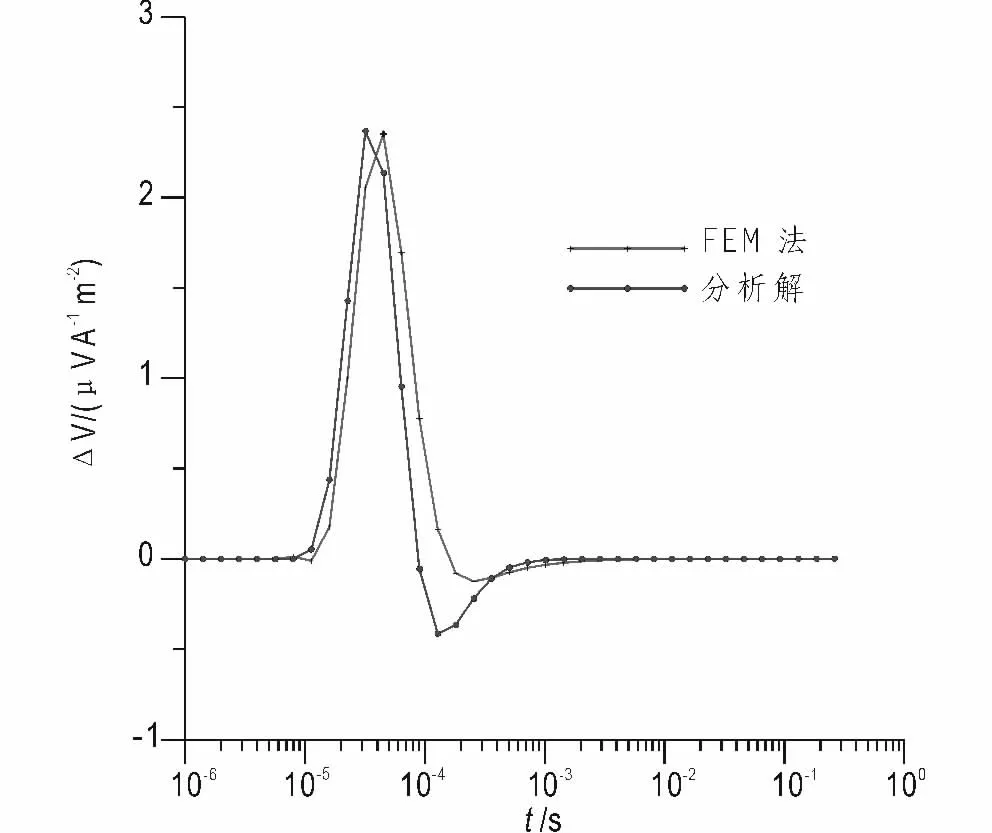
图3 模型2 二次场比较图Fig.3 The second field compare chart of model 2
综合模型1 和模型2,可以看到有限元解与解析解曲线形态完全相同,在时间轴方向均有一定的时间位移(有限元解滞后于解析解),经分析认为是在两种介质的界面,解析解可以实现瞬间过渡,而有限元则对应于两个不同物性特征的剖分单元,可以在单元剖分时在界面处剖分加密,但永远无法实现瞬间过渡。基于同样原因,在纯二次异常的晚期反向异常,有限元解滞后于解析解,且幅值相对较小。
4.3 模型3
模型的参数为:均匀半空间ρ1= 100 Ω·m,异常体h1= 100 m,厚度为10 m,宽100 m(x 为450 ~550 m,中心位置x =500 m),ρ2=10 Ω·m(模拟采空区,如图4)。中心回线装置的发射回线边长2b =50 m,测量范围x 为350 ~650 m。

图4 模型3 地电断面示意图Fig.4 The geological-electricity sketch map of model 3
图5 为异常中心左侧11个测点的二次场的场值,从图上可以看到,随着测量点由远到近逐渐接近异常体中心,二次场的异常范围逐渐变小,二次场峰值逐渐变大,峰值对应的时间逐渐变小(其中异常中心位置二次场极值出现在32 μs)。这一现象可以用波场传播的角度解释,随着由远到近电磁波遇到异常体的距离也逐渐减小,响应时间逐渐提前,异常效应逐渐变大。
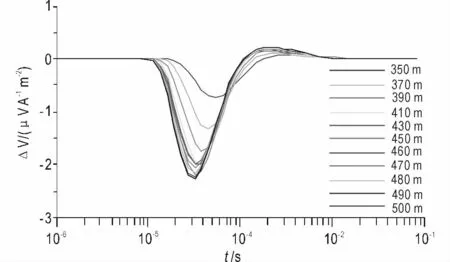
图5 各测点二次场图Fig.5 The second field chart of different measuring points
图6 为21个测点的总场的衰减曲线。可以参照图5 解释图6 中的各种现象,从上图可以看到,高阻围岩条件下的低阻异常体模型,总场衰减曲线大致经过如下三个阶段:
(1)二次场异常在早期相对一次场(总场)较小,500 m 处(异常体中心位置)纯二次场在32 μs时早期假异常达到最大,但这时二次场相对一次场很小,在总场曲线上几乎没有反应。
(2)181 ~512 μs 看到的明显的正异常。
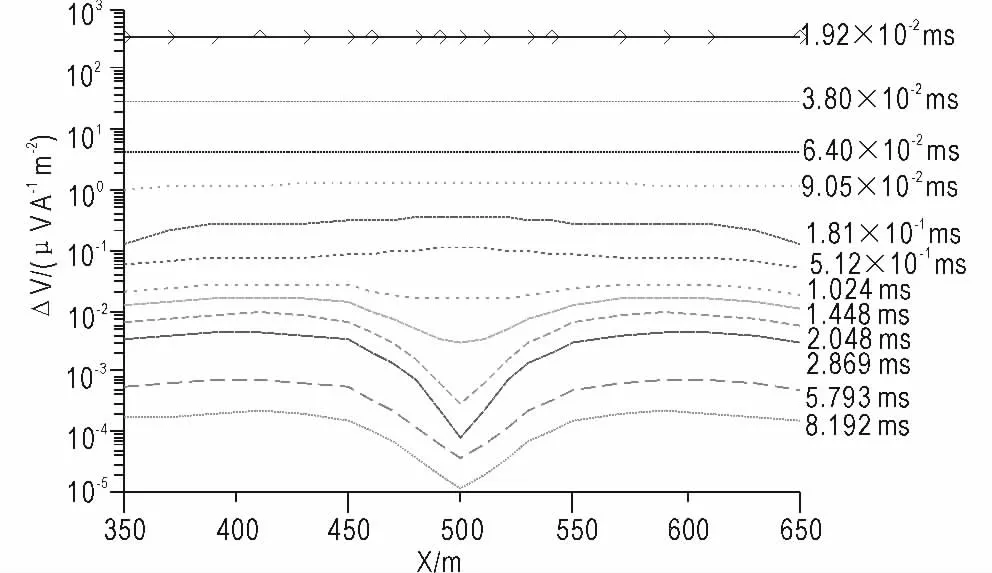
图6 测量剖面总场衰减曲线图Fig.6 The total field decline chart of measuring profile
(3)1.024 ms 之后的貌似与一维正演纵向(时间)特征相矛盾的反常现象。为此加大测量范围并提取了8.192 ms 时刻的二次场曲线。
二次场在8.192 ms时刻均为正值,与181 μs时刻方向相同,之所以出现图5 中的现象,是要因为图中没有画出一次场的水平,而由于地电断面横向不均匀性,二次场在异常体中心位置较小,其最大值出现在距离异常中心410 m 和590 m 处。这一现象是1 维正演中无法看到了的,是烟圈效应的体现(牛之琏,2007)。
另外曲线呈现出较好的对称性,是对熊彬等(2006)的修正。
从图7 可以看到模型3 地电条件下,8.192 ms时异常场的数量级已经到pV,是否能够有效探测跟仪器的灵敏度、地质噪声等密切相关。
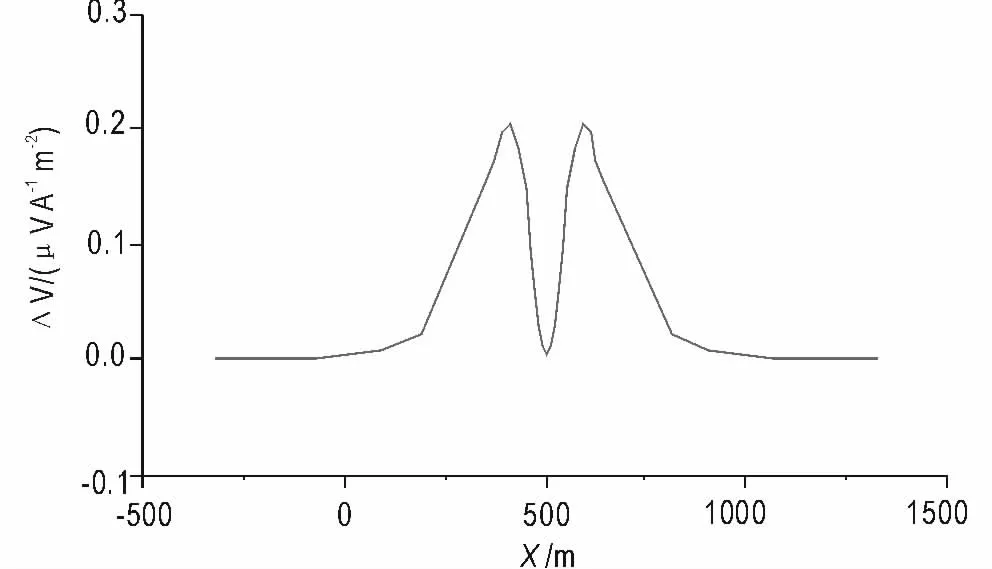
图7 8.192 ms 二次场剖面图Fig.7 The second field profile at 8.192 ms
5 结论
(1)本文以前人推导的2.5 维瞬变电磁泛函公式为基础,进一步梳理了矩形剖分下的有限元正演过程,对程序实现过程中的一次场求取、傅氏逆变换、拉氏逆变换以及刚度矩阵对称性及其解法进行了详细的阐述,并运用自己编写的程序计算了三个模型。
(2)瞬变电磁2.5 维正演较一维正演更贴近客观事实,尤其是针对煤田巷道等模型,模型计算出的响应可以部分解释瞬变电磁波场的眼圈效应;相对三维正演又节约时间。
(3)瞬变电磁2.5 维正演在计算精度、运算速度上还有待进一步提高。在精度提高的情况下,可以计算地质体的电场响应,并与地质噪声、仪器噪声、仪器灵敏度相比较,从而实现瞬变电磁勘察2D地质体的可行性分析。
昌彦君,张桂青.1995.电磁场从频率域转换到时间域的几种算法比较[J].物探化探计算技术,17(3):25-29.
金建铭. 1998.电磁场有限元方法[M]. 西安:西安电子科学出版社:1-34.
罗延钟,昌彦君. 2000.G-S 变换的快速算法[J].地球物理学报,43(5):684.
牛之琏.2007.时间域电磁法原理[M]. 长沙:中南大学出版社:37-48.
王华军,罗延钟. 2003.中心回线瞬变电磁法2.5 维有限单元算法[J].地球物理学报,46(6):855-862.
王华军. 2004. 正余弦变换的数值滤波算法[J]. 工程地球物理学报,1(4):329-335.
肖明顺. 2008. 带地形的瞬变电磁2. 5 维有限元数值模拟研究[D].武汉:中国地质大学:1-50.
熊彬,罗延钟. 2006.电导率分块均匀的瞬变电磁2.5 维有限元数值模拟[J].地球物理学报,49(2):590-597.
熊彬. 2005.关于瞬变电磁法2.5 维正演中的几个问题[J]. 物探化探计算技术,28(2):124-128.
徐世浙.1994 地球物理中的有限单元法[M].北京:科学出版社:1-157.
Everett M E,Edwards R N. 1993. Transient marine electromagnetics:the 2.5D forward problem[J]. Geophys.Int,113(3):545-561.
Leppin M. 1992.Electromagnetic modeling of 3D sources over 2D inhomogeneties in the time domain[J]. Geophysics,57(2):994-1003.
Meng YL,Li W D,Zhdanov M,et al. 1999.2.5-D eletromagnetic forward modeling in the time and frequency domains using the finite element method[A]//SEG’69 annual Meeting Expanded Abstracts,Tulsa:Society of Exploration Geophysicists:1-7.
Mitsuhata Y J. 2000. 2-D electromagnetic modeling by finite element method with a dipole sourceand topography[J]. Geophysics,65(4):465-475.

