马尾松人工纯林全林整体生物量模型的构建

郭文清， 李桂珍， 刘 沙， 谭刚毅

(1.湖南省林业科学院， 湖南 长沙 410004； 2.怀化市林业局， 湖南 怀化 418000；3.湖南省林业厅， 湖南 长沙 410007； 4.攸县林业局， 湖南 攸县 412300)

马尾松人工纯林全林整体生物量模型的构建

郭文清1， 李桂珍2， 刘 沙3， 谭刚毅4

(1.湖南省林业科学院， 湖南 长沙 410004； 2.怀化市林业局， 湖南 怀化 418000；3.湖南省林业厅， 湖南 长沙 410007； 4.攸县林业局， 湖南 攸县 412300)

以湖南省会同县马尾松纯林为研究对象，采用两阶段度量误差模型法对马尾松林分蓄积量与各组分生物量回归模型和全林整体生长模型进行融合，并对模型的参数进行重新估计，得到马尾松纯林全林整体生物量模型，经检验模型精度较高，适用性强。

全林整体生物量模型； 两阶段度量误差模型； 马尾松

传统的测定林分生物量的方法均需繁重的野外工作，而且由小面积的测定结果推广到大面积的森林也相当困难。有学者研究表明，林分蓄积量和生物量的高低，受立地条件、林分年龄和人为干扰影响较大，可以认为林分生物量W是地位指数L、密度指数S、形高fH和林分年龄t的函数[1-2]。本研究在李桂珍、郭文清等[3]建立的马尾松全林整体生长模型的基础上，结合张翼、郭文清等[4]研建的林分蓄积量与各组分生物量相关关系模型，采用两阶段度量误差模型方法[1，5-7]融合模型进行参数的拟合以构建马尾松全林整体生物量模型。

1 研究区概况

会同县隶属于湖南省怀化市，地处云贵高原东缘斜坡，雪峰山脉的西南，全境属中、低山区，境内属亚热带湿润季风气候，主要特点为四季分明，降雨适中，夏无酷热，冬少严寒。年平均气温16.6 ℃，1月平均气温4.9 ℃，极低气温为-8.5 ℃。7月平均气温27.3 ℃，极端高温为39.1 ℃。全年无霜期可达303天，年均降雨量为1 304.2 mm。年蒸发量小，相对湿度大，年均相对湿度达83%。植被在全省植被分区中，属南岭西部植被区系。总之，境内群山起伏，土层深厚肥沃，气候温和，无霜期长，雨量适中，植被繁茂，为发展林业生产提供了得天独厚的优越环境[8]。

2 研究方法

2.1数据获取

2010年—2012年，在会同县83块固定标准地附近选择了83株与固定标准地立地条件相近，与马尾松人工林林分平均直径Dg和平均高HD相接近(一般要求相差在5%以下)且干形中等的林木作为平均标准木(解析木)[9]。

将解析木的胸径和冠幅全部进行实测，通过破坏性抽样的方法将样木伐倒，进而测量树高和冠干长度。分别在树干的7/1，3.5/10和1/10树高处(分别代表上、中、下三处)区分干材和干皮称重，然后分别抽取样品；对树枝、树叶取样时要分别上、中、下三层来称重取样，最后选取混合样品。将所抽取的样品带到实验室，放在85 ℃恒温下烘干直到恒重，根据各个样品的鲜质量和干质量来推导计算出样木各器官干质量，然后汇总得到地上部分干质量。在解析木中，约1/3的样木(28株)要用全挖法得到整个根系，然后区分根茎、粗根(≥10 mm)、细根(2～10 mm，不含2 mm以下须根)来称量鲜质量，同样要分别抽取样品并测量其干质量，最后推导计算出树根的干质量。

地上部分干质量与地下部分干质量之和即为解析木全林木生物量，将解析木生物量乘以相应生长级的株数并累加作为林分生物量的估算值[4，10-11]。

2.2数据分析

本研究提出的马尾松全林整体生物量模型是在李桂珍、郭文清等[3]建立的全林整体生长模型的基础上，结合张翼、郭文清等[4]研建的林分蓄积量与各组分生物量相关关系模型，采用两阶段度量误差模型方法[1，5-7]融合模型进行参数的拟合构建而成的，即马尾松全林整体生物量模型是由以下模型融合组成：

两阶段度量误差模型法的原理是采用非线性度量误差联立方程组模型对两个或几个模型进行融合以及参数的重新估计，经过两阶段度量误差模型法融合后的模型有效地解决了模型中不相容的问题。

多元非线性度量误差模型即非线性误差变量联立方程组的向量表达式形式为：

(2)

式中，q维无误差变量的观测值和p维误差变量的观测值分别是xi和Yi，Yi的未知真实值是Yi，m维向量函数是f，方程中误差的协方差矩阵可以为Φ=σ2ψ，ei的误差结构矩阵是ψ，估计误差是σ2[12-13]。由于立木相对生长模型描述生物体各“维量”之间的统计关系相当准确，因此采用下述模型描述变量的关系(即状态方程)：

(3)

式中，x表示树木直径，y1表示树干生物量，y2表示树冠生物量，y0表示地上部分生物量，y0=y1+y2。

由y0=y1+y2推出a1(x)，a2(x)的形式是

a1(x)=c0c1xb0/ (c1xb1+c2xb2)，

a2(x)=c0c2xb0/ (c1xb1+c2xb2)。

(4)

这样，把方程改写为

(5)

取得n组观测值，xi和yi=(yi1，yi2，yi0)，i=1，…，n。直径是可以选定的精确观测的量，认为它是无误差变量(或说外生变量)。观测值yi的误差来自两个方面：观测误差和随机抽样误差，它是状态变量的观测值(内生变量)。因此可以用非线性度量误差模型来做参数估计。非线性度量误差模型的参数不能有冗余，式(5)中存在多余参数，为此，将式(5)改写成

令r1=c2/c1，r2=b2-b1，y0=y1+y2，得到相容性生物量模型的形式：

(7)

由于y0=y1+y2，所以得到非线性联立方程组模型：

(8)

其中独立参数为c=(r1，r2，c0，b0)。

3 结果与分析

3.1模型构建

由于式(1)中的三个方程的参数只是局部化的结果，将三个方程整合为一个系统方程后估计出的参数是不尽相同的。针对此类问题，有学者经过研究提出了采用两阶段度量误差模型(TSEM)的方法来重新估计参数[14]。两阶段度量误差模型方法是对非线性度量误差模型参数估计的一种行之有效的方法。采用非线性误差变量联系方程组的方法，借助唐守正提出的ForStat软件平台来进行参数估计[15]，首先将式(1)进行优化得到：

式中，a，b，b1，b2，b3，b4，b5是模型的参数，L为地位指数，S为密度指数，t为年龄，fH为形高，Y1为林分蓄积量，Y2为林分各器官生物量，可以得到马尾松全林整体生物量模型未经过两阶段度量误差模型方法进行模型融合的参数，如表1所示。

表1 马尾松全林整体生物量模型融合前参数Tab1 TheparametersofPinusmassonianawholestandbiomassmodelbeforeintegration组分abb1全林木002950965719132干002060935719132枝000171124719132叶000480882019132根000860920419132b2b3b4b50841503383098762654208415033830987626542084150338309876265420841503383098762654208415033830987626542

采用ForStat软件计算非线性联立方程组模型的参数，首先在数据窗口里建立数据文件，如图1所示。

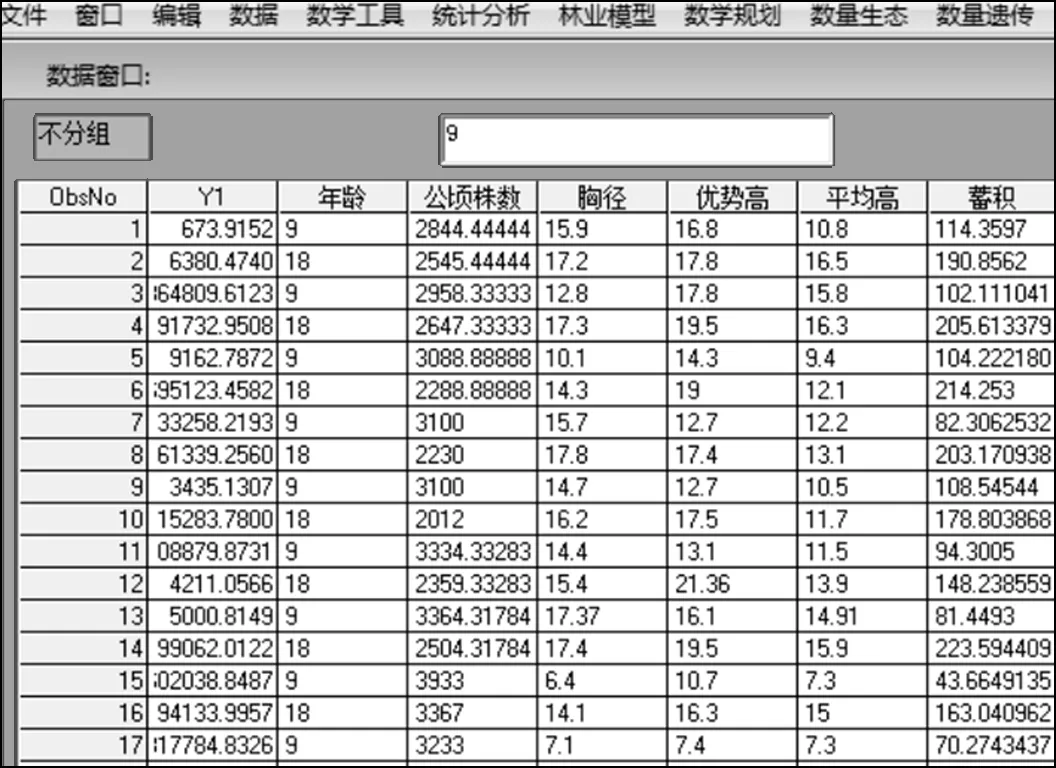
图1 马尾松全林整体生物量模型融合数据窗口(部分)Fig.1 The data window of integrated Pinus massoniana whole stand biomass model

运行程序，单击统计分析，然后单击其中的非线性误差变量联立方程组，结果弹出模型方程组以及模型参数的输入窗口，如图2所示。

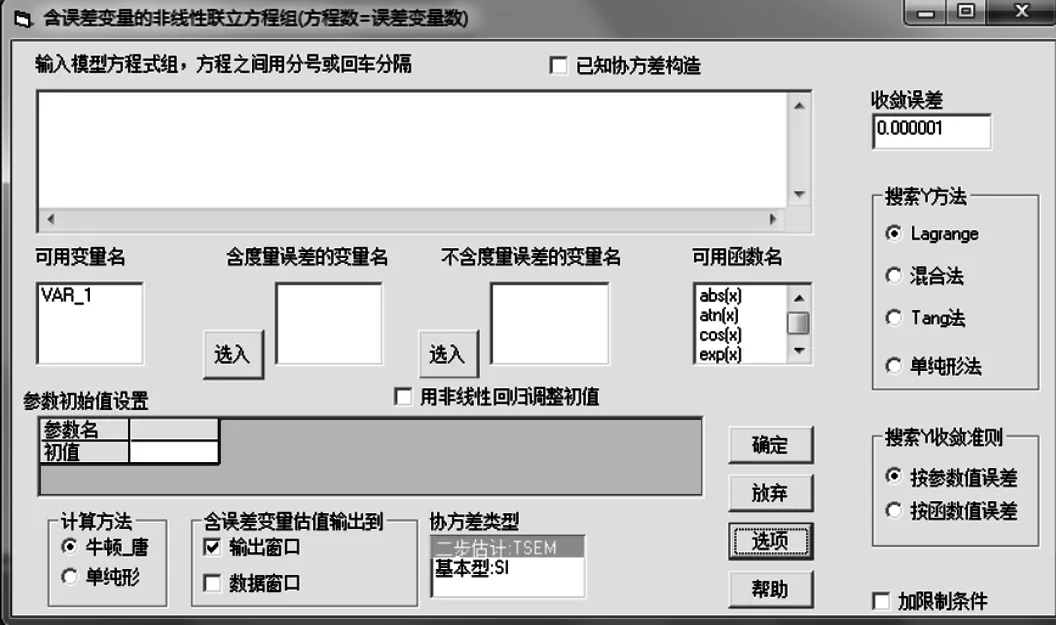
图2 马尾松全林整体生物量模型融合对话框Fig.2 The dialog box of integrated Pinus massoniana whole stand biomass model

在方程组输入框中分别输入有度量误差以及没有度量误差的变量名称，输入模型方程式组，设定参数初始值(a=1，b=1，b1=1，b2=1，b3=1，b4=1，b5=1)，选择模型参数估计方法(牛顿-唐法)、“误差变量”估计方法(Lagrange)、方差结构(TSEM)，指定的允许误差为0.000 001，最后点击确定即可得到马尾松全林整体生物量模型采用两阶段度量误差模型方法融合后参数，如表2所示。

表2 马尾松全林整体生物量模型融合后参数Tab2 TheparametersofPinusmassonianawholestandbiomassmodelafterintegration组分abb1全林木004730953817673干003260972116552枝000130565414374叶000540472113758根000920565714432b2b3b4b50837603062090212439507962028791110221020095430552108953195170630204453074311743207494020970701518916

由表1和表2可以看出，采用两阶段度量误差模型方法对模型进行融合，模型的参数发生了变化。其中，全林木生物量模型的参数以及参数b5的值整体变小，其余参数均发生改变。将以上模型参数分别带入式(2)可得到马尾松全林整体生物量模型。

3.2模型精度检验与适用性分析

通过对非线性误差变量联立方程组模型进行拟合，由模型输出结果可得出方程最大平均绝对误差、最大平均相对误差、Y1、Y2的残差平方和和确定系数，如表3、表4所示。

表3 观测值与估计值平均最大误差Tab3 Theaveragemaximumerroroftheobservedvaluewiththeestimatedvalue组分方程最大平均绝对误差方程最大平均相对误差全林木17763E-1587426E-12干341060E-1348686E-11枝46391E-765321E-8叶21987E-875268E-9根91308E-757914E-8

表4 观测值与估计值精度检验Tab4 Theaccuracytestoftheobservedvaluewiththees⁃timatedvalue组分Y1Y2残差平方和确定系数残差平方和确定系数全林木61000965548094891701003909502干1770378586090233218173309137枝139821974090015743020309094叶84589642089127439201408879根6931784208453112345620827391

方程最大平均绝对误差和最大平均相对误差越小，在一定程度上表示模型的建模精度越高；Y1和Y2的确定系数越大，也在一定程度上表示模型的建模精度越高。由表3、表4 可知，模型的方程最大平均绝对误差和最大平均相对误差均小于误差允许的范围，而且接近无穷小；而各器官生物量的Y1和Y2的确定系数也相对较高，其中，全林木、干和枝的确定系数均达到了90%以上，根的确定系数相对偏小，只有82%左右，但从整体上分析知模型的预测效果较好。

根据马尾松人工林各组分生物量的观测值和估计值输出结果分别作实测值与预测值对比图(见图3)，可以看出Y1的散点比较均匀的分布在直线Y=a+bX的两侧，Y2的散点均匀的分布在直线Y=a+bX的前半部分，可能是由于Y1、Y2的数值大小不一造成的，但并不影响模型的精度。由以上分析可以得出，用度量误差模型方法得到的模型精度较高，并且观测值与估计值的对比结果是无偏的。

图3 马尾松各器官生物量与蓄积量实测值-估计值对比图Fig.3 Comparison chart of the measured value-estimated value of Pinus massoniana organ biomass and volume

由图3分析可知，基于度量误差模型的马尾松全林整体生物量模型的估计期望值和实测值均匀的分布在直线Y=a+bX附近。综合以上分析结果充分说明，采用两阶段度量误差模型法融合后的全林整体生物量模型的精度较高，适用性检验效果较好。

4 结论与讨论

(1)采用两阶段度量误差模型法对马尾松林分蓄积量与各组分生物量回归模型和全林整体生长模型进行融合，并对模型的参数进行重新估计，得到马尾松纯林全林整体生物量模型，融合后的模型参数均发生了改变，其中各组分的b5值整体变小。

(2)通过对全林整体生物量模型的精度检验，表明方程最大平均绝对误差和最大平均相对误差均小于误差允许的范围，而且接近无穷小；而各器官生物量的Y1和Y2的确定系数也相对较高，其中，全林木、干和枝的确定系数均达到了90%以上，根的确定系数相对偏小，只有82%左右，但从整体上分析知模型的预测效果较好；对马尾松纯林各组分生物量的观测值和估计值输出结果分别作实测值与预测值对比图，知观测值与估计值的对比结果是无偏的。综合分析表明，用度量误差模型方法进行融合得到的模型精度较高。

(3)采用两阶段度量误差模型法融合后建立的全林整体生物量模型，精度高，实用性强，解决了如何将森林资源清查的蓄积量转化为生物量这一难题，为大尺度森林生物量建模提供了一种行之有效的新方法，将大大减少森林资源生物量调查统计的工作量。

[1] 温远光. 用蓄积量估测森林生物量的初步尝试[J]. 林业科技通讯，1989(7)：7-10.

[2] 李际平，吕勇. 会同杉木人工林生物产量预估模型研究[J]. 林业科学，1997，33(专刊2)：143-147.

[3] 李桂珍，郭文清，刘沙，等. 马尾松人工纯林全林整体生长模型的研究[J]. 湖南林业科技，2014，41(4)：22-26.

[4] 张翼，郭文清，杨骏，等. 马尾松次生林蓄积量与生物量相关性研究[J]. 湖南林业科技，2014，41(4)：31-34.

[5] 曾伟生，肖前辉，胡觉，等. 中国南方马尾松立木生物量模型研建[J]. 中南林业科技大学学报，2010(5)：50-56.

[6] 曾伟生，夏忠胜，朱松，等. 贵州省人工马尾松立木材积和地上生物量方程研建[J]. 林业科学，2011，47(3)：96-101.

[7] 唐守正，张会儒，胥辉. 相容性生物量模型的建立及其估计方法研究[J]. 林业科学，2000，36(1)：19-27.

[8] 张华英. 基于3S技术的农林复合生态系统景观格局分析——以湖南省会同县为例[D]. 长沙：中南林业科技大学，2003.

[9] 孟宪宇. 测树学[M]. 北京：中国林业出版社，2008.

[10] 马钦彦. 中国油松生物量的研究[J]. 北京林业大学学报，1989，11(4)：1-10.

[11] XUH，WANG M L. Comparison of CAR and VAR biomass models[J].ForestryStudiesinChina，2001，3(1)：32-36.

[12] 唐守正，李希菲. 用全林整体生长模型计算林分纯生长量的方法及精度分析[J]. 林业科学研究，1995，8(5)：471-476.

[13] 唐守正，李勇. 生物数学模型的统计学基础[M]. 北京：科学出版社，2002.

[14] 李永慈，唐守正，李海奎，等. 用两阶段度量误差模型方法和ForStat软件进行模型整合[J]. 林业科学，2004，2(40)：75-78.

[15] 唐守正，郎奎建，李海奎. 统计和生物数学模型计算(ForStat教程)[M]. 北京：科学出版社，2009.

(文字编校：张 珉)

Constructionoftheintegratedstandbiomassmodelofpure
Pinusmassonianaforest

GUO Wenqing1， LI Guizhen2， LIU Sha3， TAN Gangyi4

(1.Hunan Academy of Forestry， Changsha 410004， China；2.Forestry Bureau of Huaihua City， Huaihua 418000， China；3.Forestry Department of Hunan Province， Changsha 410007， China；4.Forestry Bureau of Youxian， Youxian 412300， China)

Taking purePinusmassonianaforest in Huitong County of Hunan Province as research object，using the method of two-stage measurement error model to integrate stand volume and components’ biomass regression model and integrated stand growth model of purePinusmassonianaforest，and reestimate parameters of the model，purePinusmassonianaforest integrated stand biomass model has been obtained.It is known by experience that this model has high accuracy and good adaptability.

integrated stand biomass model；two-stage measurement error model；Pinusmassoniana

2014-10-22

国家林木种质资源平台(2005DKA210003-02-13)。

S 791.248；S 718.55+6

A

1003 — 5710(2014)06 — 0035 — 05

10. 3969/j. issn. 1003 — 5710. 2014. 06. 009