基于小波变换的边缘保留图像去噪改进算法

刘 平，王 磊，郭中华，李树庆

(宁夏大学物理电气信息学院，宁夏银川750001)

数字图像在传输和获取过程中，容易被各种噪声污染而质量下降。因此，寻找一个既能有效去除图像噪声，又可以很好地保留图像敏感信息的方法成为图像去噪的研究热点［1］。

目前，传统的数字图像去噪研究［2－4］多数都是基于空间滤波器的，而这些滤波器通常是通过平滑处理来降低噪声，并未考虑如何有效保持图像边缘等重要特征信息。针对该问题，许多改进方法也相继被提出，例如偏微分方程法、计算机流体动力学法［5］和全变差法［6］等。

近年来，由于小波变换良好的时频分析特性，在图像去噪中得到了广泛的应用［7－8］。基于小波变换的图像去噪方法，其核心是对含噪图像进行小波分解并处理分解后的小波系数，将与噪声相关的系数均置为零或者一个适当的值，然后由处理过的小波系数重构得到去噪后的图像。

阈值法作为小波去噪的主要方法，其关键在于阈值的选取。其中，Donoho等人提出的统一阈值法计算简单，但常因小波系数被“过扼杀”而导致重建时的误差较大［9－10］。针对这一问题，Lakhwinder Kaur等人提出了NormalShrink阈值法［11］，该算法较统一阈值在图像质量和去噪性能两个方面均有很大提升，但仍然存在边缘模糊问题。于是，焦莉莉等人又针对不同的子带特性，提出了一种新的阈值法进行改进，从而提高了图像的视觉效果［12］。但上述方法均为全局阈值法，未考虑噪声在不同小波分解尺度下特性不同的问题。因此，本文提出了一种基于小波阈值法的图像去噪的改进算法，对去噪过程边缘模糊问题进行改善。

1 小波阈值法图像去噪

小波阈值法是常用的图像去噪方法，其过程称为小波萎缩，具体步骤如下:

1)进行离散小波变换;

2)进行阈值估计;

3)使用收缩法则计算阈值;

4)用阈值化后的小波系数进行小波逆变换。

阈值的选取(阈值函数)体现了对于模大于或小于阈值的小波系数的处理策略，常用的有硬阈值和软阈值两种。

硬阈值法中，模小于或等于阈值λ的系数w被置为0，其余的系数则保持不变，即

在软阈值法中，模大于阈值的系数都减去阈值，其他均置为0，即

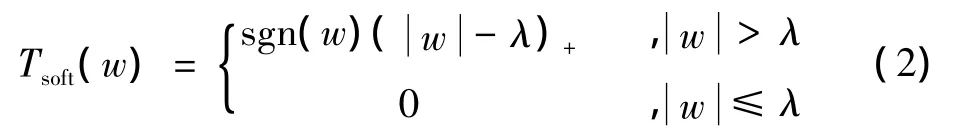
硬阈值法虽然可以在一定程度上保留图像边缘等局部特征，但由于其不连续性，会使图像出现振铃、伪吉布斯形影等视觉失真，而软阈值法处理后的图像相对较为平滑，本文使用软阈值进行处理。

2 保留边缘特征的改进算法

小波除噪的改进算法，其中心思想就是在每个子带中计算一个阈值来提取图像的本地特征。而每个子带阈值分别通过计算噪声级别和边缘强度得到。这种新的阈值方案既可以有效去除图像噪声，又可以很好地保留图像边缘信息。其具体步骤如图1所示。

图1 改进的图像除噪算法原理图

首先，将加入高斯白噪声的图像g分解成m×m个像素块，分别对分解后的像素块逐个进行除噪，除噪过程中利用本地噪声特征和自适应阈值即可得到更好的去噪效果。但是，正如信息被阈值化后会丢失，在分解图像时，相邻像素块的边界同样会受到影响。为了消除这一影响，选择1个n×n(n＞m)的像素区域Bn，Bn包含Bm，最后对Bn区域中每一个像素块分别进行离散小波变换。

边缘检测算法用于识别图像中的边缘成分。基于双正交小波变换的模极大值多尺度边缘检测算法既可以很好地用于识别图像的边缘，又可以有效地分离出每个子块。为了精准地定位图像边缘且区别于噪声成分，首先对图像进行边缘检测，检测出的边缘信息均与其邻域作比较，若其邻域均不属于边缘成分，则停止检测。这种多尺度边缘检测法为每个子带生成一张边缘图像，此图像为二值图像，其中1表示边缘成分，而0表示非边缘成分。

第i层子带的阈值为

因此，各小波系数根据其子带特性被自适应地阈值化。随着分解级数的增加，子带系数变得越来越平滑。

收缩法则根据已生成的各子带的边缘图像来计算阈值，其中与边缘成分相关的系数关联于较小的阈值。对于这些系数，改进算法中提出的阈值λ'通过子带阈值λi和给定的阈值μ来计算得出，即

式中:μ是图像中与边缘相关的系数阈值的权重。

最后，对外部区域Bn中的每一个像素块进行逆小波变换，内部区域Bm中非重叠的像素块则用来重构去噪后的图像f'。

3 实验结果与分析

改进算法法具体在Inter(R)Core(TM)2 Duo CPU，2.19 GHz、1.99 Gbyte 内存的实验环境，MATLAB 2008 平台下进行仿真实验，分别对加入均值为0，方差为10，15，20，30的高斯白噪声的512×512的Tracy和Building图像进行去噪。将改进的保留边缘特征的自适应阈值法去噪结果与维纳滤波(Wiener)、BayesShrink阈值法、VisuShrink阈值法和NormalShrink阈值法的去噪结果进行比较。本文采用的小波基为“bior3.9”，分解尺度为6，加性高斯白噪声均值为0、方差为20。

图2为Tracy和Building图像及其加噪图像。

图2 Tracy和Building图像及其加噪图像

图3为Wiener滤波等方法与改进算法对Tracy图像去噪结果对比。

图4为Wiener滤波等方法与改进算法对Building图像去噪结果对比。

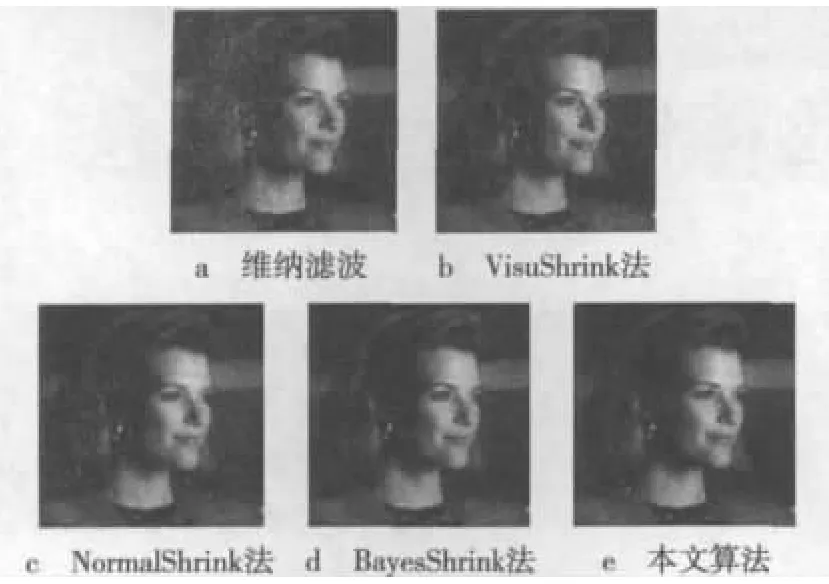
图3 对Tracy图像去噪结果对比

图4 对Building图像去噪结果对比

从图3和图4中可以看出维纳滤波除噪后的Tracy及Building图像丢失了许多边缘特征，且整体除噪能力较弱。由于Visushrink阈值法存在边缘震荡现象且阈值单一，图像重构误差较大。NormalShrink阈值法较Visushrink阈值法虽有所改进，但其去噪结果存在轻微的振铃效应，影响图像整体质量。由于BayesShrink阈值是一种基于Bayes风险最小化的去噪策略，其充分考虑到小波系数的先验统计模型，因此整体去噪效果好于前两种阈值法。从图3、图4中都可看出，Tracy及Building图像整体较为清晰，视觉效果较好。改进算法中子带阈值是通过计算噪声级别和边缘强度得到的，因此去噪后对图像边缘信息保留比较完整。从图3中可以看出Tracy图像人物轮廓以及面部眉骨、鼻梁等突出部位特征保留较为清晰，从图4中也可看出Building图像房屋的轮廓以及窗户、门框和墙角等重要特征保留更为完整。

表 1、表 2 分别给出了 Wiener，VisuShrink，NormalShrink，BayesShrink和改进算法对含有不同级别高斯噪声的Tracy和Building图像去噪后的峰值信噪比PSNR。

从表1、表2中可以看出，改进算法去噪后图像的PSNR较其他方法均有所提高。在表1中，改进算法较NormalShrink法去噪后图像的PSNR平均提高2.6%;表2中平均提高1.5%。从表1和表2中还可看出去噪后的Tracy图像PSNR均大于Building图像，而且随着图像噪声方差的增大，PSNR呈下降趋势，其中去噪后图像PSNR最小的是维纳滤波。

4 结束语

本文在分析了几种现有的小波阈值法的基础上，提出了一种改进的自适应的小波阈值法，该方法可以有效地抑制不同程度的高斯噪声，能很好地保留图像边缘等重要特征信息，仿真结果表明该方法去噪后图像的视觉效果和峰值信噪比都优于BayesShrink等传统小波除噪方法。尽管本文算法在图像去噪时，能够更好地保留图像边缘信息，但是处理速度相对较慢，今后可对提高运行速率进行研究。

［1］ MEHDIN，HOSSEIN N.Image denoising in the wavelet domain using a new adaptive threholding function［J］.Neurocomp Uting，2009，72(4):1012－1025.

［2］ ABREU E，LIGHTSTONE M，MITRA S，et al.A new efficient approach for the removal of impulsive noise from highly corrupted images［J］.IEEE Trans.Image Processing，1996，5(6):1012－1025.

［3］ GARNETT R，HUEGERICH T，CHUIC，etal.A universal noise removal algorithm with an impulse detector［J］.IEEE Trans.Image Processing，2005，14(11):1747－1754.

［4］ LUOWenbin.Efficient removal of impulse noise from digital images［J］.IEEE Trans.Consumer Electronics，2006，52(2):523－527.

［5］ SETHIAN J.Level set methods and fastmarching methods［M］.Cambridge:Cambridge University Press，2009.

［6］ CHAMBOLLE A，VORER，LEEN，etal.Nonlinearwavelet image processing:variational problems，compression and noise removal through wavelet shrinkage［J］.IEEE Trans.Image Processing，1998，7(3):319－335.

［7］刘艳霞，董蓓蓓，刘钰，等.基于小波阈值的医学图像去噪研究［J］.电视技术，2012，36(19):183－185.

［8］郭蕾，田松，许悦雷，等.一种小波自适应萎缩去噪改进算法［J］.电视技术，2012，36(11):27－29.

［9］ DONOHO D，JOHNSTONE I.Ideal spatial adaptation viawavelet shrinkage［J］.Biometrika，1994，81(3):425－455.

［10］ DONOHO D，JOHNSTONE I.Adapting to unknown smoothness via wavelet shrinkage［J］.Journal of the American Statistical Associatio，1995，90(432):1200－1224.

［11］刘薇，徐凌，杨光.基于双树复小波二元统计模型的图像去噪方法［J］.中国图象图形学报，2009，14(7):1291－1297.

［12］焦莉莉，刘丽，马苗.改进的自适应阈值小波图像抑噪算法［J］.中国体视学与图像分析，2009，14(2):152－155.