图像压缩感知中常用测量矩阵的性能比较

詹可军，宋建新

(南京邮电大学图像处理与图像通信实验室，江苏南京210003)

随着信息科技的不断进步，人们对信息的需求日益增加，需要处理和保存的数据量越来越多，在信息的采样和压缩过程中对采样速度和处理速度的要求也越来越高。当前常用的视频编码标准，如MPEG－X，H.264等，通过使用预测编码和可变长编码减少了帧间的冗余度，很大程度上提高了压缩效率。但以上基于奈奎斯特采样定律的视频压缩标准也有其局限性:1)先采样、后压缩，在采样的过程中由于要遵循奈奎斯特采样定律，必然导致产生过多的采样数据要存储，尤其是对视频信号的采样，而庞大的数据量必然会对存储设备提出更高的要求。2)这类视频编码方法产生的视频编码数据对差错非常敏感，有时一个比特的差错都有可能造成解码质量的严重下降甚至无法解码，当传输的延迟、丢包和抖动超过一定值时，视频质量将会迅速下降。基于这些缺点，近几年由D Donoho、T Tao等人提出压缩感知(Compressive Sensing，CS)［1－3］理论，该理论突破了奈奎斯特采样定律的限制，其主要思想是构造适当的测量矩阵对稀疏信号以远低于奈奎斯特采样频率进行多次随机测量，如果测量过程满足约束等距性(RIP)［4］条件，就能通过适当的重构算法从测量数据中恢复出原始信号。由于测量值的数目远小于原始信号的数目，另外压缩感知理论将采样和压缩在一个过程中同时完成，因此待编码的数据量就大大减少，也就降低了对存储设备的要求。其次，由CS理论可知，测量数据中的每个值都包含原始信号的所有信息，因此每个测量值对信号的重构来说是等重要性的，因此重构信号的质量只和重构过程中用到的测量值个数有关，而与具体的哪几个测量值无关，这样在接收端收到的测量值越多，重构出的信号质量就越高，视频编码数据关于信道质量具有很好的可伸缩性。

CS理论突破了奈奎斯特采样定律，如果将其应用到实践中，那么信号的采样和压缩都可以以很低的速率进行，这将显著提高编码效率，降低数据存储和传输的代价，以及信号的处理时间传输成本。压缩感知理论一经提出，就在医学成像、无线通信、图像处理、信号稀疏表示、多媒体编码等领域受到高度关注。

1 压缩感知基本理论

信号在某些变换基下具有稀疏性是压缩感知的前提条件，如果一个信号X∈RN能够在某些稀疏基ΨN×N=［ψ1，ψ2，…，ψN］下稀疏表示为

写成矩阵的形式为

如果稀疏系数α∈R N中只有S≪N个非零值，那么就说该信号在基Ψ下是S稀疏的。压缩感知的采样过程是用一个和稀疏基Ψ不相干的测量矩阵Φ(M×N)(这里Φ的每一行相当于一个传感器，它与原始信号相乘，获得原始信号的一个测量值)和信号X∈R N相乘，即

则可以得到原始信号在测量矩阵上的M个投影，其中每一个线性投影都包含了原始信号的全部信息，因此这M个投影值是同等重要的。

将式(2)代入式(3)可得

式中:ACS=ΦΨ。由于M＜N，所以压缩感知采样是一个降维过程，由测量值y恢复原始信号X是一个解线性方程组问题，但是不可能直接得到方程的解，因为该方程的未知数个数比方程的个数要多，有无穷多解。虽然从y中恢复α是一个病态问题，但是由于稀疏系数α是稀疏的，其中存在很多零值，因此未知数个数也就相应地大大减少，使得由y重构成α成为可能。理论证明，只要矩阵ACS中任意2S列是线性独立的，就存在一个S稀疏的向量α使得y=ACSα成立。

当信号满足在基Ψ下具有稀疏性，且测量矩阵Φ和Ψ满足不相干性，那么压缩感知理论就可以通过求解以下l0范数问题来重建原始信号

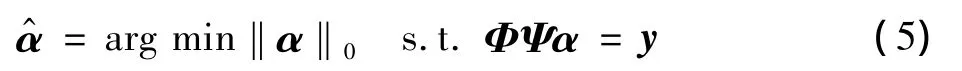
但是求解以上l0范数问题是一个NP－hard的非凸优化问题，理论证明［5－6］，在一定条件下求解l1范数等价于求解l0范数问题，因此可将上面求解过程转化为下面的l1范数求解过程

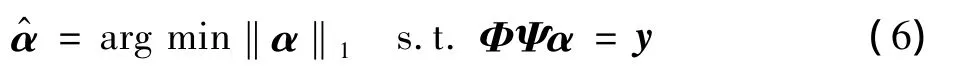
这样就将式(5)转化为一个凸优化问题，进一步可以转化为线性规划问题来求解。目前常用的重构算法有:基于贪婪算法的匹配追踪(MP)［7］、正交匹配追踪(OMP)［8］、正则化的正交匹配追踪(ROMP)［9］、压缩采样匹配追踪(CoSaMP)［10］等算法;基于凸优化算法的梯度投影算法(GPSR)［11］、基追踪(BP)、迭代硬阈值(IHT)等算法;基于Bayesian类统计优化等算法［12］。

2 测量矩阵及其性能

2.1 测量矩阵的性能

测量矩阵的构造是压缩感知的关键部分，由于压缩感知理论中信号的测量过程就是用测量矩阵和稀疏信号相乘，因此测量矩阵的好坏直接影响到重构出来信号质量的好坏。研究测量矩阵所需满足的性质和构造性能优越的测量矩阵一直是压缩感知理论研究的重点。测量矩阵所需满足的性质主要有两点:不相干性和约束等距性(RIP)。构造性能优越的测量矩阵主要是指在达到相同的重构信号质量的前提下，要使所选的测量矩阵只需测量更少的数据即可实现重构要求。通常在选择测量矩阵时要尽量满足以下3个条件:1)用该测量矩阵测量时只需要较少的数据;2)便于硬件实施;3)普遍适用。

影响测量矩阵性能的因素主要有两个:不相干性和约束等距性。测量矩阵和稀疏基之间的相干性定义为

相干性用来衡量随机测量矩阵和稀疏基之间任何两元素间的最大相关性，如果测量矩阵和稀疏基之间包含了相关元素，相干性M就大，反之就小，相干性μ的取值范围为μ(Φ，Ψ)∈［1，］。

在利用式(4)求解稀疏系数的过程中，测量矩阵不仅要满足不相干性还要满足约束等距性，用公式来表述RIP性质为

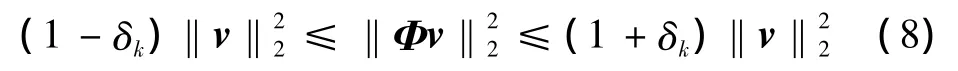
式中:v表示任意具有严格K稀疏的矢量;δk为等距常数，取值范围为δk∈(0，1)。约束等距特性给出了原始信号X和测量信号y的能量约束条件，保证了信号从一个域变换到另一个域收敛不发散。RIP的等价描述为:测量矩阵和稀疏基之间不相干，即Φ的行不能由Ψ的列线性表示，且Ψ的列不能由Φ的行线性表示。

2.2 常用测量矩阵

目前常用的测量矩阵有很多，在不同的文献中经常会碰到不同的测量矩阵，但总体来说目前常用的测量矩阵可以分为两类:随机性测量矩阵和确定性测量矩阵。

Candes和Romberg等学者构造出了常用的随机性测量矩阵，这类矩阵主要有高斯随机测量矩阵、伯努利测量矩阵、部分傅里叶测量矩阵、部分哈达玛矩阵、非相关测量矩阵等，这类矩阵已被证明满足RIP性质，这类矩阵由于和绝大部分信号不相关，因此在相同的重构质量要求下只需较少的测量值即可实现，而且构造简单，因此在实际中应用很广泛，但是这类矩阵也有其固有缺点，就是其元素具有不确定性，所需的存储空间较大，不利于硬件实现。

由于随机性测量矩阵存在诸多缺点，因此有学者就提出了确定性测量矩阵的概念，目前常用的确定性测量矩阵有利用元素循环移位来构造的托普利兹测量矩阵和循环测量矩阵，利用多项式方法来构造的多项式测量矩阵，还有二进制稀疏测量矩阵、结构化随机测量矩阵等。顾名思义，这类矩阵只需一小部分元素即可确定剩余的大部分元素，因此所需的存储空间少，确定性测量矩阵的另一个优势就是由于其元素的确定性，因此在硬件实现方面容易实现，因此得到很高的关注。由于本文的最终目的是将压缩感知理论应用于实际生活中，因此以后的研究重点也会偏向于确定性测量矩阵。

下面将对目前常用的几种测量矩阵进行性能比较，主要比较使用率较高的高斯随机矩阵、部分哈达玛矩阵、托普利兹矩阵、伯努利矩阵和稀疏随机矩阵。

2.3 本文实验方案

本文实验方案的主要思想是将读入的图像分为n×n不重叠的小块，然后对每个块用相同的压缩感知测量与重构方法进行编解码。处理流程如图1所示。

图1 本文图像处理流程图

在图1中，主要对块大小分配模块、测量率分配模块、压缩感知测量模块分别进行变量测试。分别统计在不同图像分块大小n×n、不同测量率(M/N)和不同测量矩阵的条件下重构信号的峰值信噪比、重构时间和视觉质量。通过对实验数据的分析对比，得出分块大小、测量率、测量矩阵对压缩感知信号重构的影响。

3 实验结果与分析

本节主要对目前常用的几种测量矩阵进行详细的性能分析和比较，参与分析比较的几种矩阵为高斯随机矩阵、部分哈达玛矩阵、托普利兹矩阵、伯努利矩阵、稀疏随机矩阵。主要从以下几个方面对这几种矩阵进行分析比较:不同测量率下的峰值信噪比(PSNR)、不同测量率下的重构时间(time)、主观视觉质量。由于本文所采用的编码方法是基于分块的处理方法，所以将不同分块大小(n×n)对重构信号的影响也考虑在内。仿真图像为255×255的Lena图像，仿真环境为Windows7操作系统，CPU主频为2.2 GHz，运行软件MATLAB2010b。由于这几种矩阵每次产生都有一定的随机性，因此本实验的所有实验结果都是运行100次后的平均值，另外，本文的实验数据都是采用正交匹配追踪(OMP)算法得出的结果。首先用8×8的分块大小来研究不同测量矩阵的性能。

实验中所用的测量率从低到高依次为25%，37.5%，50%，62.5%，75%，从图2可以看出在25%测量率时，各测量矩阵重构信号的PSNR相差不大，基本都在25～26 dB，但当测量率提高时，各测量矩阵重构图像的PSNR有较大的差异，比如在测量率为37.5%时，稀疏随机矩阵的结果和随机高斯矩阵的结果相差2 dB左右，在测量率为75%时，部分哈达玛矩阵和稀疏随机矩阵的结果也相差2 dB左右。从总体上来看，部分哈达玛矩阵的重构效果比较均衡稳定，要好于其他几种矩阵。下面再从重构时间上来比较几种测量矩阵的性能。

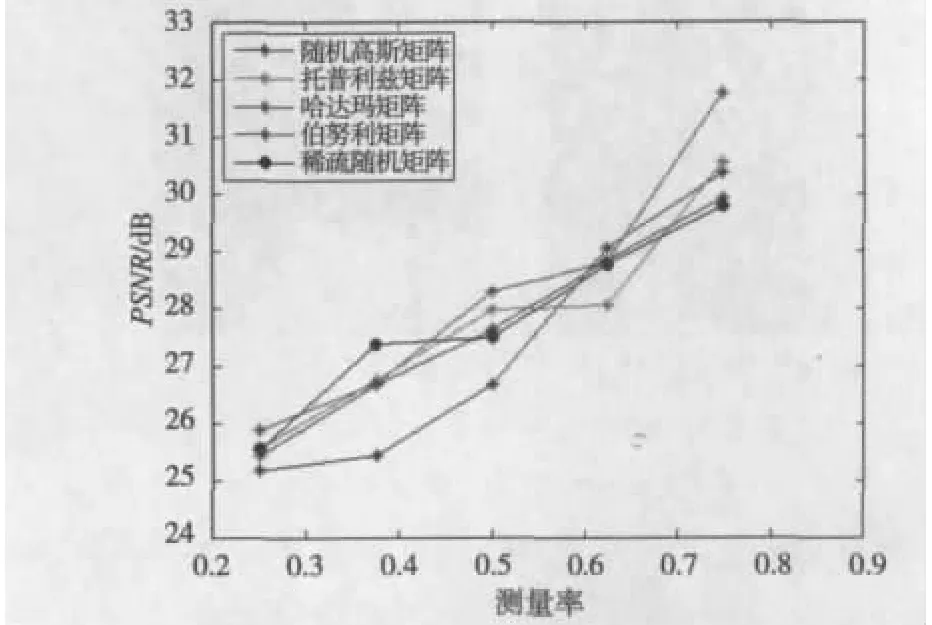
图2 分块大小为8×8时不同测量率下几种测量矩阵重构信号的PSNR

从表1可知，在8×8的分块大小下，几种测量矩阵的重构时间基本在同一数量级，总体上都在0.8～1.0 s之间，区别不大。下面的实验结果是在测量率为50%时，各个测量矩阵重构出来的图像的视觉效果。

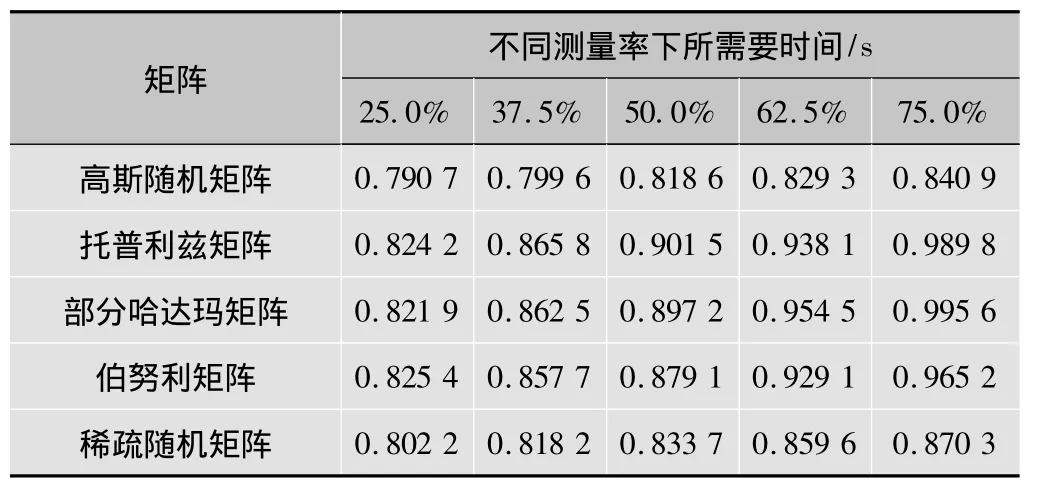
表1 不同测量率下几种测量矩阵重构信号所需时间

从图3可以看出，在测量率为50%，分块大小为8×8时，几种测量矩阵重构出来的图像视觉效果都不是很清晰，模糊效果较为严重，相比之下，哈达玛矩阵和托普利兹矩阵的重构效果相对清晰于其他几种矩阵。

由于实验方案是将图像基于块进行处理的，下面分析一下分块大小对实验结果的影响，从上面的几组数据可以看出，哈达玛矩阵的性能相对来说要好于其他几种矩阵，因此就以哈达玛矩阵为测量矩阵来分析分块对实验结果的影响，其中测量率定为50%。表2是分块大小分别为8×8，16×16，32×32，64×64时哈达玛矩阵重构出图像的PSNR和重构时间。

图3 测量率为50%，分块大小为8×8时各测量矩阵重构图像的视觉效果

表2 测量率为50%时不同分块大小下部分哈达玛矩阵重构信号的PSNR和重构时间

从重构图像的PSNR来看，分块大小为8×8时效果最好，比其他分块大小要高出1～2 dB，而分块大小为16×16，32×32，64×64时重构效果基本相同，区别不大。从重构时间方面来看，分块大小为8×8时的重构时间略长于分块大小为16×16时的重构时间，总体趋势是随着分块大小的增大，所需的重构时间越长，当分块大小为64×64时重构时间已经是分块大小较小时重构时间的4倍左右。从以上分析可以看出，分块大小为8×8时具有最佳的重构效果。

4 总结

本文对目前几种常用的测量矩阵的性能做了一个全面的分析与比较，从重构图像的PSNR、重构时间、视觉效果等方面做了综合对比，总体来说，哈达玛矩阵和托普利兹矩阵相对好于其他几种矩阵，其他几种矩阵的性能基本上没有多大差异。另外本文还对不同分块大小对压缩感知重构信号的影响做了分析，从实验结果来看，综合考虑重构图像的PSNR和重构时间，分块大小为8×8时可获得最佳的重构效果。

［1］ DONOHOD.Compressed sensing［J］.IEEE Trans.Information Theory，2006，51(4):1289－1306.

［2］ CANDESE.Compressive sampling［J］.Proceedings of the International Congress of Mathematicians，2006(3):1433－1452.

［3］ DONOHO D，TSAIC Y.Extensions of compressed sensing［J］.Signal Processing，2006，86(3):533－548.

［4］ DONOHO D.Formost large underdetermined systems of linear equations the minimal l1－norm solution is also the sparsest solution［J］.Comm.Pure Appl.Math，2006，59(6):797－829.

［5］ CHEN S，DONOHO D，SAUNDERSM.Atomic decomposition by basis pursuit［J］.Society for Industrial and Applied Mathematics，2001，43(1):129－159.

［6］ DONOHO D，ELAD M，TEMLYAKOV V.Stable recovery of sparse overcomplete representations in the presence of noise［J］.IEEE Trans.Information Theory，2006，52(1):6－18.

［7］ MALLAT S，ZHANG Z.Matching pursuits with time－frequency dictionaries［J］.IEEE Trans.Signal Processing，1993，41(12):3397－3415.

［8］ JOEL T，GILBERT A.Signal recovery from random measurements via orthogonal matching pursuit［J］.IEEE Trans.Information Theory，2008，53(12):4655－4666.

［9］ DEANNA N，ROMAN V.Uniform uncertainty principle and signal recovery via regularized orthogonal matching pursuit［J］.Foundations of Computational Mathematics，2009，9(3):317－334.

［10］ DEANNA N，JOEL T.CoSaMP:Iterative signal recovery from incomplete and inaccurate samples［J］.Applied and Computational Harmonic Analysis，2009，26(3):301－321.

［11］ FIQUEIREDO M，NOWAK R，WRIGHT S.Gradient projection for sparse reconstruction:application to compressed sensing and other inverse problems［J］.IEEE Journal of Selected Topics in Signal Processing，2007，1(4):586－598.

［12］ JIS，XUEY，CARIN L.Bayesian compressive sensing［J］.IEEE Trans.Signal Processing，2008，56(6):2346－2356.