用反投影滤波算法实现CT图像的ROI重建

洪贤勇，乔志伟

(中北大学计算机与控制工程学院，山西太原030051)

计算机断层成像技术(Computed Tomography，CT)是现今较好的无损检测技术之一，已广泛应用于人体组织成像和工业无损检测中［1－2］。CT算法主要包括解析法和迭代法［3］两种，由于解析法具有重建时间快的特点而处于主导地位，解析法中具有代表性的是滤波反投影(FBP)算法和反投影滤波(BPF)算法。

FBP算法出现于20世纪60年代，并很快从平行束扫描模式推广到圆轨道锥束扫描模式。然而，1984年提出的FDK算法只是一种近似算法，此后近二十年，研究者们一直在寻找精确解析三维FBP算法。2002年到2004年，Katsevich提出了螺旋锥束FBP算法以及一些改进算法［4－5］，这一算法具有公式简单、易于实现等优点，是精确三维锥束CT的一个重大突破，但是这是一种全局重建算法，在处理小物体时具有优势，当处理比较大的物体时，并且只需要重建物体局部的图像时，这种算法就出现了局限性。2004年，潘晓川课题组提出了一种基于PI线的BPF算法［6－7］，由于这一算法是通过求导、反投影、滤波(有限希尔伯特变换)来重建图像，因而在处理数据截断时具有很好的效果［8－9］，而且该算法能够实现局部重建［10－11］。

为了实现精确的局部重建，本文在三维螺旋锥束BPF算法的基础上，设计了一种利用微分和有限希尔伯特变换的局部特性来重建局部图像的平行束BPF算法，这一算法能够实现精确的局部重建，而且有效解决了重建过程中出现的亮条伪像问题［12］，在工程中具有很好的实用性。

1 BPF重建算法的原理

BPF算法是由芝加哥大学潘晓川研究组提出的，其最初形式是针对螺旋锥束三维CT扫描几何的。

后来，该组将这种方法推广到了任意扫描几何轨迹;又将该算法改写成了扇形束二维CT的形式。

本节将分析该算法的原理、关键技术、实现公式及有限希尔伯特变换的实现步骤。

1.1 算法实现的框架图

根据螺旋锥束三维CT的基于PI线的BPF算法，将重建的基本步骤和思想移植到平行束二维CT，可以得到图1所示的重建步骤。

图1 BPF算法的流程图

但是该步骤只是一种重建思想的移植，所以1.2节，给出了算法的推导。

1.2 平行束BPF算法

1)斜变滤波可以分解为微分和希尔伯特变换［13］。

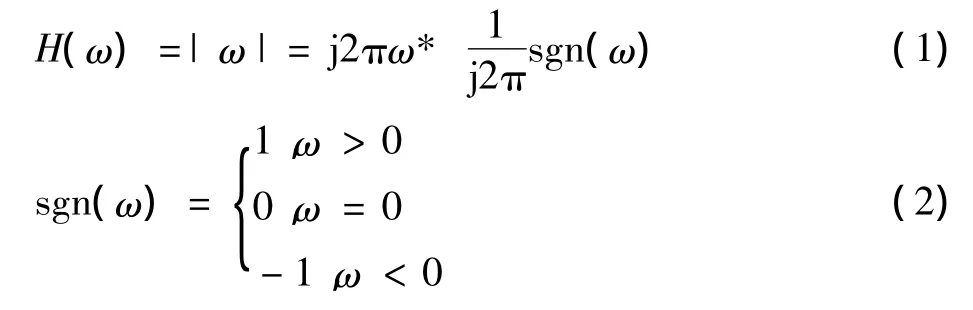
傅里叶变换的两个性质:

(1)在傅里叶域中乘以j2πω相当于在空域(s域)中求导。

由以上两个性质可知，经典的FBP算法可以分解成由微分、希尔伯特变换和反投影三部分组成，改变它们之间的顺序可以实现不同的算法，本文算法来源于上面的基本思想，但是具体的实现公式是基于潘晓川的BPF重建公式并假定平行束扫描几何是螺旋锥束扫描几何的特殊形式而改写得到的。

2)本文算法的实现公式［14］

(1)对每个角度下得到的平行投影数据取ROI区域投影并求导，得到局部微分投影。

式中:p(t，θ)是在角度θ下的投影;p'(t，θ)是投影信号的微分。

(2)对这一局部微分投影反投影到ROI区域，反投影对应的角度范围为0～π。

式中:t=xcosθ+ysinθ;(x，yπ)是平面上的一点，x是该点在x轴上的坐标，yπ是该点在y轴上的坐标，也是PI坐标轴的坐标。注意，在这里PI线是平行于y轴的。

(3)对反投影图像沿着PI线(如图2)进行有限Hilbert变换，得到物体的ROI重建图。

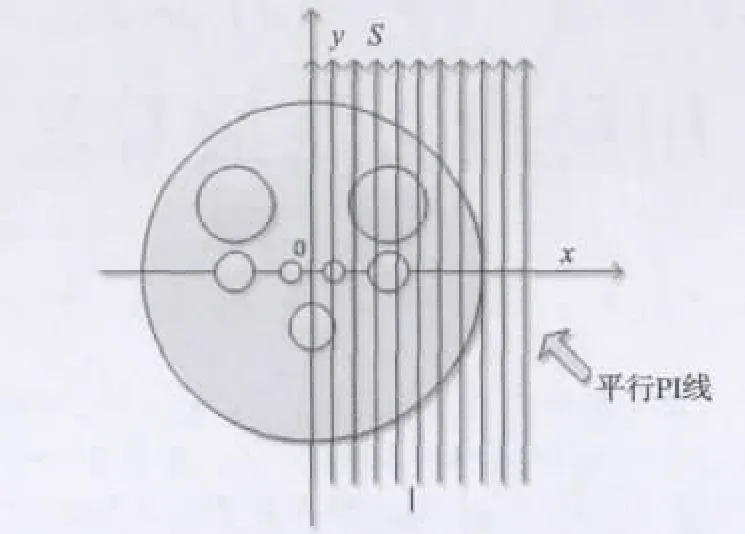
图2 局部平行PI示意图

式中:l，s分别为PI线的两个端点，如图2所示;C(0)为沿着PI线方向的投影，也就是当旋转角度为0时的投影，物体的平行旋转投影图见图3。

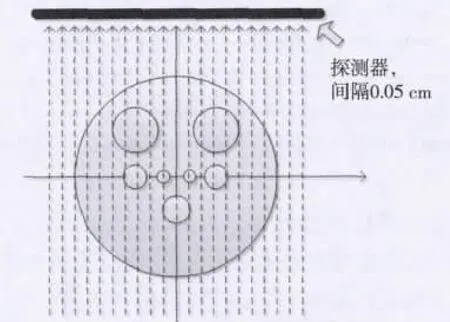
图3 实验用仿真模型投影图

1.3 有限希尔伯特变换的实现步骤

在整个算法中，有限希尔伯特变换的实现方式是最关键的一个步骤。如果处理不好，将使得图像的两边有亮条状伪像。

本文在实现该变换的时候，采用了加权希尔伯特变换的方式，完全避免了这种伪像。

具体的实现步骤如下:

1)第一步，对PI线上的反投影图像做加权，得到

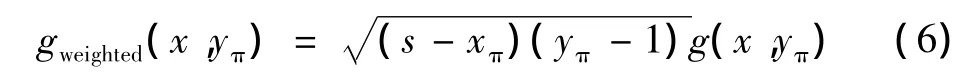
2)第二步，对每个PI线上的反投影加权图像，做一个无限希尔伯特变换，并取值［l，s］;

2 仿真实验及其结果分析

2.1 实验仿真模型说明

在1个由7个小圆柱内插到1个大圆柱的某断层中利用反投影滤波算法进行重建，实验所用仿真模型见图3。探测器在每个角度分别采集201个点(采样间隔为0.05 cm)，共采集180个角度的投影数据(角度间隔为1°)，采用像素驱动方式进行反投影，卷积运算的方式实现滤波，重建出的图像为以旋转中心为中心、大小为201×201的整体重建图。实验模型的参数见表1。

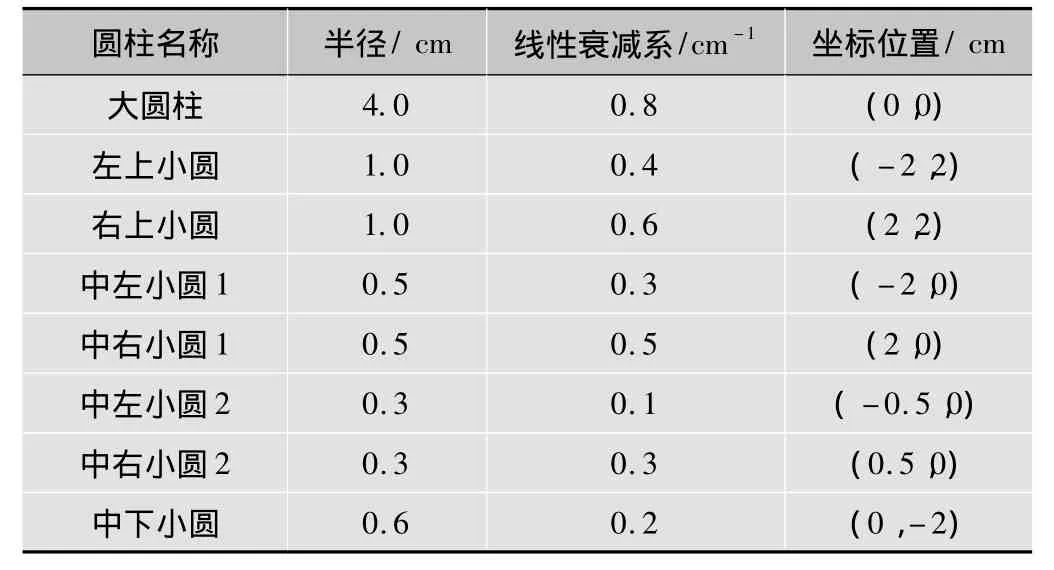
表1 实验模型的参数说明

2.2 实验结果

首先用FBP算法和BPF算法做完全重建(整体投影正弦图见图4);然后以右边半圆作为ROI区域，取仅仅覆盖ROI区域的局部投影(见图5)，用FBP和BPF两种算法重建。

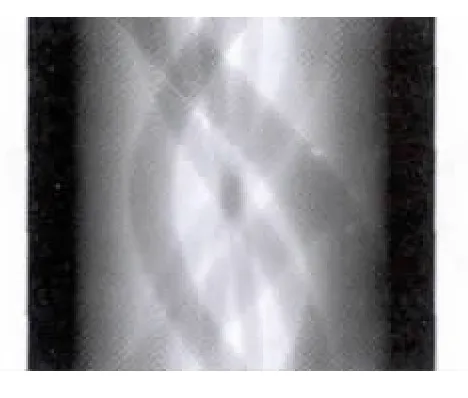
图4 投影正弦图

图5 右半圆投影正弦图

2.3 结果分析

由于FBP算法和BPF算法重建的整体图都是精确重建，因而引入归一化均方距离判距d和归一化平均绝对距离判距r来分析FBP算法和BPF算法的精度［15］(比较结果见表2)

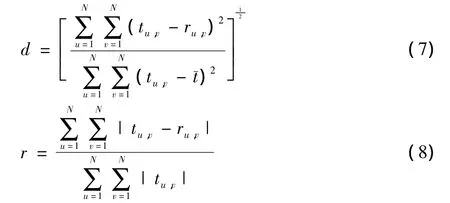
式中:tu，v，ru，v分别表示原始模型和重建后的图像的第u行、v列的像素密度;为测试模型密度的值;图像的像素为N×N。由式子分析可知d越大标明与原始图像的区别越大，也就是说图像越不准确，而r也类似的说明与原始图像的误差，不过它侧重反映出现多数点存在小误差的情况。

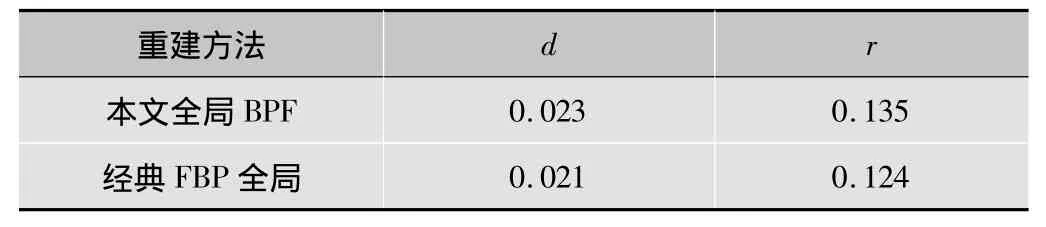
表2 本文全局算法与经典FBP全局算法误差比较

分析图6和图7，以及表2中的数据，可以看出本文所对应的全局重建算法可以达到精确重建的目的，而且其精度与FBP的精度相当。

图6 BPF算法整体图

图7 FBP算法整体图

分析图8和图9，两者所取的局部微分投影一致，但是所使用的算法不同，前者使用本文提出的BPF局部重建算法，后者则是经典的FBP重建算法。图9重建的图像出现了数据的丢失，而图8则显示了精确的局部重建图像，这是由于本文算法具有局部重建的特性，而FBP算法不具备这一特性，由此可以看出本文算法能够实现精确的局部重建。

图8 BPF右半圆图

图9 FBP右半圆图

另外要特别指出的是，图8没有出现先前文献中所出现的顶部和底部的亮条伪像，其根本原因是采用了1.3节所描述的有限希尔伯特变换实现算法。

3 小结

本文的算法是根据潘晓川BPF算法的基础上设计的，通过对ROI区域投影数据求导，然后反投影到ROI区域，最后沿着PI线进行有限希尔伯特滤波得到局部重建图像，仿真实验的结果说明，本文算法所对应的全局重建是一种精度很高的重建算法;当所取的局部投影区域和重建区域一致时，可以精确重建出局部图像，也就是在投影覆盖ROI而且仅仅覆盖ROI时能够实现对这一局部区域的精确重建，说明本文的算法是一种精确的局部重建算法。

当遇到大物体的时候，一般只需要分析物体某一部分或者检查某一部分是否出现问题，此时采用这种方法，一方面可以减少射线剂量，另一方面可以快速重建。可见BPF算法是一种快速有效的ROI重建方法。

［1］张朝宗，郭志平，张彭，等.工业CT技术与原理［M］.北京:科学出版社，2009.

［2］谢强.计算机断层成像技术［M］.北京:科学出版社，2006.

［3］ JIANGM，WANG G.Convergence studies on iterative algorithms for image reconstruction［J］.IEEE Trans.Medical Imaging，2003，22(5):569－579.

［4］ KATSEVICH A.A general scheme for constructing inversion algorithm for cone beam CT［J］.International Journal of Mathematics and Mathematical Science，2003(21):1305－1321.

［5］ YU H，WANG G.Studies on artifacts of the Katsevich algorithm of spiral cone－beam CT［J］.Proceeding of SPIE，2004(35):540－549.

［6］ ZOUY，PANX.Exact image reconstruction on PI－lines fromminimum data in helical cone beam CT［J］.Phys.Med.Bio.，2004，49(6):941－959.

［7］ ZOUY，PAN X.Image reconstruction on PI－linesby useof filtered backprojection in helical cone－beam CT［J］.Phys.Med.Bio.，2004，49(12):2717－2731.

［8］ ZOU Y，PAN X，SIDKY E.Image reconstruction in region－of－interest from truncated projections in a reduced fan－beam scan［J］.Phys.Med.Bio.，2005，50(1):13－27.

［9］ YE Y，YU H，WEI Y，et al.A general local reconstruction approach based on truncated［EB/OL］.［2013－06－10］.http://www.hindawi.com/journals/ijbi/2007/063634/abs/.

［10］ PAN X，ZOU Y，XIA D.Image reconstruction in peripheral and central region－of－interestand data redundancy［J］.Med.Phys.，2005，32(3):673－684.

［11］ ZOU Y，PAN X，SIDKY E.Theory and algorithm for image reconstruction on chords and within regions of interest［EB/OL］.［2013－06－10］.http://www.ncbi.nlm.nih.gov/pubmed/16304723.

［12］谷建伟，张丽，陈志强，等.基于平行PI线的平行束CT重建［J］.清华大学学报，2007，47(3):393－395.

［13］乔志伟.能消除CT角误差的斜变滤波器长度选择方法［J］.计算机工程与设计，2012，33(4):1486－1490.

［14］李亮，陈志强，张丽，等.潘晓川教授的反投影滤波(BPF)新型重建算法介绍［J］.CT 理论与应用研究，2006，15(3):68－73.

［15］李铮.CT重建算法的理论及综合应用的研究［D］.沈阳:东北大学，2005.