基于R－L－MS－L滤波函数的CT图像重建

王晓鹏，王明泉，侯慧玲

(中北大学仪器科学与动态测试教育部重点实验室，山西太原030051)

CT重建算法分为解析法与迭代法两大类，解析法中的卷积反投影算法(CBP)广泛应用于商业和工业中，滤波函数的选择是其中的关键。滤波器的作用是消除反投影过程中的星形伪影，其频率响应理论上要求H(ρ)=，ρ为空间频率，其频带无限，根据佩利－维纳准则，这种滤波器是无法获得的，可通过其进行加窗处理实现，即H(ρ)=W(ρ)，其中W(ρ)为窗函数。常用的窗函数是矩形窗和sinc函数窗，对应的滤波函数为R－L滤波函数和S－L滤波函数。R－L滤波函数的优点是形式简单实用，重建图像轮廓清晰，缺点是有Gibbs效应，表现为明显的振荡，当有噪声时重建质量较差。S－L滤波函数的优点是重建的图像振荡响应较小，对噪声具有一定的抑制作用，缺点是由于其在低频段偏离了的缘故，所以其在低频段的重建质量没有R－L滤波函数高［1］。因此针对它们的缺点，必须要对重建过程中的滤波函数进行改进。人们在此之后提出了将两种滤波函数进行混合的R－L－S－L滤波函数［2］，对两者各自的优缺点进行了折衷，取得了一定的效果。文献［3］从理想函数的概念出发提出了一种新的滤波函数，记为New滤波函数，其表达为

文献［4］通过将R－L与New滤波函数混合得到一种滤波函数，记为R－L－New滤波函数，表达式为

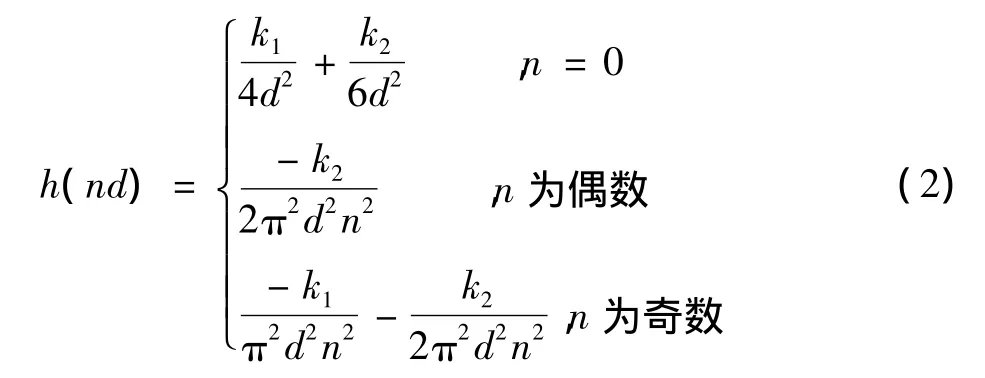
本文在前人的基础上提出了一种新的滤波函数。通过仿真实验分析，新滤波函数比传统的滤波函数对噪声有更好的抑制作用，也能很好地抑制振荡。它将空间分辨率和密度分辨率做了很好的综合，得到了较好的重建效果。

1 新滤波函数的构建思路

滤波函数的选取主要考虑3个因素:主瓣、近邻旁瓣以及远处旁瓣。主瓣越高越窄，空间的分辨率就越好。旁瓣越小，数值精度越高，密度分辨率越高［5］。从信号与系统的角度，可以利用加权平均的思想，使主瓣变低旁瓣变小，以牺牲一定空间分辨率来提高密度分辨率。经典的S－L滤波函数的采样序列为

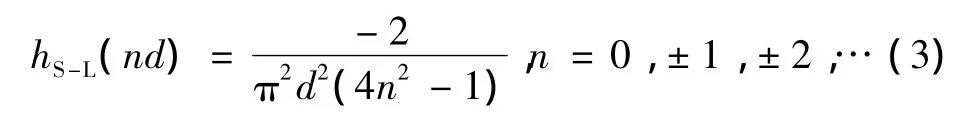
进行加权平均的时候并不是用的点越多越好，当大于3点时，滤波函数的性质将严重变坏，没有必要选取［6］。因此对S－L滤波函数进行3点加权平均，记为MS－L滤波函数，其采样序列为

即

图1和图2分别为 R－L，R－L－New 和 MS－L三种滤波函数主瓣和远旁瓣的离散分布。对比可以发现R－L滤波函数的主瓣高而窄，空间分辨率较好，但是它的远旁瓣幅度和宽度都较大，所以Gibbs效应很严重。而MS－L滤波函数的主瓣较低且宽，但是它的旁瓣收敛快，有利于抑制Gibbs效应和噪声，密度分辨率高。R－L－New介于两者之间。由此可以得出在设计滤波函数的时候可以兼顾空间和密度分辨率，从整体提高重建质量。

图1 各种滤波函数的空域主瓣分布

受混合滤波思想的启发将R－L滤波函数与MS－L滤波函数进行线性混合得到一种新的混合滤波函数，它的冲击响应为

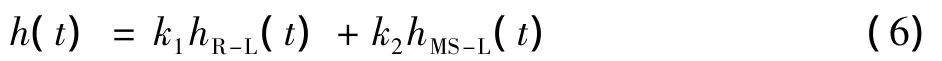
式中:k1≥0，k2≥0，k1+k2=1。k1，k2的值是可以调节的，当k1=0时，它是R－L滤波函数，当k2=0时，它是MS－L的混合滤波函数，其采样序列为

图2 各种滤波函数的空域主瓣分布

2 实验仿真与结果分析

本文对二维Shepp－Logan模型［7］分别使用 R－L滤波函数、R－L－New混合滤波函数和本文滤波函数进行平行束重建。对得到的投影加入均值为0、方差为1的高斯噪声，噪声强度为5%。为了评价重建后的图像质量，本文采用归一化均方距离对图像进行评价，即

式中:tu，v，ru，v分别表示测试模型和重建后图像中各点的像素密度;为测试模型密度的平均值。d较敏感地反映少数点的大误差情况，d值越大表示两者偏差越大［1］。图3a为原始Shepp－Logan，图3b为其横线部分，即第128行的灰度曲线。图4～图6分别为利用R－L，R－L－New和R－L－MS－L滤波函数重建后的结果和对应横线部分的灰度曲线。

图3 原始图

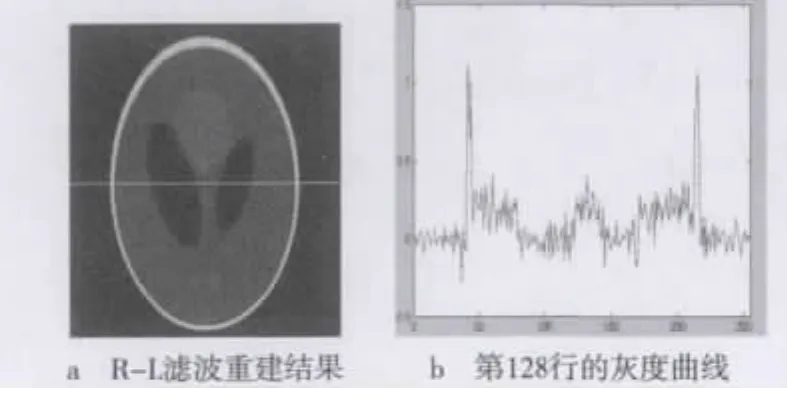
图4 R－L滤波结果

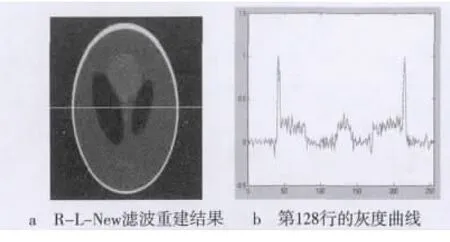
图5 R－L－New滤波结果

通过图4～图6的对比可以看出新滤波函数比R－L和R－L－New滤波函数重建后的图像更加平滑且更接近原始图像。

为了研究不同的噪声强度对重建质量的影响，在投影中分别加入强度为5%，10%，20%的高斯噪声，然后分别利用R－L，R－L－New 和R－L－MS－L 滤波函数进行重建。并利用式(8)作为评价标准得到表1。

表1 3种滤波函数在不同噪声强度下的归一化距离

通过对表1的定量分析可以看出，在不同噪声强度下利用本文滤波函数重建图像的归一化均方距离更小，比R－L－New滤波函数的抗噪声性能更好。

为了研究系数k1对R－L－MS－L滤波函数的影响，选取不同的值重建，得到系数与归一化均方距离的关系，如图7所示。通过观察可以看出，在无噪声的情况下本文滤波函数选取的最佳k1为0.7左右。此时可以更好地抑制振荡与噪声。

图7 不同k1时的归一化均方距离

对实验室采集到的360幅1 024×1 024的火箭发动机模型投影数据进行FDK重建。图8a和图8b分别是采用R－L－New和新滤波函数重建的第150层的切片图像，从图中可以看出采用R－L－MS－L滤波函数重建的图像细节信息更加清晰，图像质量更好。

图8 R－L－New和新滤波重建结果

3 小结

本文通过结合混合滤波器和多点加权平均的思想提出了一种新的滤波函数即R－L－MS－L滤波函数。通过实验与仿真，从定性和定量两个角度都可以看出，R－LMS－L滤波函数比传统的R－L和R－L－New滤波函数重建后的图像质量都要好。它有效抑制了图像重建时的振荡，使重建后的图像更平滑，且其抗噪声性能比传统的滤波函数更高。在无噪声的情况下选择k1=0.7，可以较好地改善重建图像的空间分辨率和密度分辨率。

［1］庄天戈.CT原理与方法［M］.上海:上海交通大学出版社，1992.

［2］翟静，潘晋孝.混合滤波函数在FDK中的应用［J］.南昌航空大学学报:自然科学版，2007，41(S1):263－266.

［3］ WEIY，WANG G，HSIEH J.An intuitive discussion on the ideal ramp filter in computed tomography(1)［J］.Computers＆ Mathematics with Applications，2005，49(5):731－740.

［4］张斌，潘晋孝.CT图像重建的新型混合滤波器［J］.微计算机信息，2009，25(3):298－308.

［5］石本义，王成等，陈四海.CT断层重建中滤波函数设计的新方法［J］.CT 理论与研究，2010，19(4):35－43.

［6］刘晓，杨朝文.RL滤波函数的改进对卷积反投影图像重建的影响［J］.四川大学学报:自然科学版，2004，41(1):112－117.

［7］ SHEPP L，LOGAN B.The fourier reconstruction of a head section［J］.IEEE Trans.Nucl.Sci.，1974，21(3):21－43.