钢支撑束柱抗震性能试验研究
陆 烨,刘 青,李国强,刘玉姝
(同济大学a.土木工程学院;b.土木工程防灾国家重点实验室,上海 200092)
钢结构束柱体系是一种新型结构体系[1],其基本思想是将传统的单柱分成2根柱构成束柱以解决钢框架结构平面布置中梁柱错位搭接的问题(图1)。通过在束柱中间设置传统的抗侧力构件,如钢支撑等,就形成了新型组合束柱构件:钢支撑束柱。钢支撑束柱可以在工厂预制,不但可以承受来自楼面的竖向荷载,更能抵抗风、地震等水平荷载,成为结构的水平抗侧力构件。而且,由于组合束柱构件本身具有较大的承载力和刚度,可以吸收大部分水平荷载,钢框架其他现场梁柱连接节点可设计为铰接或者半刚接,这样,钢结构束柱结构体系具有易于预制装配化的特点(图1)。
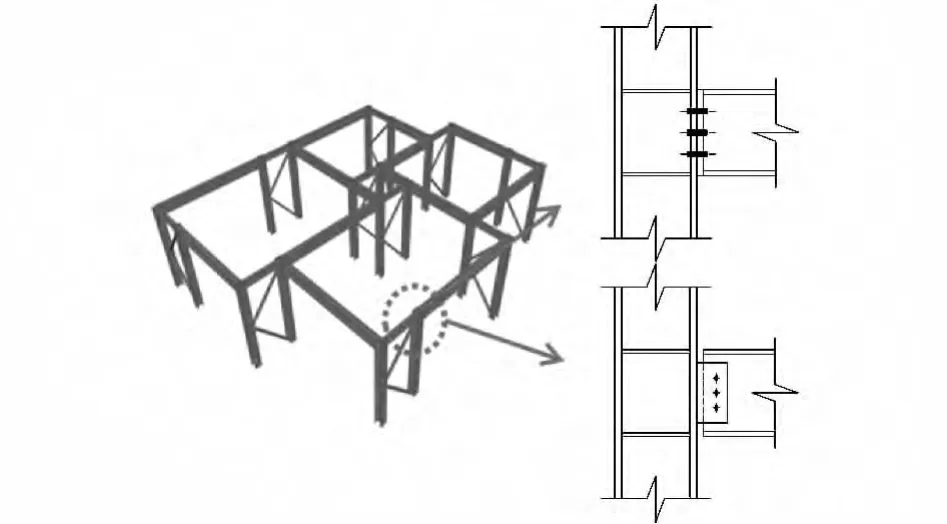
图1 易装配的钢结构束柱体系[1]
钢支撑性能的研究已经很成熟,工程设计中可供选择的支撑形式也相当丰富。首先,支撑的截面形式多种多样,如 H型钢、角钢以及钢管等。Astaneh-Asl等[2-3]系统地研究了角钢组成的支撑杆的抗震性能,包括平面内屈曲的短肢合并双角钢支撑[2]和平面外屈曲的长肢合并的双角钢支撑[3],以及等肢角钢组成的T形及箱形截面支撑[4]。其次,支撑的布置方式根据不同的建筑结构或使用要求,有中心支撑和偏心支撑,其中,中心支撑又分为X型、V型、∧型和单斜杆型等。Goel等[5]试验研究了X型单角钢和双角钢支撑的滞回性能。再次,根据支撑的抗侧性能不同,还可分为普通支撑和屈曲约束支撑(或称防屈曲耗能支撑)[6]。对于框架钢支撑体系的抗震研究也较为深入。Jain等[7]和Ikeda等[8]分别提出了钢框架支撑结构的复杂滞回性能模型,Tremblay等[9-10]分析了钢框架支撑结构的地震响应,Maheri等[11]介绍并研究钢支撑在混凝土结构中的应用及抗震性能,Kim等[12]给出了屈曲约束支撑框架结构的抗震设计方法,张耀春等[13]则对比了普通钢支撑框架与防屈曲支撑框架的抗震性能。研究表明钢支撑束柱构件有别于单榀钢支撑框架结构,主要差别为:单榀支撑框架结构一般柱距较大,故支撑布置形式一般为单斜式、交叉式或人字形(图2(a)),而钢支撑束柱的间距较小,孙建运等[14]对比研究了不同布置方式的钢支撑束柱,认为K形钢支撑束柱相对具有较好的抗侧能力和经济性(图2(b))。
为确保钢支撑束柱有较好的抗震性能,其设计准则为:束柱中钢支撑应先于束柱中的梁柱屈服而屈曲。通过3组相同尺寸的2层单跨钢支撑束柱试件,测试试验模型的受载变形全过程及其整体承载性能,并研究:1)钢支撑束柱在单调水平荷载作用下的极限承载力、刚度和稳定性;2)钢支撑束柱在水平往复荷载作用下的滞回性能;3)钢支撑对束柱强度、刚度的影响。

图2 单榀框架支撑结构与钢支撑束柱的区别
1 试验概况
1.1 试件设计
钢支撑束柱试件为1∶2缩尺比例模型,各组成部件柱、梁和钢支撑截面形状及尺寸如表1所示,梁、柱钢材为Q345B,支撑的钢材为Q235B。相同的试件有3组,其中,1组试件为单调加载,另外2组为往复加载。组成的钢支撑束柱层高1375mm,跨度为900mm。根据钢结构设计规范[15]的要求,双角钢支撑中间等距设3块填板。梁柱对接焊、钢支撑与节点板角焊缝连接,柱脚与40mm厚底板焊接。
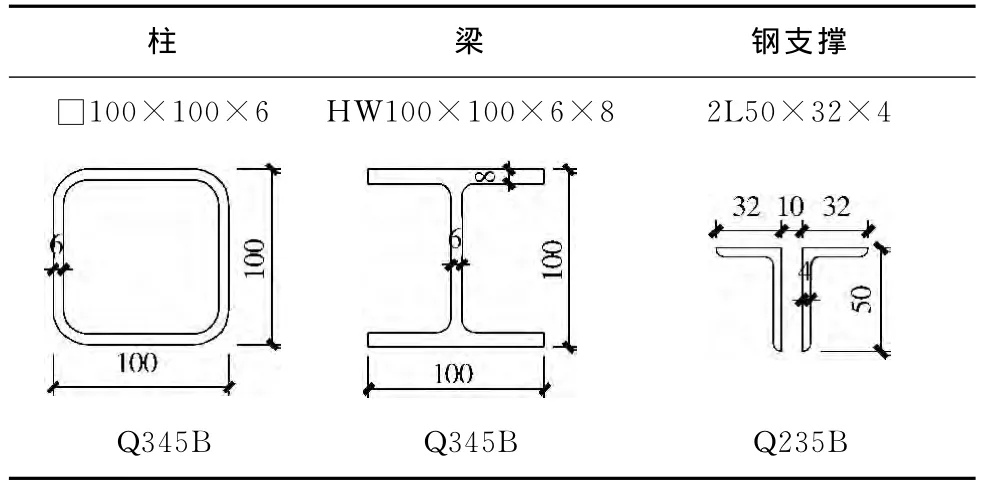
表1 钢支撑束柱组成部件的截面尺寸 mm
1.2 试验装置
钢支撑束柱柱脚用10.9级M24摩擦型高强螺栓与底座固接,底座通过M65锚栓固定在地槽上,约束其竖向变形,同时设置2组水平向圆孔,并利用2根M65水平螺杆约束其水平向位移。为保证束柱试件在水平加载过程中不会发生面外的变形和位移,束柱构件的2根柱面外各设置两榀约束框架(图3)。
试验加载设备采用数控液压作动器,可提供拉力2000kN、压力2000kN,行程500mm,作动器底端与水平反力架相连,顶端与束柱试件连接,底座的水平拉杆与反力架螺栓固接在一起,保证底座与反力架形成自平衡系统。图4描述了水平反力架、液压作动器与束柱试件之间的相互位置关系。

图3 侧向约束框架

图4 水平反力架、液压作动器与钢支撑束柱构件的相互位置关系
1.3 加载制度
预加载采用力控制,±20、±40kN各2次,过程中查看各测点是否正常,确认无误后再开始正式加载。
正式加载时,单调加载,屈服前力控制;屈服后位移控制。往复加载,屈服前力控制;屈服后位移控制,往复加载的具体加载方式如表2所示。
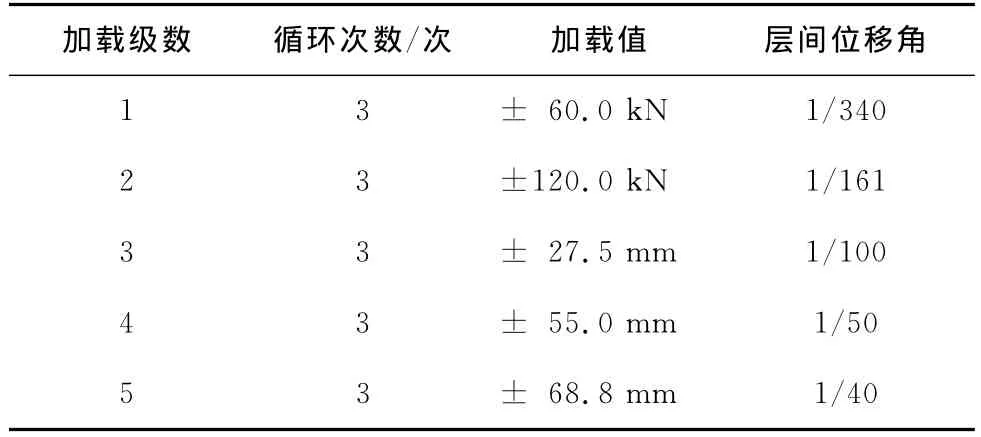
表2 钢支撑束柱往复加载制度
1.4 材性试验
材性试验从柱、梁、内夹钢板和钢支撑中选取材性试件,按照中国标准《金属材料室温拉伸试验方法》(GB/T 228-2002)[15]进行取样及加工。材性试验由国家金属材料质量监督检验中心、上海材料研究所检测中心检测并出具相关性能参数(表3)。
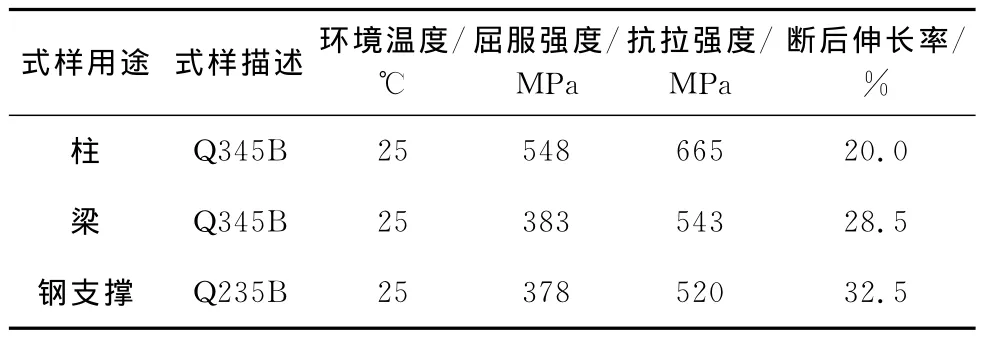
表3 材性试验结果
2 试验结果
2.1 单调加载
试验得到的钢支撑束柱顶层和一层的荷载位移曲线见图5(a)和5(b)。试验曲线开始非常平稳,加载力和位移均匀上升,直至加载到162kN时(层间位移角0.9%),首层受压支撑局部屈曲(图6(a)),并很快发展为整体侧向失稳(图6(b)),束柱承载力突降,但下降至148kN后,束柱承载力又缓慢上升,达到165kN时(层间位移角2%),顶层受压支撑局部屈曲,承载力再一次下降至161kN时该支撑整体失稳(图6(c)),束柱承载力急剧降低,但降至149kN后,束柱承载力再一次上升,但此时2层的受压支撑均已严重破坏(图6(d)),受拉支撑也已屈服,并进入强化段,顶层位移加载至76mm时试验停止。柱脚始终牢固可靠,无任何破坏迹象。
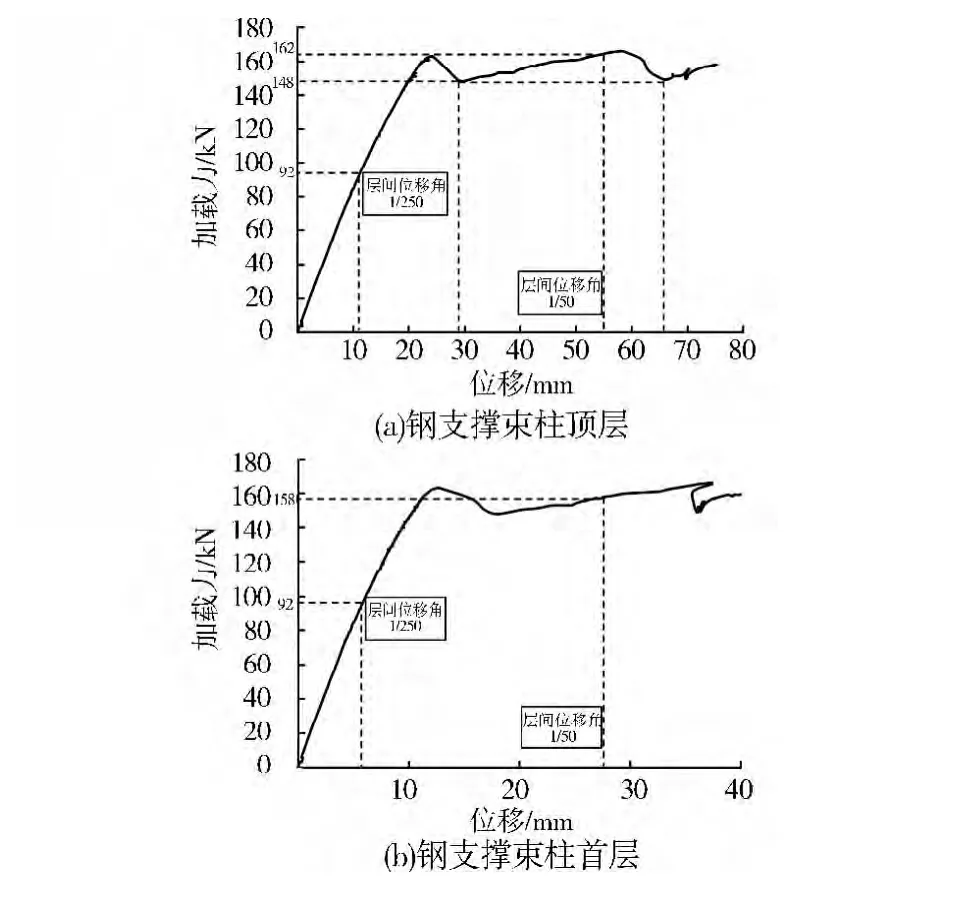
图5 钢支撑束柱荷载位移曲线

图6 钢支撑束柱单调加载试验现象
结合加载破坏过程可知,虽然钢支撑束柱第1次到达极限承载力后首层支撑屈曲,曲线有一个明显的下降段,但它并没有完全退出工作,而且首层受拉支撑仍能够参与受力,随后的曲线也有一个平稳上升段,直到顶层的支撑屈曲破坏,承载力第2次达到极限承载力。曲线的2次“波峰”和“波谷”对应的承载力相差无几,支撑屈曲后束柱承载力的丧失仅为8.6%和9.7%,说明即便受压支撑屈曲,受拉支撑仍可以提供很大的抗侧承载力。
另外,在结构的弹性层间位移角限值1/250时,钢支撑束柱处于完全弹性工作状态;而在弹塑性层间位移角限值1/50时,钢支撑束柱的承载力约为极限承载力的98%,几乎没有下降。
钢支撑受压破坏除整体失稳外(图6(a)、6(c)),还伴随支撑杆件的局部屈曲(图6(d)),支撑肢板宽厚比为12.5,满足规范要求。
钢支撑的长度为,截面参数:A=635.4mm2,ix=15.9mm,iy=15.5mm,
由钢结构设计规范[16],钢支撑的稳定承载力标准值Ncr为:

试验首层支撑屈曲时的应变实测值为ε=1550μ(图7),此时支撑中的内力为:

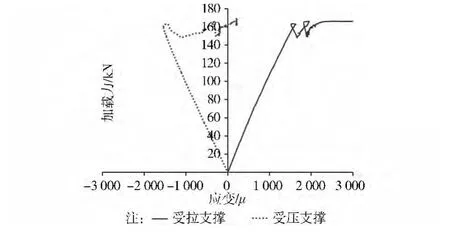
图7 首层支撑加载力应变曲线
由此可见,Ncr≈,说明钢支撑屈曲时的承载力为整体稳定承载力,钢支撑的局部屈曲主要是由于板件塑性变形引起的。
2.2 往复加载
考虑到滞回性能试验的复杂性,安排了2组相同钢支撑束柱试件的滞回性能试验。
相同2组试验构件在相同的试验条件下的结果并不完全相同。图8~9所示钢支撑束柱顶层荷载位移曲线及相应的骨架曲线对比。图10表示钢支撑束柱刚度的退化情况。

图8 钢支撑束柱顶层滞回曲线对比

图9 钢支撑束柱顶层荷载位移骨架曲线对比
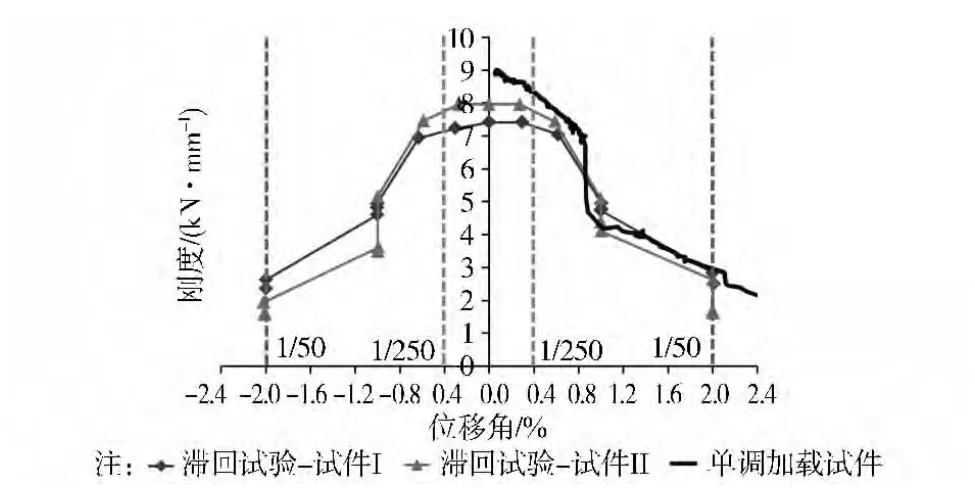
图10 钢支撑束柱刚度退化曲线
试验主要结果如下:
1)钢支撑束柱在各部件截面确定后,其弹性承载力和刚度也即确定。本试验设计的束柱弹性层间位移(17mm,层间位移角1/162)远大于规范[17]要求限值(11mm,层间位移角1/250)。
2)2次试验的破坏过程均为:层间位移角1/100时,底部支撑屈曲;层间位移角1/50时,顶层支撑屈曲;最终,层间位移角1/40时所有支撑全部失效。
3)2次试验在层间位移角1/50前2圈加载时,钢支撑束柱的承载力几乎没有明显下降,但是由于支撑的屈曲,束柱的刚度损失很多。
3 有限元分析与对比
为进一步分析试验结果,采用大型通用有限元程序Abaqus/Standard进行理论对比验证。数值分析的模型尺寸及构造与现场试验一致。
3.1 材料属性
钢支撑束柱各部件均采用壳单元S4R。其中,“S”为通用壳单元,“4”为单元节点数,“R”为单元为减缩积分沙漏控制模式。这种单元为有限应变单元,允许壳在厚度方向尺寸的改变,因此它适合大应变分析,也即它允许壳截面泊松比不为0。
材料本构关系设置为理想弹塑性模型,屈服强度取自各试件材性试验结果,其中梁的屈服强度fy=383MPa,柱的屈服强度f′y=548MPa,钢支撑的屈服强度f″y=378MPa。
3.2 连接接触与约束
梁与柱、梁柱中的加劲肋、钢支撑与节点板以及柱脚与底板的连接,均采用接触关系Tie来模拟实际的焊接,主面与从面相交接触处各节点的平动及转动自由度均耦合。
底板与基础的螺栓连接则近似地约束底板上螺栓对应的点的全部自由度来模拟。同时,约束顶层梁柱节点处的面外变形。
3.3 计算结果与对比分析
建立了该钢支撑束柱的有限元模型,为分析钢支撑对束柱承载力和刚度的贡献,还建立了纯束柱框架的模型,单调加载作用下模型最终破坏形态如图11所示。

图11 钢支撑束柱与纯束柱单调加载的最终破坏
单调加载的荷载位移曲线有限元计算结果跟试验结果十分吻合(图12)。有限元分析采用实际钢材材性试验结果,承载力值非常接近。

图12 钢支撑束柱顶层荷载位移对比曲线
从分析过程来看,首先,束柱首层的受压支撑屈曲造成荷载位移曲线的第1次小幅突降;随后,顶层的受压支撑屈曲再一次造成曲线承载力下降。从图11可见,钢支撑整体失稳的破坏模式与试验基本一致。
需要说明的是,有限元分析的材料本构关系均采用理想弹塑性模型,其分析结果具有很高的精确度,完全不必采用其他更复杂的弹塑性本构关系。可见,对纯钢的结构或构件作分析时,选用理想弹塑性材料本构关系是完全可行的。
现场试验过程中,影响钢支撑束柱构件抗侧刚度的因素有很多,图13中试验开始阶段刚度变化的不稳定与作动器在初始状态下输出力的不稳定以及位移计在微小位移下的精确度不高等问题有关。在顶层的层间位移角达到0.5%以后,有限元的计算结果与试验结果趋于相同。

图13 顶层层抗侧刚度与层间位移角对比曲线
从纯束柱框架的荷载位移曲线对比可知(图12),无论是抗侧刚度还是承载力,框架部分所占比例都非常小。其中,钢支撑束柱达到极限承载力时,纯框架部分只提供14%;而初始抗侧刚度则只占钢支撑束柱的15%。因此,钢支撑束柱绝大部分的承载力和刚度的提供都源自于内部的支撑系统。
钢支撑束柱往复加载时,现场试验以及有限元计算得到的荷载位移骨架曲线与单调加载时的荷载位移曲线的对比如图14所示。可见,有限元计算得到的荷载位移骨架曲线跟单调加载时的荷载位移曲线吻合较好。相比,反复加载试验得到的荷载位移骨架曲线,除了前2级加载3种结果吻合的很好之外,后面几级加载的承载力相比其他2种结果明显降低。这是由于反复加载试验试件存在损伤累积现象,而且支撑在反复荷载作用下屈曲或断裂之后将基本退出工作,从而构件的承载力逐渐降低;但在有限元分析中,钢支撑在某一方向力作用下受压屈曲,但反方向加载时该支撑仍可以参与承受拉力,从而承载力并不会明显下降。

图14 钢支撑束柱顶层荷载位移骨架曲线
4 结论
通过试验和有限元的相互验证,综合研究了钢支撑束柱的抗震性能,得到了这种新型抗侧力构件的承载力、刚度、滞回性能、破坏模式以及简化设计方法。同时,为考察钢支撑对束柱构件承载力及刚度的贡献,还比较了不带钢支撑的纯束柱框架的承载力和刚度。结果表明:
1)钢支撑束柱试验达到了设计目标,即在水平荷载作用下,钢支撑先屈服或屈曲,而梁、柱没有屈曲。
2)钢支撑束柱内部的支撑布置为K型中心支撑,在单调荷载作用下,虽有受压支撑的屈曲,但钢支撑束柱的承载力下降并不大(10%以内),能满足抗侧承载力的需要。因此,钢支撑束柱内的K型支撑布置形式是可行的。
3)钢支撑束柱中,纯束柱框架部分提供的承载力和刚度所占比重很小,分别只有约14%和15%,绝大部分水平剪力都被钢支撑吸收。
4)钢支撑束柱抗侧刚度的退化与内部钢支撑密切相关,一旦支撑屈曲,钢支撑束柱构件的刚度便急剧下降;而钢支撑的整体屈曲源于角钢外伸肢的局部屈曲,外伸肢的宽厚比不应超过规范塑性设计的限值。
5)钢支撑束柱的滞回性能和耗能能力同样与钢支撑紧密相关。在往复荷载作用下,钢支撑局部屈曲部位易断裂,束柱承载力及刚度退化较快。若将普通钢支撑束柱用作结构的抗震构件,则需更严厉地控制钢支撑的宽厚比及填板的焊缝长度。
[1]陆烨.大高宽比屈曲约束组合墙钢框架束柱体系性能研究[D].上海:同济大学,2009.
[2]Astaneh-Asl A,Goel S C.Cyclic in-plane buckling of double-angle bracing [J]. Journal of Structural Engineering,1984,110(9):2036-2055.
[3]Astaneh-Asl A,Goel S C,Hanson R D.Cyclic out-ofplane buckling of double-angle bracing [J].Journal of Structural Engineering,1985,111(5):1135-1153.
[4]Aslani F,Goel S C.Stitch spacing and end fixity in seismic-resisitant boxed angle braces [J].Journal of Structural Engineering,1992,118(10):2872-2889.
[5]Goel S C,el Tayem A A.Cyclic behavior of angle X-bracing[J].Journal of Structural Engineering,1986,112(11):2528-2539.
[6]Xie Q.State of the art of buckling restrained braces in Asia [J].Journal of Constructional Steel Research,2005,61(6):727-748.
[7]Jain A K,Goel S C.Hysteresis models for steel members subjected to cyclic buckling or cyclic end moments and buckling:user’s guide for DRAIN-2D:EL9and EL10,Report UMEE 78R6[R].Ann Arbour(MI, USA): Department of Civil Engineering,University of Michigan,1978.
[8]Ikeda K,Mahin S A.A refined physical theory model for predicting the seismic behavior of braced steel frames,UCB/EERC-84/12 [R].Berkeley,CA,1984.
[9]Tremblay R.Inelastic seismic response of steel bracing members[J].Journal of Constructional Steel Research,2002,58:665-701.
[10]Tremblay R,Archambault M H,Filiatrault A.Seismic response of concentrically braced steel frames made with rectangular hollow bracing members [J].Journal of Structural Engineering,2003,129(12):1626-1636.
[11]Maheri M R,Sahebi A.Use of steel bracing in reinforced concrete frames[J].Engineering Structures,1997,19(12):1018-1024.
[12]Kim J,Seo Y.Seismic design of low-rise steel frames with buckling-restrained braces [J]. Engineering Structures,2004,26(5):543-551.
[13]张耀春,丁玉坤.防屈曲支撑、普通和特殊中心支撑钢框架结构抗震性能分析[J].建筑钢结构进展,2009,11(5):8-15.Zhang Y C,Ding Y K.Seismic response analysis of steel frames braces with buckling restrained,ordinary and special concentrically braces [J].Progress in Steel Building Structures,2009,11(5):8-15.
[14]孙建运,刘青,陆烨,等.钢结构束柱的抗侧性能分析[J].建筑科学与工程学报,2012,29(4):112-119.Sun J Y,Liu Q,Lu Y,et al.Analysis of lateral resistant performance of steel bound-column [J].Journal of Architecture and Civil Engineering,2012,29(4):112-119.
[15]中华人民共和国国家质量监督检验检疫总局.GB/T 228-2002金属材料室温拉伸试验方法[S].2002.
[16]中华人民共和国建设部,中华人民共和国国家质量监督检验检疫总局.GB50017-2003钢结构设计规范[S].北京:中国标准出版社,2003.
[17]中华人民共和国住房和城乡建设部,中华人民共和国国家质量监督检验检疫总局.GB50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.

