PTA氧化反应尾气冷凝系统的数学模拟
黄承明 杨军 何勤伟 李真泽
(中石化上海工程有限公司,上海 200120)
PTA装置的能耗构成中蒸汽占了全部装置公用工程消耗的较大部分。除从界外引入蒸汽外,装置中也具有可以用于产生蒸汽的反应尾气,产生的蒸汽用于透平,以用来驱动装置所需要用的压缩空气。因此,反应尾气冷凝器的优化设计对降低装置能耗具有一定的意义。
本文主要研究如何合理利用PTA氧化反应器尾气的余热,将余热转化为动力蒸汽驱动透平的工况。在PTA的流程中,反应器出料伴较高温度,并具有常排反应器尾气。这些尾气物料中贮存了大量可以被利用的能量,并可以产生副产蒸汽用于透平做功。在既定PTA生产规模中,通过合理的计算可以提高对这股尾气的利用效率,达到冷量回收最优化。
1 研究范围
本文以PTA氧化反应器可凝尾气为研究对象,反应尾气中的余热被多级串联的冷凝器冷却至所需的温度,同时各级冷凝器产生各种不同温度的蒸汽,并利用透平机将蒸汽转化为功。如图1所示。
在PTA的流程中,由于反应器尾气组分为混合物,反应器尾气的焓随温度变化的规律具有一定的拟合关系。拟合后的数学关系在某些温度段内为非线性的关系,这导致了在设置冷凝器的蒸汽侧压力时需要考虑合理性。
2 数学模型的建立
2.1 计算原理
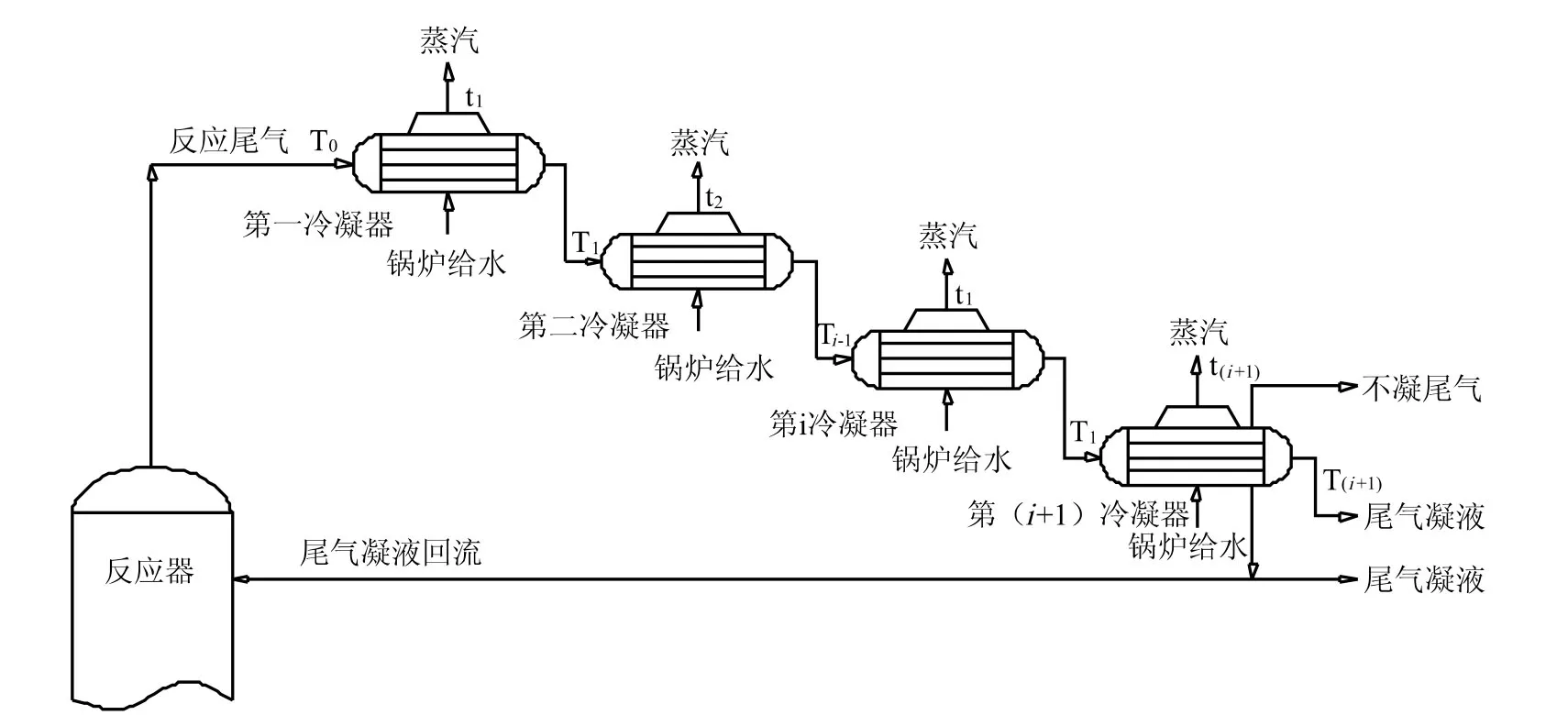
图1 反应器顶部冷凝系统流程
此类问题数学模型主要涉及到两个方面的计算:
一是利用能量守恒的原理,计算蒸汽的产生量。由于尾气的温度为既定值,尾气产生蒸汽的压力不同,对应蒸汽压力下产生的量也随之发生变化。蒸汽压力较高利于透平机做功,但是由于氧化尾气温度为一定值,并且在一定的流量下冷凝到某个温度点只能放出有限的热量,产生高压蒸汽的量就受到影响。这里就存在副产蒸汽压力等级的确定和副产蒸汽量之间的矛盾。引入非线性方程组的目的就是求解此处的矛盾。
二是利用第二定律原理,计算透平机的做功。蒸汽在透平机中做功的能力取决于入口蒸汽的压力和透平机出口状态的压力。蒸汽压力等级越高,做功能力越强。将蒸汽压力等级做功的能力(蒸汽有用能)表示成温度的函数,可以根据温度来判断蒸汽在透平机做功的大小,以此来衡量副产蒸汽在透平机做功的贡献。将此函数引入非线性方程组,作为目标函数对象。
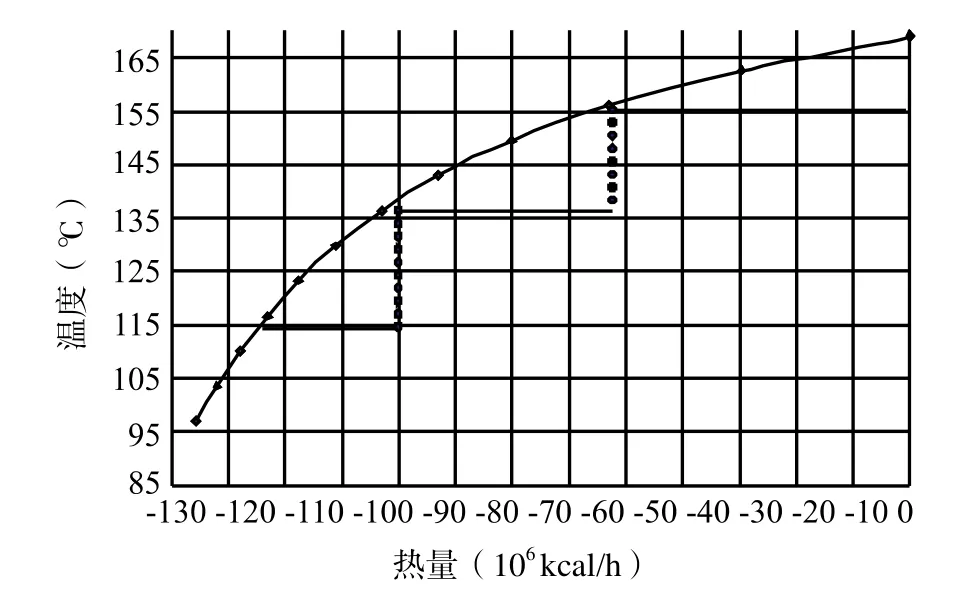
图2 反应器顶部冷凝系统流程
某PTA生产规模的氧化尾气的温焓图如图2,氧化尾气的放热曲线为一条上凸曲线,而非线性关系。从反应器出口到最后一个冷凝器出口的放热量是定值,且冷却到某个温度点能放出的热量也是一定的。如果要最大程度的得到品质较高的蒸汽,就必须在较高的温度位安排换热器回收热量。但是,在较高温度位的时候,由于温度差的关系,能回收的热量的大小受到了限制(即产生蒸汽的量受到限制),如横线所示。横线段的横坐标差值代表这一蒸汽等级所吸收的能量,由此可以推算出此等级下的蒸汽质量,也即能推算出此压力等级下蒸汽能在透平机里做功的大小。因此,关键的变量为副产蒸汽的温度。
在对应的蒸汽压力下,按照这个约束条件,假如安排无穷级能量回收就能最大限度的回收尾气中的能量,但是在现实的工艺过程中是不可能去实现这个过程的。因此,设置间隔一定的副产蒸汽温度差,分段进行有用能的计算,使得结果接近理论上能回收的有用能的大小。
2.2 建立数学模型
2.2.1 反应尾气的温焓拟合关系
不同组分的反应尾气的焓是相对较复杂的数学热力学关系。这种相对复杂的热力学关系是有物质的物理化学性质决定的,即不同尾气温度Ti下各组分的冷凝程度不同。利用温度可以将尾气在第i级换热器的焓表示成数学函数:

式中 Hi— 反应器尾气在对应Ti温度时的焓,kJ/h;Ti— 反应器尾气的温度,℃。
2.2.2 单位质量蒸汽潜热和温度的拟合关系
单位质量蒸汽潜热随温度的变化将发生变化,通过物性手册以及相关的数学拟合方法,能较容易得出蒸汽潜热和温度的函数:

式中 Li— 单位质量蒸汽在对应ti温度下的潜热,kJ/kg;ti— 蒸汽温度,℃。
2.2.3 单位质量蒸汽的有用能和温度的数学拟合关系
有用能是相对的状态函数,把蒸汽进透平机做功后的排放状态的温度作为有用能计算的基态,即(P0,t0)。对于稳流物系,状态1变到状态2,忽略其动能和位能,则单位质量蒸汽做功过程的理想功为:

式中 Wid— 单位质量蒸汽理想功,kJ/kg;
Hi— 单位质量蒸汽焓,kJ/kg;
ti— 蒸汽温度,℃;
t0— 基态蒸汽温度,℃;
Si— 蒸汽熵,kJ/(kg ·℃)。
(i=1,2)
当体系由任意态(Pi,ti)变至基态(P0,t0)时,则上式的Wid的负值就是入口状态物流的有用能:
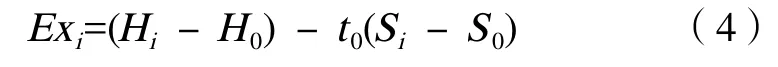
式中 Exi— 单位质量蒸汽相对基态(P0,t0)的有用能,kJ/kg;
Hi— 单位质量蒸汽焓,kJ/kg;
ti— 蒸汽温度,℃;
t0— 基态蒸汽温度,℃;
Si— 单位质量蒸汽熵,kJ/(kg ·℃)。
S0— 基态下单位质量蒸汽熵,kJ/(kg ·℃)。
(i=1,2)
为了计算方便,可以将任意态(Pi,ti)蒸汽温度段内相对基态(P0,t0)的有用能拟合成蒸汽温度ti的函数:

式中 Exi— 单位质量蒸汽相对基态(P0,t0)的有用能,kJ/kg;
ti— 蒸汽温度,℃。
3 数学模型的建立
假设第i级冷凝器产生的蒸汽温度为ti,并且锅炉给水为饱和水,则第i级冷凝器产生的蒸汽质量为:

式中 mi— 第i级冷凝器产生的蒸汽质量,kg/h;
Hi— 反应器尾气在对应Ti温度时的焓,kJ/h;
Li— 单位质量蒸汽在对应ti温度下的潜热,kJ/kg。
假设第i级冷凝器产生的蒸汽温度为ti,则第i级冷凝器产生的蒸汽质量拥有的总有用能exi为:

式中 exi— 第i级冷凝器产生的蒸汽质量所拥有的总有用能,kJ/h;
Exi— 单位质量蒸汽相对基态(P0,t0)的有用能,kJ/kg;
假设,反应器冷凝级数有i级,则冷凝工段的总有用能可以表示为:

式中 ex — 冷凝器工段产生的蒸汽质量所拥有的总有用能,kJ/h;
exi— 第i级冷凝器产生的蒸汽质量所拥有的总有用能,kJ/h。
在既定的PTA产品规模下,为了获得最多的有用能用于透平机组,则要求总有用能ex最大化,可以表达成非线性规划方程组:
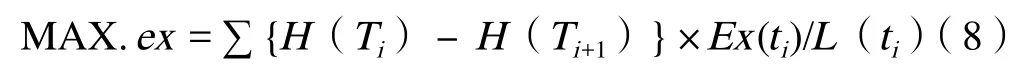
此方程组需要设置边界条件才有物理意义。
4 数学模型边界条件的确定
方程(8)是一个非线性规划方程,为了解出其具有物理意义的结果,需要添加合理的边界条件进行约束。边界条件是由此流程的特点所决定。其中包括如下的几个具体方面:
(1)第i级冷凝器的尾气出口温度等于第i+1级的入口温度。
(2)第i级冷凝器的出口温度比第i级蒸汽温度相差一定值,用△Ti来表示,则第i级冷凝器的尾气出口温度Ti和第i级冷凝器的发生蒸汽温度ti的数学关系为:△Ti=(Ti-ti)。△Ti的大小取决于冷凝器的制造成本,成本越低,△Ti可以越小。
(3)由于发生蒸汽需要一定的温差,△Ti的大小应小于(Ti-1-Ti)的值。
故,带约束的非线性方程为:
MAX. ex=∑{H(Ti)-H(Ti+1)}×Ex(ti)/L(ti)(9)
S.T.
△Ti≥ 0;
△Ti≤(Ti-1-Ti)。
值得注意的是,为了规定流程的范围,往往规定最后一级冷凝器的出口温度,再利用上述的方程组进行求解。
5 计算举例
5.1 流程描述
某工艺PTA装置的氧化反应器的反应温度为186℃,压力为12.1 bar(1 bar = 0.1 MPa)。反应器顶部尾气在169.2 ℃,11bar的条件下排放。利用换热器可以将反应尾气冷却至一定温度,并同时产生低压蒸汽。氧化反应器顶部尾气出来后直接进入到第一冷凝器的管程进行冷却冷凝,第一级氧化反应器的管程侧,第一冷凝器的壳程侧通入锅炉给水,进行热交换后产生低压蒸汽。整个冷凝过程分有四级冷凝器,冷凝的部分凝液返回至氧化反应器进行再利用。
反应器顶部出口尾气的温度为169.2 ℃的饱和气体混合物,物料组成见表1。

表1 尾气物料组成
这股尾气进入到冷凝器中将被部分冷凝,此过程的放热量将是气、液两相的显热差和液相部分气化潜热的加和。
5.2 流程数学模型的建立
5.2.1 反应尾气的温焓拟合关系
有关文献[1-2]对这个过程的热力学提供了一套可靠的研究方法,借助Aspen Plus软件则可以得到这股尾气的温焓非线性的拟合方程:
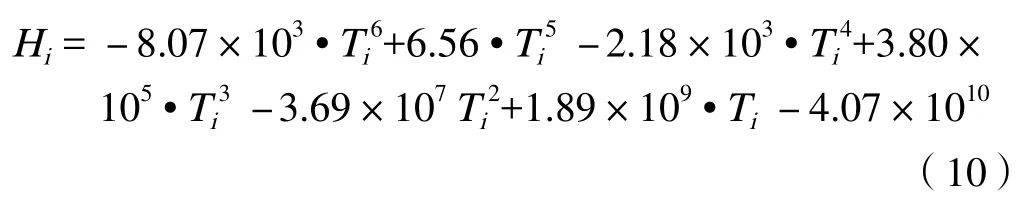

表2 蒸汽有用能表
R2=0.999 9,(97 ℃,169.2 ℃)
式中 Hi— 反应器尾气在对应Ti温度时的焓,kJ/h;
Ti— 反应器尾气的温度,℃。
5.2.2 单位质量蒸汽潜热和温度的拟合关系
根据文献[3]中水蒸汽的物性,可以查到水在对应的温度下的汽化潜热的大小,并通过拟合成如下的关系式L= HL(T):

式中 Li— 单位质量蒸汽在对应ti温度下的潜热,kJ/kg;
ti— 蒸汽温度,℃。
5.2.3 单位质量蒸汽的有用能和温度的数学拟合关系
根据有用能的计算方法,设定透平机出口的状态为基态(如表2中,-0.9S的参数),计算各个压力等级下的相应的有用能如表2所示:
根据表2的结果,可以拟合如下有用能关于温度的函数关系Exi=Ex(ti):

式中 Exi— 单位质量蒸汽相对基态(P0,t0)的有用能,kJ/kg;
ti— 蒸汽温度,℃。
5.2.4 数学模型的建立
此PTA流程中冷凝器系统发生蒸汽的温度可以通过下列方程求得:

i=1,2,3,4。
6 数学模型的求解结果
6.1 四级换热求解结果
将上述方程通过数学软件求解(如,Matlab,Lingo等软件),计算结果没有出现边界值,可以作为此模型的最优解。计算结果如下表3。

表3 氧化反应尾气冷凝系统蒸汽温度计算结果
计算结果显示,此流程中四级冷凝器产生的蒸汽压力等级呈现散点分布,最终获得了较高的有用能。四级换热器的总有用能为1.277×109kJ/h。
在实际装置中,为了考虑设备造价等因素的影响,往往牺牲有用能回收量来减少设备投资。某PTA工艺装置的四级冷凝器的设计数据见表4。
通过比较实际运行参数可以发现,装置设计参数和计算结果相差不大,总有用能的回收量为1.239×109kJ/h,为表4中计算值的97%。考虑设备造价等因素,装置实际运行时牺牲了3%的能量回收量。同时发现,第二冷凝器的负荷相对较小,使得换热器负荷分布不成规律。
6.2 三级换热求解结果
为了深入探讨此系统的冷凝器的设置方法,本文计算了三级冷凝器的工况。计算结果如表5。
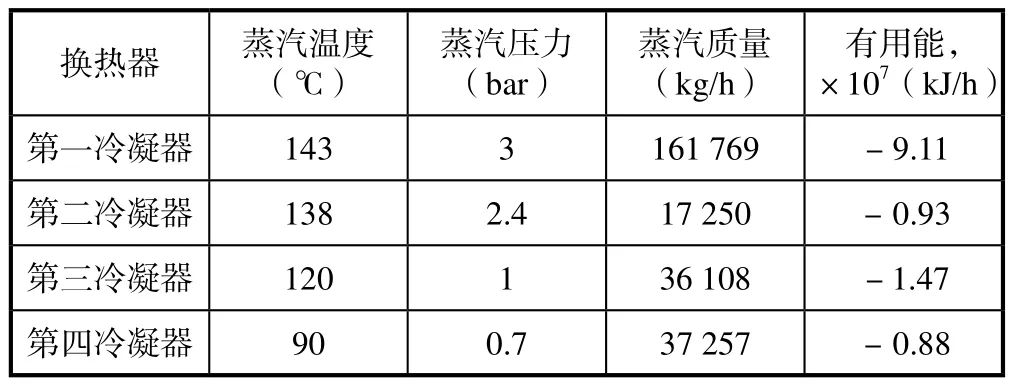
表4 氧化反应尾气冷凝系统蒸汽温度运行数据

表5 氧化反应尾气三级冷凝系统蒸汽温度计算
三级冷凝器能回收的总有用能为1.274×109kJ/h,接近四级冷凝器串联回收的总有用能1.277×109kJ/h,相对量相差大约0.3%。并从数据中发现,三级换热器回收的总有用能分布较合理,设计冷凝器时冷凝器面积逐减,即使三级冷凝器也可以达到较好的能量回收效果,三台冷凝器的设置在设备布置等方面具有一定的优势。
7 结果分析
利用带约束的非线性方程求解PTA氧化反应器尾气冷凝系统的蒸汽发生温度的问题可以得到较合理的计算结果。通过某工艺PTA装置的设计参数和计算结果对比,发现本文的计算结果与设计数据相仿,回收的总有用能不小于设计数据。
以某个PTA产品规模的氧化冷凝器尾气回收为例,计算了三级冷凝系统蒸汽发生温度,并与四级冷凝系统的参数比较。结果表明,三级冷凝系统也能达到较好的能量回收效果,可以作为设计此类系统的设计参考依据。
工程实际中,往往需要引入设备造价、设备维修费用等其它边界条件,因此,本文的计算具有一定的局限性,需要完善。在工程设计时,可以在以上的计算结果的基础上考虑设备投资、设备制造、设备维护以及厂区内蒸汽平衡的现状来设计数学模型的边界条件,使得计算结果更具有工程意义。
8 结论及展望
本文使用非线性规划方法对PTA氧化反应器尾气冷凝系统进行优化计算,详细描述了数学模型的建立以及求解情况。利用某产品规模的PTA氧化尾气冷凝器系统的参数建立数学运转模型为例题,阐述计算过程。通过参数对比,证明此方法在此类问题上具有很好的参考价值,可以作为系统初步数据设置的依据。
利用非线性规划问题优化时,各个冷凝器的蒸汽温度可以通过带约束条件的非线性规划方程一次求解,可以根据不同的约束条件进行设置边界条件或评价标准[4],例如:可把有用能或蒸汽价格作为优化目标等,来获得不同侧重点的边界条件下的计算结果。边界条件也可以考虑设备的形式、制造难度、运输、吊装及检修等费用。另外,由于模型的建立是基于膨胀机出口状态的情况而建立起来的,膨胀机的设计对模型也有很大的影响。
[1] 何勤伟,杨军,蔡军杰. PTA氧化反应器顶部冷凝器的优化设计[J]. 石油炼制与化工,2006,37(11):53-57.
[2] Hayden J G, O’Connell J P. A generalized method for the predicting second virial coefficients[J]. Ind Eng Chem Process Des Dev,1974,14(3): 209-216.
[3] 姚平经. 全过程系统能量优化综合[M]. 大连:大连理工大学出版社,1995.
[4] 陈钟秀,顾飞燕,胡望明. 化工热力学[M]. 北京:化学工业出版社,2001.

