基于发动机性能的传感器故障隔离方法研究

朱大明

（中航空天发动机研究院，北京100028）

0 引言

在发动机工作和试验中，其实际物理过程状态量是经过传感器采集输出，成为测量数据，然后再进入监控和诊断系统。由测量数据显示的故障现象是由发动机部件产生的，还是由传感器产生的，这对监控与诊断有效性将产生很大影响，所以判断传感器是否有故障、隔离及辨识故障就显得很重要。目前，在传感器故障诊断领域常用的方法主要有神经网络[1]、主元分析[2]（PrincipalComponentAnalysis）、卡尔曼滤波[3]和小波分析[4]等方法，但这些方法很难应用在研制阶段的发动机试验故障诊断中。

本文以发动机性能模型为基础，借助模型自适应性和模式识别技术，建立多种以分析发动机性能参数偏差来模拟测量参数偏差的传感器诊断方法。

1 整机试验传感器故障特点

对于研制阶段的发动机整机试验，其传感器故障有3个特点：（1）测取的参数经常变化，每次试验测取的参数不同。在台架试验阶段，发动机测量参数虽然较多，但是由于调整和串装的原因，试验测取的参数种类容易发生变化，对于同1台份的发动机，在同1试验台架上的多次试验所得到的可能是1组种类不同的测量参数。（2）测量参数记录不完整。对于研制阶段的发动机，由于未知因素多，可靠性不高，易出现突发问题；再加之受试验发动机寿命、试验部件寿命和试验任务等各种因素的影响，在1次试验中，所记录的或可用的测量参数可能只有少量几组，甚至只有1组。（3）处于研制阶段的发动机缺乏传感器故障模式及实际故障案例的积累[1]，无从获得“历史稳态数据”和“时间序列数据”。

基于以上几点，在传感器故障诊断领域常用的方法很难适用。

基于发动机性能模型，借助模型自适应性和模式识别技术建立了多种以分析发动机性能参数偏差来模拟测量参数偏差的传感器诊断方法。这些方法不限定固定的测量参数序列，不需要随时间变化的数据序列和历史稳态数据序列，在只有1组测量参数序列的情况下就可以使用。并且对发动机本身发生故障时，隔离传感器故障效果良好，尤其适用于在发动机多故障并发的情况。

2 发动机总体性能仿真模型的建立

本文在传感器故障诊断隔离的研究中建立了1个双轴分排涡扇发动机性能仿真模型。该仿真模型除了变比热、非线性、部件级以外，还充分考虑可调部件调整和各部件经验修正系数对发动机性能的影响，能十分方便地设置发动机试验可调参数和所需的经验修正系数，并对其进行调节。因试验调整而引起的性能及其主要参数变化，能方便地通过修正部件特性，将基线模型自适应到试验发动机。

首先建立气体热力性质函数求解模型，包括定压比热、焓、熵、气体常数和气体绝热指数等，均为自变量为油气比和温度的多项式拟合[8]；然后采用焓熵法依次计算各部件出口气流参数[8]；最后求解共同工作点，试取1组参数，联合已知参数进行沿流路各部件的气动热力计算，利用共同工作条件作为检查方程，反复迭代，直到满足收敛条件[9]。具体过程如图1所示。在图中，左侧圆角框为已知条件，上侧方框为试验参数，下面等式方框为平衡方程，AL 为辅助线位置，N1为高压相对物理转速，H 为飞行高度，Ma 为飞行马赫数，A 为喷管喉部截面积，L 为功，q 为折合流量，pi 为涡轮膨胀比，下角标I和II分别为内涵与外涵，c为计算值，d 为设计值，m 为特性图上值。

图1 共同工作点求解过程

发动机总体性能模型建立以后，使用发动机真实试验数据对模型进行校核。设真实发动机设计数据为DA，模型计算值为DC，非设计点的校核结果如图2所示。在图中，πFan为风扇压比，wazhFan为风扇折合流量，F 为推力，nzhHPC为高压压气机折合转速。从图中可见，建立的发动机性能模型具有较高精度。

图2 发动机非设计点校核结果

3 传感器故障隔离方法

3.1 发动机自适应模型

在进行传感器故障隔离前，首先建立发动机自适应模型。若分别用Y、X、V 表示测量参数、特性参数和可调参数向量，则发动机性能模型可表示为Y=FEPS(X,V)。当可调参数不变时，性能模型可表示为Y=FEPS(X)。发动机自适应模型就是当发动机实际测量参数与设计值或基线值不相同时，可以依据对测量数据的分析结果对发动机部件特性进行微调，将发动机总体性能数学模型自行修正到反映试验发动机实际状态的数学模型。若用FEPS.ad表示自适应运算，发动机自适应模型可表示为X=FEPS.ad(Y)。求解的方法是：在可行取值范围内，给出多个X，通过FEPS计算对应的Y，直到某个Xc计算得到的Yc与实际测量参数Ya满足事先给定的相似条件SIM()，则认为此时的Xc就是发动机部件特性实际值Xa。若用相对欧拉距离度量相似性，则求解自适应模型X=FEPS.ad(Y)可以表示为如下优化问题

式中：dcor.Y为Yc和Ya的相对欧拉距离；ΓY、ΓX分别为测量和故障参数向量中各分量的取值可行域。

3.2 传感器故障隔离计算方法

基于发动机性能模型的传感器故障隔离方法基本原理是：设发动机试验可以得到m个测量参数，利用m个测量参数可以通过发动机自适应模型来估计发动机的性能，m个测量参数对应着m个传感器。诊断过程是，针对每个测量参数，每次都使用除了这个参数本身以外的m-1个测量参数估计发动机性能。以第i个测量参数yi为例，使用除第i个测量参数yi以外的的其余测量参数通过发动机自适应模型估计发动机性能。如果是第i个传感器发生了故障，那么只有这次得到的性能估计结果是正确的，因为它没有使用发生故障传感器的测量信息。而其余的m-1次估计，由于都使用了第i个传感器得到的测量参数yi，即都使用了故障传感器的测量参数信息，所以得到的性能估计结果都会不同程度地偏离实际情况。这样就可以隔离故障传感器。

上述基本原理相当于1个通用方法，包括了2个主要方面：（1）获得被进行传感器故障检测的发动机的当时性能，即发动机本身是否存在故障，若有故障，故障程度是多大；（2）采用有效的性能自适应模型。基于此，可以得出下述多种实际传感器隔离算法。

3.2.1 发动机本身无故障情况（简称方法1）

若发动机本身无故障，则直接考察m 次，用m-1个测量参数自适应得到的性能参数向量Xi（i=0~m）与基线性能XBA的差异（相对平方距离Si）即可，最接近基线性能的1组（Δi=min{Si,i=1…m}），其序号i 对应的传感器即为故障传感器。实际在传感器故障隔离之前，无法确定发动机本身是否有故障。下面研究未知发动机故障的情况下隔离传感器故障的方法。

3.2.2 发动机本身也有故障（简称方法2）。

若发动机本身有故障，则在传感器故障隔离前，不知道发动机的故障部件和故障程度，此时无法获得发动机真实性能。在这种情况下，对于通用方法可做如下修改，仍然以第i个测量参数yi为例。步骤是：（1）对于测量参数yi，优化其取值，使得对于这组测量参数Y，用包括yi在内的m个测量参数通过发动机自适应模型得到的性能参数最接近无故障基线值的性能参数向量XBA。本文此处设定，通过优化测量参数yi得到的最接近XBA的性能参数向量为Xi，二者之间的差异为Si。对每1个测量参数都这样进行优化取值，然后使用自适应模型进行自适应计算，则可以得到m个Xi和Si；（2）直接使用m个测量参数，通过发动机自适应模型可以得到1组性能参数向量，设为X0，和XBA的差异设为S0；（3）考察Si（i=1~m）与S0之差，差别最大的1组（Δi=max{(S0-Si),i=1…m}），取值被优化的测量参数i 对应的传感器即为故障传感器。

如果存在传感器故障，则直接用m个测量参数估计的发动机性能不准确，而与之相差最大的1组是因为优化了某个测量参数yi的取值。所以其自适应得到的结果与包含故障传感器的自适应结果相差最大，这个测量参数yi对应的第i个传感器就是故障传感器[10]。其计算流程可参考文献[11]。

3.2.3 方法1、2的比较讨论

有效的发动机性能自适应模型是上述方法的基础。从数学角度出发，判断自适应程度的优劣，实际上是考察自适应结果状态向量与自适应目标状态向量之间的相似程度。在可调参数不变的情况下，这里所说的状态向量既可以是测量参数向量也可以是性能参数向量。方法1就是选择了测量参数向量，方法2选择的是性能参数向量。

上述方法隔离的标准都是考察自适应模型结果性能参数Xc与目标性能参数Xg之间的差异，均使用相对平方距离S=Σ(xc/xg-1)2。在自适应目标值都是基线值的情况下，即Xg=XBA，方法1的数值实质是寻找m个Si中最小的1个，即min{Si}；方法2的数值实质是寻找m个Si与S0之间差的最大的1个，即max{S0-Si}，相当于min{Si}。方法2中依次对每个测量参数进行优化，改变其取值，并最后寻找距离差异最大，其原理实质是寻找哪个测量参数对错误信息影响最大；而方法1则是寻找哪个测量参数对正确信息影响最小。这2种方法殊途同归。

3.2.4 发动机故障未知下的新方法（方法3）

方法1是针对无故障发动机，相当于已知实际发动机性能，即基线性能；方法2虽然未知发动机实际性能，但是以基线发动机性能为过渡目标值，以基线性能参数为自适应目标进行了传感器故障隔离。对于1次发动机试验，得到的只有测量参数，下面建立了1个以测量参数为自适应对象，并针对发动机实际性能未知情况下的传感器故障隔离方法。以第i个传感器得到的测量参数yi为例。使用除yi以外的m-1个测量参数进行自适应。若yi是故障传感器得到的测量参数，则本次自适应就没有使用到故障信息，在自适应模型较为准确的条件下，应该能匹配到某个发动机真实物理工作状态，设此状态为UK（unknown）状态，则用来自适应的测量参数向量与UK状态的测量参数向量之间的相对欧拉距离为

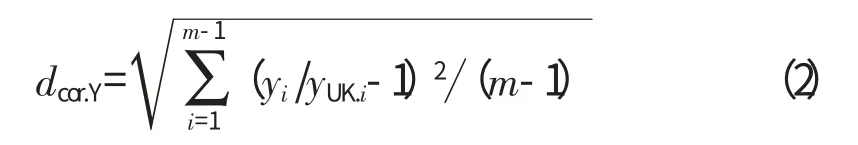
在理论上dcor.Y=0，实际计算中存在收敛精度ε，dcor.Y也为一小量，且dcor.Y≤ε。

若yi不是故障传感器得到的测量参数，则本次自适应使用到了故障信息，在自适应模型较为准确的条件下，无法匹配到任何发动机真实物理工作状态，即使真实测量参数向量与某个状态测量参数向量之间的距离dcor.Y满足收敛精度ε，也是个相对较大的数值。

所以直接使用自适应收敛的判断量dcor.Y就可以进行传感器故障隔离。这种方法显然也适用于发动机本身无故障的情况。取m个dcorY.i中的最小值，即Δmin=min{dcorY.i,i=1~m }，此时Δmin对应的测量参数yi即为故障传感器得到的测量信息，第i个传感器即为故障传感器。

3.2.5 发动机故障对传感器隔离的影响

无论是传感器故障，还是发动机故障，都要体现在测量参数的变化上。而且从试验中也只能得到测量参数。由此可认为，发动机本身故障的测量参数，实际上影响了传感器故障在测量参数上的体现。若把这种影响的程度定义为ADETS(Affect Degree,Engine To Sensor)，则显然在传感器故障程度一定的情况下，发动机故障程度越低，ADETS越小，就越容易分辨出传感器故障。而随着发动机故障程度的增加，ADETS也增大，在测量参数序列中分辨传感器故障也难。所以事实上，无论哪种传感器故障隔离方法，在发动机故障程度严重时，其准确度都会降低。上述方法在自适应模型准确度降级时，故障隔离有效性程度会下降。当发动机本身故障程度严重时，自适应模型的准确度就会随之降低，导致传感器故障隔离有效度也会降低。对此可以考虑应用加权的方法来增强故障隔离的效果。

3.2.6 传感器故障加权隔离方法

当发动机本身故障较为严重，隔离有效性降低时，可做加权处理，设传感器测量精度为qi，则权重系数wi显然可以表示为qi的某种函数，此时考察加权距离(widcor.Yi)即可。这样的加权方法虽然符合权重的思想，但在传感器故障隔离时不适用。因为不知是哪个传感器发生故障，倘若权值大的传感器恰好是故障传感器，则这样的加权不仅没有起到增大区分度的作用，反而增大了故障信息对隔离的影响，使隔离效果变得更差，甚至出现错误隔离。对于研制阶段的发动机整机试验，没有传感器历史稳态数据，也没有大量的时间序列数据，所以本节采用的加权方法不是精度加权，而是“稳定性”加权。即对于某次试验，首先默认1个或多个传感器无故障，然后在自适应过程中，以这个或这些个测量参数为收敛检验参数，以故障可能性低、较为稳定的测量参数作为加权考虑参数，此称之为“稳定性”加权。如：推力和转速测量出现故障的可能性很低，则可以把这2个参数作为收敛检验参数。本章上述算法的自适应收敛标准是2个测量参数向量之间的相对欧拉距离dcorY小于等于收敛精度ε。当稳定性加权时，不仅要考察向量整体的接近程度，还要考虑加权参数的接近程度，设推力和低压转速的收敛精度为εFn和εNf，则加权前后的自适应收敛目标为

加权前

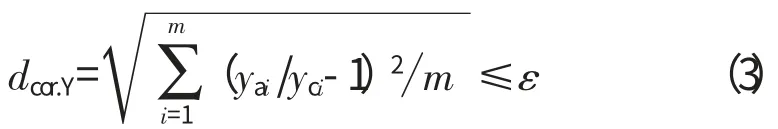
加权后

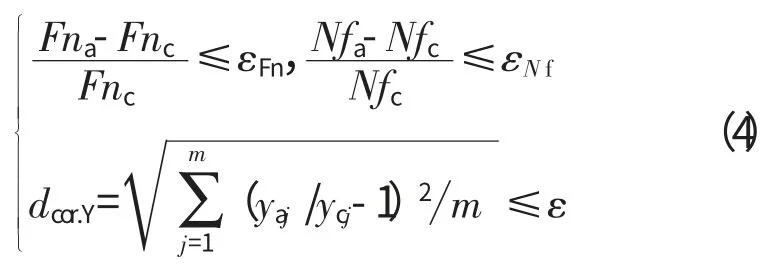
由此可以改善传感器故障隔离区分度。但是由上述对ADETS的叙述可知，即使使用了这样的加权隔离方法，与发动机本身无故障情况相比，其隔离的有效程度仍会有所降低。

3.3 传感器故障隔离应用

以1个双轴分排涡扇发动机为例，采用上述方法，对传感器故障隔离进行数值仿真。该发动机的测量参数设为发动机地面台架试验所取，只针对在发动机故障诊断及其他数据分析中起到重要作用的2个测量参数，即高压压气机出口总温T3和低压涡轮出口总温T55进行数值模拟试验。测试案例由发动机性能仿真模型模拟产生。为了更加接近真实试验情况，在模型的模拟计算得到的测量参数序列中加入了随机噪声。计量实践表明，对于等精度测量，随机噪声落入（μ±3σ）范围的概率为99.73%，μ、σ 分别为每种测量参数的平均值和方差。所以m 种测量参数yi对应的随机噪声noise.yi=R(μi+3σi)。R 为区间[-1,+1]之间符合均匀分布的1个随机数。

本文只针对发动机有故障时的传感器故障隔离进行仿真。首先设置发动机故障，发动机故障情况远比传感器故障情况复杂。本文选择2种故障情况：（1）压气机故障，流通能力下降2%，效率降低0.02；（2）压气机故障和外涵道故障并发，压气机流通能力下降2%，效率降低0.02，外涵总压恢复系数下降4%。选择这2种典型故障都是在建模过程中对应的真实发动机和在研制阶段整机台架试验的真实故障。

首先计算压气机故障时传感器故障隔离。使用方法2、3在发动机双故障情况下，计算压气机和低压涡轮出口总温传感器故障的隔离，结果如图3、4所示。

图3 发动机双故障测量有噪声隔离结果（方法2）

图4 发动机双故障测量有噪声隔离结果（方法3）

从图3中可见，方法2已经出现了无法隔离的区域，而方法3的隔离效果依然良好。当发动机故障更加严重时，方法2的隔离效果更差，分析意义不大，所以只研究方法3，其计算结果如图5所示。

图5 发动机3故障测量有噪声隔离结果（方法3）

从图5中可见，当发动机故障较为严重时，方法3隔离效果也变差，出现较大的无法隔离区域，根据前文所述，采用“稳定性加权”的方法，认为推力和低压转速传感器无故障，其收敛精度均为测量精度的1.2倍。再次计算，得到的隔离结果如图6所示。

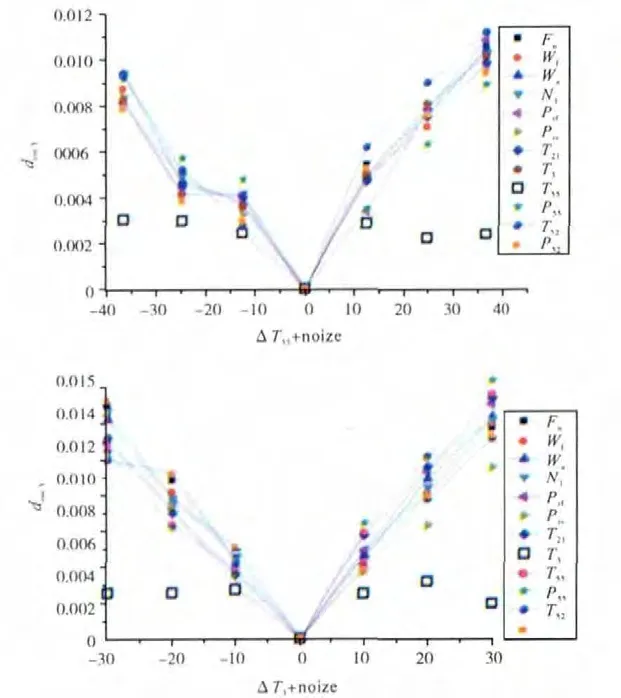
图6 发动机3故障测量有噪声隔离结果（方法3）

从图6中可见，虽然有些故障程度下的效果较差，但已经可以隔离，只是区分度不高。前文已述，发动机故障会影响传感器故障在测量参数中的表现，即使采用加权的方法，也只能改善隔离效果，不能完全解决区分度不好的问题。

4 结论

（1）考察故障参数自适应结果与目标故障参数相似程度S，取其中最小值（min{Si}）对应为故障传感器。

（2）考察故障参数自适应结果与基线故障参数相似程度S 之间的差Δ，取其中最大值（max{Δi=S0-Si}）对应为故障传感器。

（3）考察自适应收敛判断量dcor.Y，取其中最小值（min{dcor.Yi}）对应为故障传感器。

（4）对2个主要故障传感器进行的各种算法的应用研究分析结果表明，采用dcor.Y作为隔离指标，隔离效果最为良好。

[1]张洪生.基于模式识别的航空发动机燃油控制系统传感器故障诊断[J].航空发动机，2008，34（2）:43-45.ZHANG Hongsheng.Fault diagnosis of fuel control system sensor for aeroengine based on pattern recognition[J].Aeroengine,2008,34（2）：43-45.(in Chinese)

[2]孙涛，李本威，李忠东，等.人工神经网络在某型航空发动机故障诊断中的应用[J].航空发动机，2004，30（3）：52-55.SUN Tao,LI Benwei,LI Zhongdong,et al.Application of ANN technology to aeroengine fault diagnosis[J].Aeroengine,2004,30（3）：52-55.(in Chinese)

[3]YE Zhifeng,SUN Jianguo.Simulation investigation of aeroengine fault diangosis using neural networks[J].Transactions of Nanjing University of Aeronautics& Astronau,2001（2）：157-163.

[4]龚志飞，郭迎清.基于主元分析法的航空发动机传感器故障诊断研究[J].计算机测量与控制，2012，20（8）：2017-2020.GONG Zhifei,GUO Yingqing.Investigation of aeroengine sensor fault diagnosis based on principal component analysis[J].Computer Measurement&Control,2012,20（8）：2017-2020.(in Chinese)

[5]俞刚，黄金泉.基于支持向量机和卡尔曼滤波器的航空发动机故障诊断研究[J].航空发动机，2012，38（1）：47-51.YU Gang,HUANG Jinquan.Aeroengine fault diagnosis based on support vector machine and Kalman Filter[J].Aeroengine,2012,38（1）：47-51.(in Chinese)

[6]孙涛，侯志强，张赟.基于小波包分析和案例推理的转子系统故障诊断方法[J].航空发动机，2010，36（1）：27-31.SUN Tao,HOU Zhiqiang,ZHANG Yun.Rotor system fault diagnosis based on wavelet packet analysis and CBR[J].Aeroengine,2010,36（1）：27-31.(in Chinese)

[7]李一波，张宗杰，蒋丽英.航空发动机故障诊断信息融合方法研究现状[J].航空发动机，2009，35（3）：36-40.LI Yibo,ZHANG Zongjie,JIANG Liying.Development of information fusion methods for aeroengine fault diagnosis[J].Aeroengine，2009，35（3）：36-40.(in Chinese)

[8]廉筱纯，吴虎.航空发动机原理[M].西安：西北工业大学出版社，2005：152-165.LIAN Xiaochun,WU Hu.Aeroengine principle[M].Xi'an：Northwestern Polytechnical University Press,2005：152-165.(in Chinese)

[9]申功璋，高金源，张津.飞机综合控制与飞行管理[M].北京：北京航空航天大学出版社，2008：143-152.SHEN Gongzhang,GAO Jinyuan,ZHANG Jin.Aircraft integrated control and flight management[M].Beijing：Beihang University Press,2008：143-152.(in Chinese)

[10]Kurzke J.Sensor checking using model based engine performance test analysis and numerical optimization[R].ISABE-2005-1239.

[11]朱大明，朱之丽.航空发动机整机试验性能故障诊断系统设计[J].航空发动机，2011，37（4）：43-48.ZHU Daming,ZHU Zhili.Aeroengine overall test performance fault diagnosis system design[J].Aeroengine,2011,37（4）：43-48.(in Chinese)

[12]彭靖波，谢寿生.Elman回归神经网络在航空发动机故障诊断中的应用[J].航空发动机，2007，33（2）：46-48.PENG Jingbo,XIE Shousheng.Application of Elman neural network in aeroengine fault diagnosis[J].Aeroengine，2007，33（2）：46-48.(in Chinese)

[13]包睿，黄金泉.航空发动机反馈神经网络自适应控制方法[J].航空发动机，2007，33（4）：46-49.BAO Rui,HUANG Jinquan.Adaptive control method for recurrent neural network of aeroengine[J].aeroengine，2007，33（4）：46-49.(in Chinese)

[14]王永华，李本威，孙涛，等.基于部件特性自适应的涡扇发动机仿真[J].航空发动机，2009，35（2）:20-23.WANG Yonghua,LI Benwei,SUN Tao,et al.Self-adaptation simulation of turbofan engine based on components characteristics [J].Aeroengine，2009，35（2）：20-23.(in Chinese)

[15]潘慕绚，黄金泉.航空发动机模型参考自适应控制综述[J].航空发动机，2003，29（2）：51-54.PAN Muxuan,HUANG Jinquan.Summary of model refrence adaptive control of aeroengine[J].Aeroengine，2003，29（2）：51-54.(in Chinese)