磁悬浮轴承系统的时滞动力学建模与控制研究
郑 凯
(中航工业沈阳发动机设计研究所,沈阳110015)
0 引言
磁悬浮轴承是利用可控磁场力提供无接触支承而使转子稳定悬浮于空间的1种高性能轴承,具有高转速、无需润滑、工作温度范围广及可测可控性好等诸多优点[1],目前在空间技术、物理学、机械加工、振动控制、机器人、离心机、膨胀机等诸多工业领域中得到广泛应用[2-4],且作为新一代多电航空发动机转子的主要支承方式,引起世界各国研究机构和学者的高度关注[5-13]。磁悬浮轴承转子系统在高速、超高速下运行时,会受到结构材料强度、动力时滞、锥型涡动、电压电流钳制等诸多因素的影响和限制,其中时滞的影响最不可忽略。机电控制系统中的时滞在数值上很小,一般只有几十微秒,在系统相对简单、时滞环节不多且对于系统动力行为无严格限制的情况下,忽略其产生的效应并没有什么不妥。但对于工作在苛刻条件下的复杂机电系统,考虑到航空发动机等重要设备的高可靠性要求,其设计技术和控制理论研究必须构筑在更加严密的体系框架基础上,必须认真考虑时滞的作用。特别对于在高速环境下运转的磁悬浮轴承系统而言,即使是数字控制系统中的微小时滞,与转子的转动周期在数量级上也已经相当接近,因此有可能对转子系统的稳定性和动态性能产生很大影响,必须加以细致研究。目前,对于磁悬浮轴承时滞问题的研究已经引起了一些关注[14-19],但大都仅限于简单的单自由度系统的动力学问题,且在高速转子系统控制的问题上却很少考虑时滞的影响。
本文建立了时滞反馈下的5自由度磁悬浮轴承机电耦合的动力学模型,对时滞影响下的磁悬浮轴承系统的镇定控制律进行研究。
1 系统时滞动力学建模
在实际中,磁悬浮轴承-转子系统可以视作1个5自由度刚性转子系统,如图1所示。其径向由2个径向磁轴承支承,轴向由1个推力轴承支承。
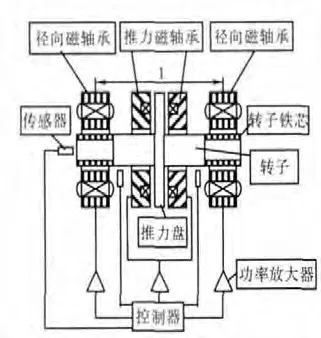
图1 5自由度磁轴承-转子系统

图2 转子受力情况
转子受轴承电磁力情况如图2所示。转子径向2支点a、b 之间的跨度为l,转子质心O 距左右支点的距离分别为la、lb。设转子在2个支点处的广义坐标qB=[xayaxbybzc]T,则转子系统的运动微分方程可写作[20]
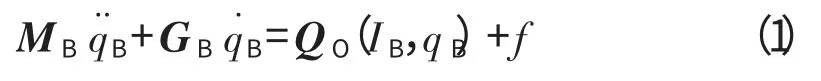
其中

式中:m 为转子质量;Jox、Joy为转子的赤道转动惯量;Joz为转子的极转动惯量;Joxz、Joyz为转子的转动惯量积;ω 为转子的角速度;f 为不平衡扰动项;Qo为磁悬浮轴承所提供的动态力和力矩。
将上式线性化可得
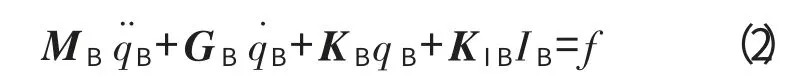
式中:IB为控制电流;KB和KIB的数学表达在文献[1]中给出,在此不作赘述。
上述运动方程都是不封闭的,电流IB需要由反馈控制系统提供。反馈控制系统主要由传感器、控制器和功率放大器等组成,由传感器检测获得转子的位移信息后送入控制器,在控制器中经过控制运算得到控制信号后送入功率放大器,功率放大器根据控制信号产生相应的控制电流电磁铁形成电磁力,使转子保持在平衡位置。反馈控制系统的传递函数如图3所示。
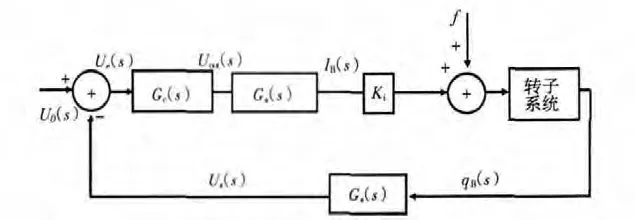
图3 磁轴承-转子系统的控制传递函数
在图3中,Gs(S)为传感器传递函数,可视作1阶环节

式中:As为传感器的增益系数;Ts为传感器的衰减时间常数。Gc(s)为控制器传递函数,以PD控制器为例,则有

式中:kp,kd分别为控制器的比例系数和微分系数。
功放环节的传递函数Gc(s)也可视作1阶环节

式中:αa为功率放大器的增益系数;Ta为功率放大器电路的衰减时间常数。
以往对于磁悬浮轴承转子系统的研究,大多在同一时间的参考系下展开,而实际上反馈回路中各环节的工作,如传感器中位移信号采集、处理与转换以及控制器中控制算法的运算等,都不可避免要消耗一定的时间;此外,执行单元中功率放大器的饱和效应和电磁铁线圈中的涡流损耗和磁滞特性,也可能造成一定的迟滞效应[14]。将控制系统各部分的时滞考虑在内,则系统的传递函数如图4所示。在图4中所加入时滞的来源见表1。
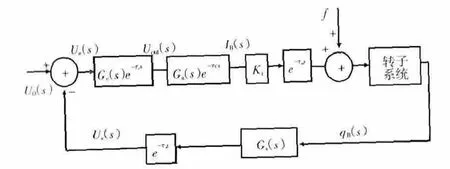
图4 计入时滞后的磁悬浮轴承-转子系统的控制传递函数

表1 各部分时滞的来源
取控制的参考输入为U0=0,将式(3)~(5)分别写成微分方程形式,与式(2)联立可以得到考虑时滞反馈磁悬浮轴承系统的机电耦合微分方程组

式中:Kp,Kd为控制器增益矩阵。
Kp,Kd可根据需要设计。若选用式(4)中PD控制器,则Kp,Kd皆为对角阵,可表示为
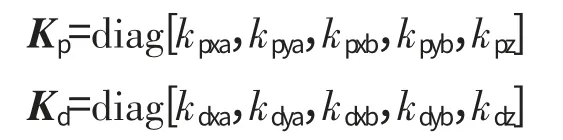
矩阵中的系数为对应自由度上的比例和微分系数。下面将给出考虑反馈时滞后控制增益阵的确定方法。
2 镇定控制器设计
对于磁悬浮轴承转子系统,假定其传感器和功率放大器均工作在线性区域,取Ta=0,Ts=0,τ=τa+τc+τs+τm,则式(6)可简化为
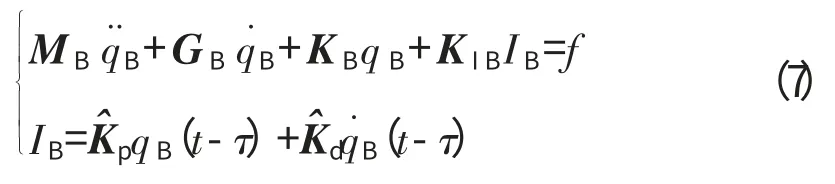
写成状态方程为
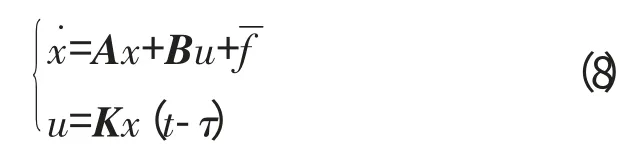
磁悬浮轴承系统属于高速动态系统,反馈回路中的各时滞项都是随时间变化的,因此,本文将时滞τ用有界时变函数表示为
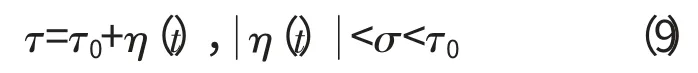
τ0和σ 都为常数,可通过对反馈回路中时滞进行测算来确定,则有τ(t)∈[τ0-σ,τ0+σ]。对于系统方程式(8),采用Lyapunov直接法可以推导出以下命题。
假设τ0,σ 和μ 为给定正参量,且满足τ0>σ,μ>0,如果存在矩阵使得下列线性矩阵不等式成立

系统在反馈时滞满足τ(t)∈[τ0-σ,τ0+σ]的情况下可由控制输入u=Kx(t-τ)镇定,控制增益为

假定存在矩阵Q>0,R1>0,R2>0,N=[N1N2],P=
将式(8)写作描述子系统
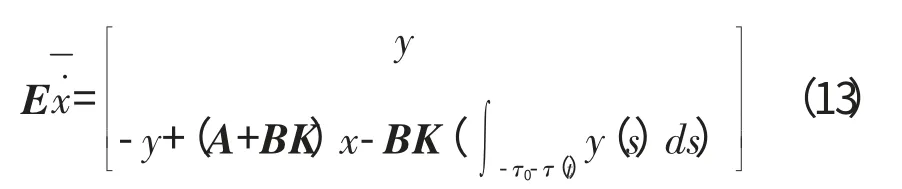
构造Lypunov函数
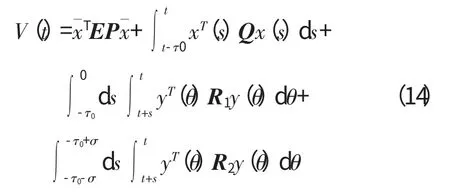
对V(t)求导,并利用以下2个不等式[21-22]放大。
(1) 对 于 任 意a∈ℜn,b∈ℜ2n,N∈ℜ2n×n,R∈ℜn×n,Y∈ℜn×2n,Z∈ℜ2n×2n,则有
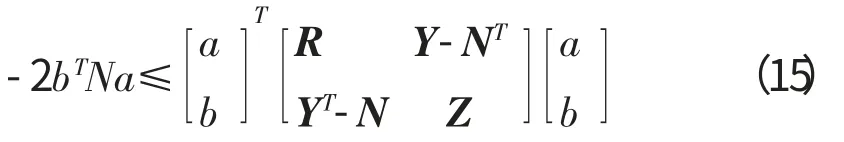
其中

(2)对于任意向量a,b 和正定对称矩阵Λ,则有
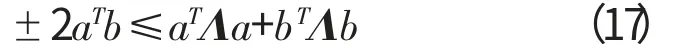
得到不等式

其中ξT=[xT(t),yT(t),xT(t-τ0)]

由Lyapunov定律可知,系统渐进稳定的充分条件为

对式(19)应用Schur补性质[17]进行矩阵变换后,令左乘和右乘diag{X X X X},并引入变量变换则可以得到式(10)。同样对式(16)采取相似变换可以得到式(11)。前文命题得证。
定理将系统镇定控制问题转化为线性矩阵不等式问题,利用内点法[21]求解式(11)和(12),可以确定时滞相关的状态反馈控制器的增益阵K。
3 仿真分析
选取一实际的磁悬浮轴承刚性转子系统为对象,其参数值见表2、3。

表2 磁悬浮轴承转子系统参数(转子部分)
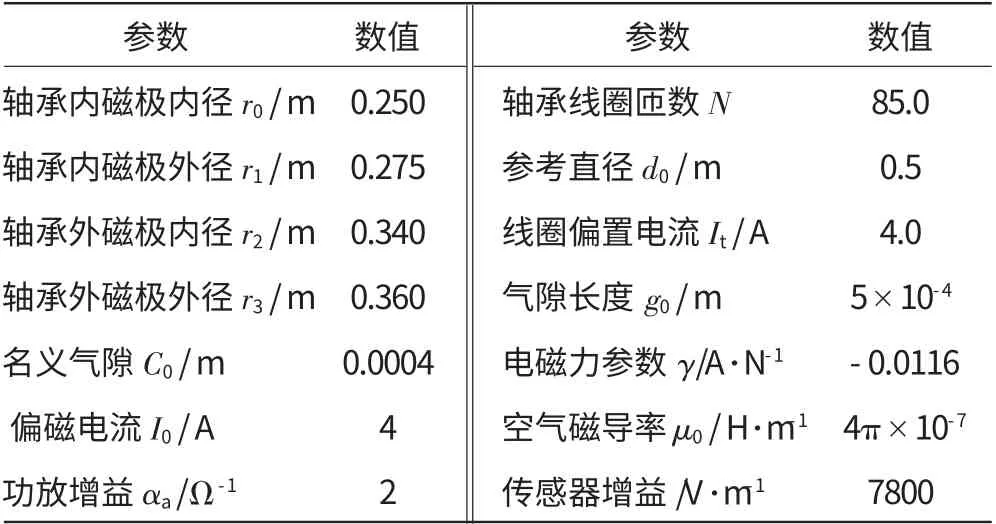
表3 磁悬浮轴承转子系统参数(轴承部分)
3.1 时滞对系统的影响
首先选用式(3)未考虑时滞的PD控制器进行仿真,在xa、ya、xb、yb自由度上分别采用独立的PD控制,其控制参数为
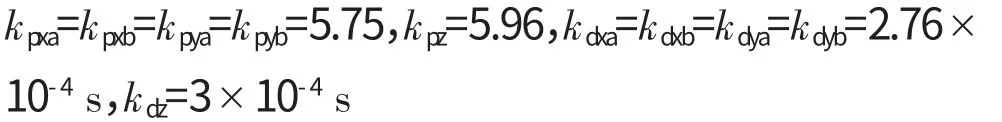
设转子工作转速为20000r/min,为研究时滞对系统的影响,对式(6)在以下2种情况下进行仿真计算。
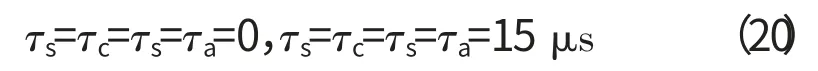
加入时滞前后转子a侧与轴向的振动情况分别如图5、6所示。
从图5、6中可见,PD控制器在假定系统不存在时滞的情况下时可以保持转子系统稳定,且控制性能尚可;但在反馈回路中计入总计60μs时滞后,系统出现剧烈振荡,并最终失稳。这表明在控制反馈回路中即使存在微秒级的微小时滞,但已经对高速转子系统的动态特性和稳定性产生重大影响,使得动态性能变差,甚至出现失稳。

图5 无时滞,PD控制器仿真结果
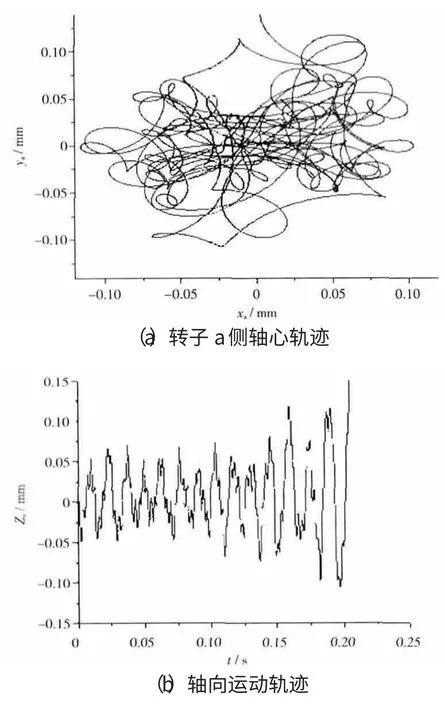
图6 计入时滞后,PD控制器仿真结果
3.2 镇定控制算法验证
将表1、2中的参数代入状态方程式(8),依据定理,取μ=0.1,可以求得满足式(10)和(11)的控制增益
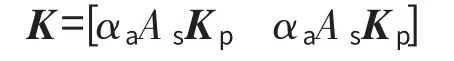
其中

将Kp、Kd代入式(9)后,与3.1节中对PD控制器的仿真研究相同,依然在假定系统无时滞和计入时滞2种情况下进行仿真运算,计入时滞前后转子的振动情况如图7、8所示。
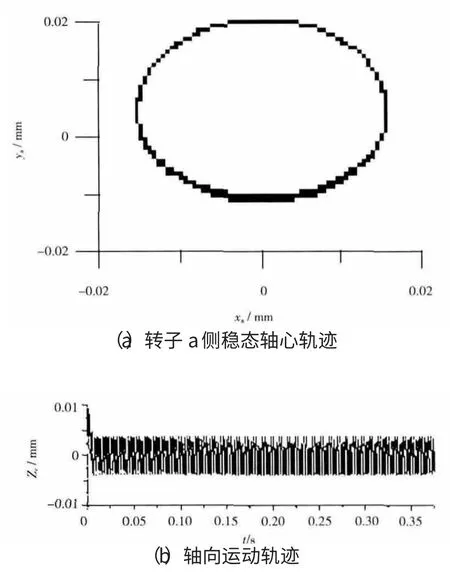
图7 无时滞,本文设计的控制器仿真结果

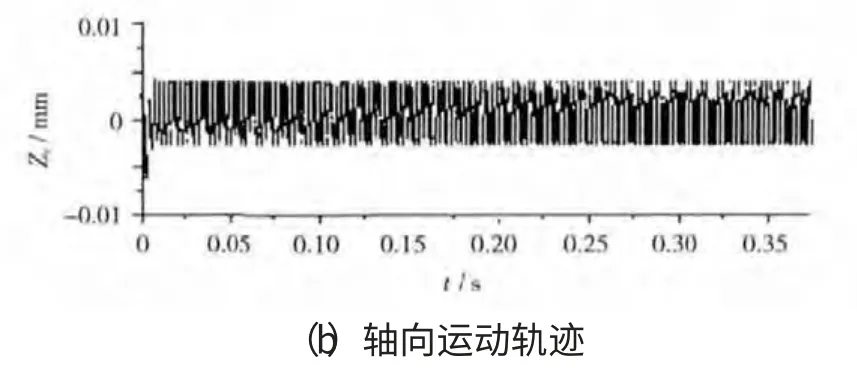
图8 计入时滞后,本文设计的控制器仿真结果
经过镇定算法可以看出转子系统在计入反馈时滞后,没有出现类似PD控制器一样失稳的状况,动态性能并未发生明显变化,依然可以稳定运行,控制算法的有效性得到验证。
4 结论
(1)由于在机电系统中微秒级的时滞已经可以影响到高速转子系统的动力学特性。因此在该系统动力学和控制研究时,应该考虑时滞效果。
(2)通过适当的控制方法,可以有效地抑制时滞对系统的负面效果,保证转子系统稳定运行。
(3)对高速转子系统稳定性的理论方法和数值计算方法的研究除时滞外,应将其他多种非线性因素(如不平衡扰动,电磁线圈的涡流影响)等考虑在内,研究多种因素对于转子系统动态特性的综合影响。
(4)研究能够较为精确的测量实际机电系统中时滞的方法,为系统稳定性和控制设计提供有力的支撑和依据。
(5)对时滞控制理论研究,需要进一步降低控制器设计中的保守性,并提高控制器对于模型不确定性和扰动的鲁棒性。
[1]虞烈.可控磁悬浮转子系统[M].北京:科学出版社,2003:2-3.YU Lie.Controlled magnetic levitation system [M].Beijing:Science Press,2003:2-3.(in Chinese)
[2]Schweitzer G,Bleuler H,Traxler A,et al.Active magnetic bearings:theory,design,and application to rotating machinery[M].Heidelberg:Springer-Verlag,2009:2-10.
[3]Dussaux M.The industrial applications of the active magnetic bearing technology [C]//Proceeding of 1st International Symposium on Magnetic Bearings.Tokyo Japan:NISSEI Eblo,1990:33-38.
[4]Brunet M.Practical applications of the active magnetic bearings to the industrial world [C]//Proceeding of 3rd International Symposium on Magnetic Bearings.ETH Zurich:Springer,1988:225-244.
[5]汪希平,谢建华,朱礼进.电磁轴承在航空发动机应用中的设计问题分析[J].航空发动机,2002(1):4-8.WANG Xiping,XIE Jianhua,ZHU Lijin.Analysis in design problems of AMB applied in aircraft engines[J].Aeroengine,2002(1):4-8.(in Chinese)
[6]常春江,杨荣.电磁轴承及其应用(第一部):分电磁轴承的发展及其应用前景[[J].航空发动机,2003,29(1):46-49.CHANG Chunjiang,YANG Rong.Application of AMB,Part I:development and prospects of active magnetic bearing in aeroengine[J].Aeroengine,2003,29(1):46-49.(in Chinese)
[7]常春江,杨荣.电磁轴承及其应用(第二部分):电磁轴承工作原理和设计要点[J].航空发动机,2003,29(2):44-50.CHANG Chunjiang,YANG Rong.Application of AMB,PartⅡ:fundamentals and design of active magnetic bearing in aeroengine[J].Aeroengine.2003,29(2):44-50.(in Chinese)
[8]杨荣,常春江,龚学耕.电磁轴承系统的试验研究[J].航空发动机,2001(4):15-19.YANG Rong, CHANG Chunjiang, GONG Xuegeng.Experimental and design of active magnetic bearing in aeroengine[J].Aeroengine,2001(4):15-19.(in Chinese)
[9]张钢,汪希平.实验用航空发动机磁悬浮轴承样机的稳定性分析[J].航空发动机,2002(2):1-5.ZHANG Gang,WANG Xiping.Stability analysis of experimental AMB prototype for aircraft engine [J].Aeroengine,2002(2):1-5.(in Chinese)
[10]XU L,WANG L,Schweitzer G.Development of magnetic bearings for high temperature suspension[C]//Proceeding of 3rd International Symposium on Magnetic Bearings.ETH Zurich:Taylor&Francis Group,2000:117-122.
[11]Mekhiche M,Nichols S,Oleksy J,et al.50 KRPM,1100°F Magnetic Bearings for Jet Turbine Engines[C]//Proceeding of 3rd International Symposium on Magnetic Bearings.ETH Zurich:Taylor&Francis Group,2000:123-128.
[12]Kelleher W P,Kondoleon A S.A magnetic bearing suspension system for high temperature gas turbine applications[C]//Industrial Conference and Exhibition on Magnetic Bearings.Virginia:Technomic Pub.Co,1997:15-24.
[13]Storace AF.Integration of magnetic bearings in the design of advanced gas turbine engines[J].Journal of Engineering for Gas Turbines and Power,1995,117:655-665.
[14]Inoue T,Ishida Y.Nonlinear forced oscillation in a magnetically levitated system:the effect of the time delay of the electro-magnetic force[J].Nonlinear Dynamics,2008,52(Compendex):103-113.
[15]JIANG W,WANG H,WEI J.A study of singularities for magnetic bearing systems with time delays[J].Chaos,Solitons and Fractals,2008,36(Compendex):715-719.
[16]WANG H,LIU J.Stability and bifurcation analysis in a magnetic bearing system with time delays[J].Chaos,Solitons and Fractals,2005,26(Compendex):813-825.
[17]Wang H,Jiang W.Multiple stabilities analysis in a magnetic bearing system with time delays[J].Chaos,Solitons and Fractals,2006,27(Compendex):789-799.
[18]JI J C.Stability and hop bifurcation of a magnetic bearing system with time delays[J].Journal of Sound and Vibration,2003,259(4):845-856.
[19]JI J C.Dynamics of a Jeffcott rotor-magnetic bearing system with time delays[J].International Journal of NonLinear Mechanics,2003,38(9):1387-1401.
[20]张钢,李松生,张建生,等.磁悬浮轴承-转子系统的机电耦合动力学模型[J].机械科学与技术,2003(增刊1):46-49.ZHANG Gang,LI Songsheng,ZHANG Jiansheng,et al.Coupled electrome-chanical dynamic model of rotor-magnetic bearings system [J].Mechanical Science and Technology for Aerospace Engineering,2003(S1):46-49.(in Chinese)
[21]Moon Y S,Park P,Kwon W H,et al.Delay-dependent robust stabilization of uncertain state-delayed systems [J].International Journal of Control,2001,74(14):1447-1455.
[22]CAO Y Y,SUN Y X,Lam J.Delay-dependent robust H∞control for uncertain systems with time-varying delays[J].IEE Proceedings:Control Theory and Applications,1998,145(3):338-344.
[23]Boyd S,Ghaoui L E,Feron E,et al.Linear matrix inequalities in system and control theory[M].Society for Industrial and Applied Mathematics,1994:115-130.

