桩间距对双排式钻孔抗滑桩的影响研究
温祥虎,叶四桥,2,毛晓光
(1.重庆交通大学 水利水运工程教育部重点实验室,重庆 400074;2.重庆市地勘局,重庆 400074;3.武汉市政工程设计研究院,武汉 430023)
0 引言
目前,治理推力较大的滑坡,当使用单排抗滑桩难以有效支档或结构受力不合理时,可以采用双排抗滑桩.为探讨双排抗滑桩受力特性,一些学者为此进行了研究分析.熊治文等[1],何颐华等[2],杨明辉等[3]等进行了双排抗滑桩实验研究;王成华等[4],王乾坤[5],韩爱民等[6],张建勋[7],周德培等[8]等进行了抗滑桩桩间距和土拱效应研究分析;毛晓光[9],黄小艳等[10]等对双排抗滑桩桩间距进行了初步的研究分析.然而以上学者基本上是对单排桩或者桩顶无连接双排抗滑桩进行的研究,而对机械钻孔的桩顶有连接的双排抗滑桩还有待于进一步研究.尤其是现阶段在推力较大的滑坡的治理中,探索性采用具有施工安全、速度快、节省成本等优点的双排式钻孔抗滑桩时,有必要搞清楚桩间距对双排式钻孔抗滑桩的影响规律.
本文采用有限元程序ABAQUS 建立双排式钻孔抗滑桩的有限元三维分析模型,其它条件不改的情况下,分别改变模型中桩间距,进行单因素分析.利用有限元分析计算结果,并以桩顶位移、桩身弯矩最大值、桩身剪力最大值和前后排桩承担滑坡推力的比例为分析指标,分别作出不同桩间距下关系曲线图,探讨其影响规律,确定其较优的桩间距范围,从而为双排式钻孔抗滑桩设计和施工提供参考依据.
1 有限元分析模
1.1 基本假定
(1)滑坡岩土体本构模型采用Drucker-Prager模型,滑床岩土体本构模型采用Mohr-Coulomb 模型;由于抗滑桩主要承受水平推力结构,所以抗滑桩的桩身采用线弹性实体梁单元模型,承台也采用线弹性实体梁单元模型.
(2)边界条件:为了模拟实际工作状态下抗滑桩的受力,根据实际受力条件设置计算范围内模型的边界条件.滑坡体模型的滑床底部加三向约束,滑床左右两侧以及前后缘也加三向约束,为保证滑体不从左右两侧面边界挤出,滑体左右两侧面加水平方向约束,滑体后边界方向施加水平方向约束,滑体前缘面不加约束,以便滑体反翘剪出,坡顶、坡面和坡脚均不加约束.
(3)桩和土相互作用界面不考虑相对滑动,在接触界面上采用Goodman 无厚度单元定义摩擦接触面,在接触面上共用有限元网格节点,以满足变形协调条件.
(4)承台与前后排桩采用刚结点连接,可以传递弯矩和剪力.滑坡推力通过桩和岩土体的相互作用传递到抗滑桩上,滑坡推力在前后两排桩上分担,主要通过前后两排桩与承台及桩间土体的共同作用实现.
1.2 材料参数
1.2.1 模型尺寸
在相同的滑坡条件下,建立双排式钻孔抗滑桩的有限元三维分析模型(见图1),桩长16 m,桩径为d=1 m,滑动面以上10 m,嵌入滑床6 m,桩间距S,排间距4 m,承台高度为1.5d,后排桩处滑体厚度为10 m,滑面的倾角0°,在后排桩后留5 m 岩土体处,为模拟滑坡推力,在滑体后表面竖向加40 kN/m的水平均布载荷.前后排桩分别建立5 根桩,多取前后排桩最中间一根桩进行桩身的位移和内力分布及两排桩承担荷载比例分析.模型纵断面示意图见图2.
为便于文章陈述,作如下规定:首先承担滑坡的推力且位于滑坡后部的排桩为后排桩;则位于滑坡前部另一排桩为前排桩.

图1 有限元分析模型

图2 双排式钻孔抗滑桩的纵断面
1.2.2 模型材料参数
模型桩身与承台钢筋混凝土采用强化拉伸塑性应力-应变的等效钢筋混凝土[11],抗拉强度fc=2.4 ×106Pa,抗压强度fc=2.4 ×107Pa.模型的基本物理力学参数见表1.

表1 模型的物理力学参数
2 桩间距的影响数值模拟结果分析
在ABAQUS 中建立双排式钻孔抗滑桩的有限元三维分析模型,在滑体推力、排间距、桩长、桩径等滑坡条件不改的情况下,变动模型中桩间距S,S分为2d、3d、4d、5d、6d 进行单因素分析.对有限元计算的结果进行分析,并以桩顶位移、桩身弯矩最大值、桩身剪力最大值和前后排桩承担滑坡推力的比例为分析指标,作出不同桩间距下关系曲线图,分析结果如下:
2.1 桩间距对桩顶位移的影响
不同桩间距与桩顶位移关系曲线如图3 所示,桩顶位移的变化受桩间距的影响很明显,桩顶位移和桩间距呈现正相关性,随着桩间距增大,桩顶位移增大.表明,在确定的排间距时,随着桩间距增大,而每延米的滑坡推力不变,每根桩承担滑坡推力成正比例增大,桩顶位移也随之增大,直到桩间距过大滑坡土体从桩间挤出,双排抗滑桩失效.
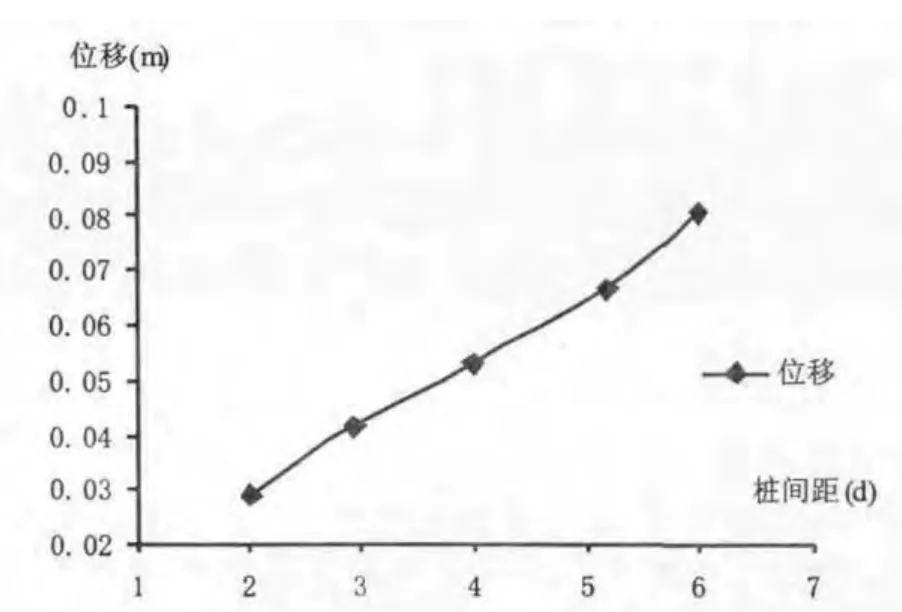
图3 桩间距与桩顶位移关系图
2.2 桩间距对桩身弯矩的影响
不同桩间距与前后排桩桩身弯矩图分别如图4、5 所示,由图知,随着桩间距的变化,前后排桩桩身弯矩最大值位置基本不变,前后排桩桩身弯矩分布变化很小,而对桩身弯矩最大值影响明显.不同桩间距与前后排桩的桩身弯矩最大值得关系曲线如图6 所示,分析可得,随着桩间距的增大,前后排桩的桩身弯矩最大值增大,呈现正相关性.表明,在确定的排间距时,随着桩间距增大,而每延米的滑坡推力不变,每根桩承担滑坡推力成正比例增大,桩身最大正弯矩值和桩顶负弯矩值明显增大,直到桩间距过大滑坡土体从桩间挤出,双排抗滑桩失效.
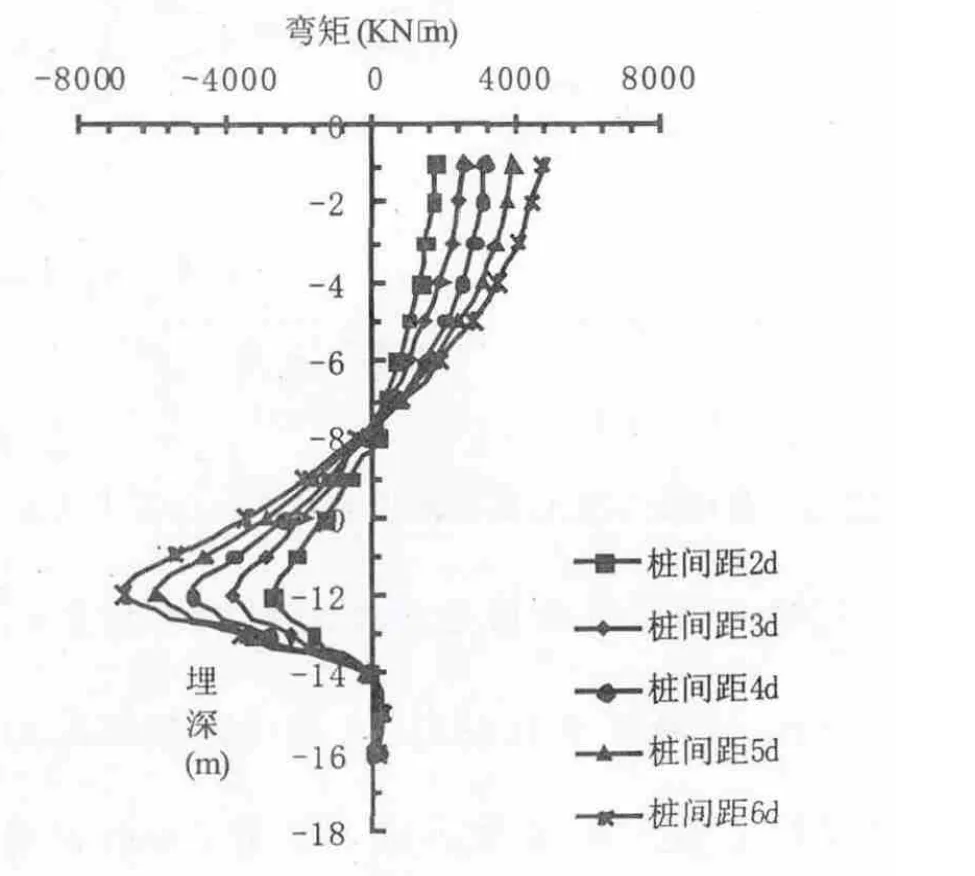
图4 前排桩桩身弯矩图

图5 后排桩桩身弯矩图

图6 桩间距与桩身弯矩最大值关系图
2.3 桩间距对桩身剪力的影响
不同桩间距与前后排桩桩身剪力图分别如图7、8 所示.

图7 后排桩桩身剪力图

图8 前排桩桩身剪力图
由图知,随着桩间距的变化,前后排桩桩身剪力最大值位置基本不变,前后排桩桩身剪力分布变化很小,而对桩身剪力最大值影响明显.不同桩间距与前后排桩的桩身剪力最大值得关系曲线如图9所示,分析可得,随着桩间距的增大,前后排桩的桩身最大剪力值增大,呈现正相关性.表明,在确定的排间距时,随着桩间距增大,而每延米的滑坡推力不变,每根桩承担滑坡推力成正比例增大,桩身最大剪力值和桩顶剪力值明显增大,直到桩间距过大滑坡土体从桩间挤出,双排抗滑桩失效.

图9 桩间距与桩身剪力最大值关系图
2.4 桩间距对前后排桩承担推力比例的影响
对于桩身,土体的变形引起的桩后的土压力就是滑坡推力;对于圆形桩,将桩周法向土压力分解换算成滑坡推力方向上的力,乘以作用范围内的面积,就是桩所承担的推力[9].定义荷载分担比例:为前排桩或者后排桩所承担的荷载占前后两排抗滑桩所承担的总荷载的百分比例[12].
不同桩间距与前后排桩承担滑坡推力比例关系曲线如图10 所示,在桩间距较小时,后排桩承担滑坡推比例越大,而前排桩承担的滑坡推力比例越小,随着桩间距的增大,后排桩承担滑坡推比例减小,而前排桩承担的滑坡推力比例增大,前后排桩有承担的滑坡推力比例均分的趋势,最终,随着桩间距的增大,后排桩承担滑坡力推比例增大,而前排桩承担的滑坡推力比例减少.

图10 桩间距与前后排桩承担滑坡推力比例关系图
双排式钻孔抗滑桩通过把桩顶的承台前后两排桩连接,提高了承载能力,又通过机械钻孔施工提高了施工的速度.本文研究的双排式钻孔抗滑桩主要采用干式旋挖钻孔灌注桩技术,具有不需要泥浆护壁,成桩质量高,施工速度快、安全性好、节省造价等优点.综合表明,在确定的排间距时,在桩间距小于3d 较小时,由于后排桩对前排桩的遮蔽作用,前排桩的土拱效应不明显,表现为后排桩承担的滑坡推力比例较大,而前排桩承担的滑坡推力比例较小,不利于发挥共同前后排桩的抗滑效果.在桩间距在3d~6d 时,前后排桩的土拱效应明显,表现为前后排桩承担的滑坡推力比例差距较小,有利于充分发挥前后排桩的抗滑效果.在桩间距在大于6d 时,前后排桩的土拱效应不明显[9,14],表现为前后排桩承担的滑坡推力比例差距明显,不利于发挥共同前后排桩的抗滑效果;一般认为抗滑桩治理边坡后,结构的桩前水平位移越小,则认为治理效果越好[12],所起取双排式钻孔抗滑桩结构的桩顶整体水平位移作为衡量其治理滑坡效果的主要标准之一,所以认为桩间距不宜大于6d.
3 结语
(1)随桩间距的增大,双排式钻孔抗滑桩前后排桩的桩顶最大位移增大,前后排桩桩身弯矩和剪力最大值位置基本不变,前后排桩桩身弯矩和剪力的分布变化很小,而对桩身最大弯矩值和最大剪力值影响明显,直到桩间距过大不能形成有效的土拱效应滑坡土体从桩间挤出,双排抗滑桩失效.
(2)在桩间距较小时,前后排桩承担滑坡推力比例差距较大;随着桩间距的增大,前后排桩承担滑坡推比例有均分的趋势,最终,随着桩间距的增大,前后排桩承担滑坡推力比例又相差较大.
(3)桩间距取3d~6d,既能前后排桩的土拱效应越明显,又能使前后排桩承担的滑坡推力比例差距较小,在双排式钻孔抗滑桩的设计中,建议取3d~6d桩间距作为参考范围.
(4)本数值模拟中作了假设和简化,实际工程中排间距、滑体特性等也是影响因素,建议在考虑滑体的特性情况下变化桩间距和排间距进一步研究.
[1]熊治文,马辉,朱海东.全埋式双排抗滑桩的受力分布[J].路基工程,2002(3):5-11.
[2]何颐华,杨斌,金宝森,等.双排护坡桩试验与计算的研究[J].建筑结构学报,1996,17(2):58-66.
[3]杨明辉,汪罗成,赵明华.考虑土拱效应的双排抗滑桩桩侧土压力计算[J].公路交通科技,2011,28(10):12-17,39.
[4]王成华,陈永波,林立相.抗滑桩间土拱力学特性与最大桩间距分析[J].山地学报,2001,19(6):556-559.
[5]王乾坤.抗滑桩的桩间土拱和临界间距的探讨[J].武汉理工大学学报,2005,27(8):64-67.
[6]韩爱民,肖军华,梅国雄.被动桩中土拱效应特征与影响参数研究[J].工程地质学报,2006,14 (1):111-116.
[7]张建勋,陈福全,简洪钰.被动桩中土拱效应问题的数值分析[J].岩土力学,2004,25 (2):174-178.
[8]周德培,肖世国,夏雄.边坡工程中抗滑桩合理桩间距的探讨[J].岩土工程学报,2004,26 (1):132-135.
[9]毛晓光.双排式-小直径钻孔抗滑桩桩土相互作用机理研究与应用[D].重庆:重庆交通大学,2011:30-38.
[10]黄小艳,徐年丰,王汉辉,等.双排抗滑桩受力规律的数值研究[J].人民长江,2012,43(2):4-8.
[11]沈新普,王琛元,周 琳.一个钢筋混凝土损伤塑性本构模型及工程应用[J].工程力学,2007,24(9):122-128.
[12]欧孝夺,唐迎春,崔伟,等.h 型抗滑桩模型试验及数值模拟[J].岩石力学与工程学报,2012,31(9):1936-1943.
[13]刘金龙,王吉利,袁凡凡.不同布置方式对双排抗滑桩土拱效应的影响[J].中国科学院研究生院学报,2010,27(3):364-369.
[14]吕庆.边坡工程灾害防治技术研究[D].杭州:浙江大学,2006:93-116.

