供水管网水力模型与优化调度模型的建立与展望

刘济嘉

（沈阳建筑大学，市政与环境工程学院，辽宁 沈阳 100168）

0 引言

上世纪六十年代，国外就把计算机技术应用于供水系统的管理与调度中，近年来，随着我国经济的蓬勃发展和人们生活水平的提高，国家城乡建设部最近颁布的相关的文件中明确提出，人们对水的需求增大对供水企业提出了更高的要求，提高供水水质和供水安全可靠性，降低供水能耗、管网漏损和药耗是供水企业目前亟需解决的问题。要解决这些问题的前提与基础是实时的掌握输水系统的水量，水压，水头损失，漏失量等其他细节运行情况，这些信息通过遥感设备变为数字信息传递到中心控制室，通过这些返回的技术参数研究人员就可以对供水系统运行状态进行判断并作出相应的决策。

城市供水系统的优化调度主要分为预测，管网水力模型和优化调度，工作人员可以通过他们远程监控系统运行情况。根据预测周期的长短，城市用水量预测的范围很宽，大到城市年用水量预测、小到城市时用水量预测都可以进行预测；通过微观水力模型和宏观水力模型可以建立供水系统水力计算模型；优化调度模型可以根据水力模型的显示结果自动制定决策。

1 城市水量预测模型

通过对某一时段的用水量历史数据资料建立模型来估计后一时段的用水量的方法叫城市用水量预测。供水系统预测模型可以预测水量的时间跨度很大，根据预测时间跨度可以分成短期预测和长期预测。短期预测主要依据最新的实际用水量数据来预测未来几天的水量，作用是对未来几天管网中水的调度提前预计并制定决策措施，以免水量突发引起的管网故障。长期预测的结果主要为城市规划，水厂规划以及管网的建设等提供依据，它是根据目前某城市的人均生产总值和人口的增长速度等基本参数进行的粗略预测。

1.1 逻辑性预测法

在用水量预测过程中，逻辑性预测法(原因预测法)是通过假定系统中输出变量和输入变量之间存在逻辑的因果关系，通常考虑温度、气候、湿度之间的内在关系以及与城市用水量的关系构建出的函数关系式，有逻辑依据，可以普遍让人接受且预测方法准确。但是，该类模型需要大量的基础资料，预报较为复杂，从而限制了广泛运用。

1.2 时间数据分析法

通过分析时间上相邻有序数据并运用统计学知识建立数学模型预测城市水量的方法叫时间数据分析法。该方法在预测过程中认为序列中的结果只与时间有关，而不考虑其他因素的影响也就是只考虑观测值和预测结果之间的变化关系，历史数据资料的模式完全决定预测的整个模型，因此时间序列预测方法更快捷、高效，但实际上水量预测与众多因素有关所以该方法缺乏理论性，不能在理论上判别预测值的正确性及误差范围等。常用的时间序列分析方法如下：

（1）移动算数平均预测法

在统计学中，算数平均数是较好的序列估计量，但其缺点是无法反应数据的变化情形，移动算数平均法能较好的解决普通算数平均预测方法的不足。该方法的优点是计算简单水量预测的数据较保守，缺点是需要大量历史基础资料，且预测数据的变化规律照比实际变化趋势有滞后性，水量变化大的城市的水量预测，只适用于水量变化较平稳的城市的水量预测。

（2）单指数平滑法

单指数平滑法计算方便且需要的基础资料较少，因而得到广泛的应用，但该方法水量预测的结果并不十分准确。相比移动算数平均法需要大量数据，单指数平滑法只需要获得当前时段及上一时段的观测数据X、Yt及平滑参数a，单指数平滑模型就能进行一个周期的预测，模型如式（1）所示，其中xt 为时间序列值，a为平滑常数，可以根据经验确定，取值大约在0.01-0.3 之间，当a 取值较小时，用水量随时间变化较为缓慢，预测结果较为平滑，当a 较大时，用水量预测值随时间变化较为敏感。

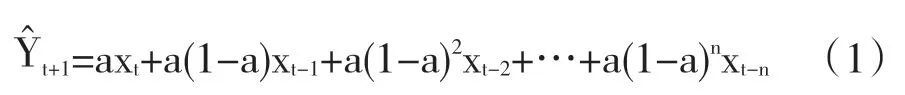
（3）回归预测法

建立回归模型所需要的条件是一个时间序列y1，y2，y3，y4…yt的历史数据资料平均数u，水量预测回归模型的模型公式如图（2）所示，其中et为测量数据与实际数据之间的估计误差；Φ1、Φ2、…、Φp为水量预测模型回归系数；p为水量阶数；yt-1、yt-2、…、yt-p分别为历史p个时段的观测资料。

（4）自回归移动平均预测模型

建立P阶自回归移动平均混合模型时需要把自回归、移动平均模型都包括在内，模型方程式如式（3）所示，其中φ1、φ2、…、φp，θ1、θ2、…、θp为模型系数。。

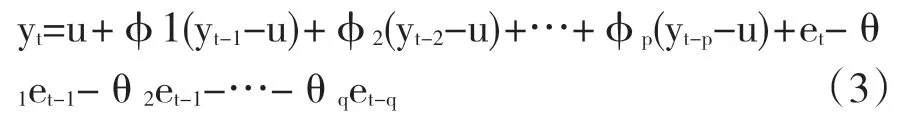
（5）BP神经网络预测法

城市短期用水量预测的输入与输出的对应关系不属于线性类型，有学者认为他们之间的关系是“非线性多变量离散排布”。影响城市短期用水量预测的输入与输出之间关系的因素十分复杂，BP 神经网络模型能够精确的描述出输入量与输出量之间的复杂因果关系，因此可以建立BP 神经网络解决城市短期用水量预测问题。设计神经网络模型预测城市用水量，首先需要确定输入层，隐含层，输出层的数量及它们的关系，如图（1）所示，利用城市前n 天的用水量X（t）（t=1，2，…，n）对设计好的模型进行驯化，再利用驯化好的神经网络模型预测第（n+1）天的用水量。

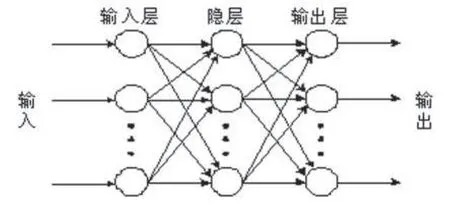
图1 神经网络模型的结构设计方法

2 供水管网水力计算模型的建立

2.1 宏观水力模型

供水管网的流量服从“比例负荷”，该水力管网的建模可以应用宏观水力模型，该模型可以考察给水系统的“输入量”与“输出量”之间的关系。和神经网络一样，它也是基于“黑箱理论”，它忽略系统内部结构且无需求解复杂的高阶非线性方程组，所以该模型的计算速度比一般速度快，反应灵敏，能快速的反应管网宏观模型的运行状态，但计算精度不高。

水厂的送水压力和供水流量等实测数据是管网宏观水力模型的基础，利用统计学的方法建立经验公式，通过经验公式求解表征供水系统状态的几个特征参数，它的优点是计算速度快，所需原始资料少等，但建模的精度不高，且只适用于满足“比例负荷”的供水管网。在实际工程中管网一天内用水量往往不满足比例负荷的要求，在不满足要求时，可将一天分成若干时段，近似认为每个时段内的比例关系固定不变，即该时段内基本上满足“比例负荷”条件，就可以应用宏观模型估计计算。

2.2 管网微观模型及建立基本原理

供水管网微观模型通过建立管网的连续性方程和能量方程组分析供水系统的拓扑结构，获得管网中各种详细的运行参数，比如管段的流量、管内流速、各管段压力水头、节点的局部水头损失、漏失量等。它能直接运用管网资料的全部信息资料库，得到的结果数据详细全面，但该方法计算工作量大，计算时间长，所需原始资料多。在实际工程中由于管线过于复杂复杂且次要管线对整个管网系统的影响不大，通常保留主要管线，省略次要的管线，以化简管路简化运算，但简化时要注意简化后的管网仍然能够反映实际的供水情况。管网微观模型能实时监测管网运行状态，对于供水管网的科学现代化管理有积极的作用。

给水管网计算的实质是联合求解连续性方程、能量方程和降压方程。计算环状管网时，首先需要满足连续性方程，之后对供水系统进行节点流量初步分配，并根据初分配的流量确定管径之后，带入能量方程求出流量校正，根据流量差值对管道的流量进行再分配，反复计算直至管网满足能量方程的要求，此过程叫做管网平差，一般采用Hardy Cross法。

3 水力管网优化调度模型

3.1 水力管网的直接优化调度

水力管网的直接优化调度的决策变量是水泵的运行方案，直接优化调度适用于泵站规模较小，水泵种类及数量较少，缺少调速泵的情况下，水泵运行方案的改变主要指水泵的开启状态和水泵转速。

3.2 水力管网的两级优化调度

水力管网的两级优化调度的决策变量是送水泵房的出口流量，首先确定调度周期内泵房的流量分配，在流量分配基础上二级寻优，获得水泵的运行方案。两级优化调度适用于供水规模大，水泵运行组合数多，泵站内安装有调速泵，可调余地大的供水系统。

4 城市水利模型的发展展望

（1）城市的用水量由国民平均生产总值、城市人口数量、人民生活水平、工业发展水平等多个因素共同影响。当前研究的重点是考虑城市水量预测与上述因素之间的关系，再结合城市用水的影响因子建立科学准确的预测方法。

（2）建立延时动态的多工况水力模型，基于微观水力模型的在线优化调度，提高模型软件在不同城市的通用性是未来研究的重点。

［1］袁一星.城市给水管网工况模拟技术及其应用的研究：［北京工业大学博士学位论文］.北京：北京工业大学环境科学与工程学院，2005，70-75.

［2］欧阳嘉.给水管网水力建模与优化调度应用研究：［湖南大学硕士学位论文］.湖南：湖南大学土木工程学院市政工程，2012，20-35.

［3］许强，盛宁，等，城市给水系统优化调度研究综述［J］.南水北调与水利科技，2008，6（3）：115-117.

［4］安明阳，付晚霞，韩伟，等.城市供水三种时用水量预测的研究［J］给水排水，2012（38）：229-231.

［5］张薇，邹志红，王慧文，等.城市日用水量模型及其应用［J］系统工程2010，28（3）：93-97.

［6］徐瑾，赵涛，等.城市生活需水量预测中智能算法的应用研究［J］中国给水排水，2012，8（21）：66-68.