复数多维标度移动定位算法
张瑀琪 万 群
(电子科技大学电子工程学院,成都610054)
引 言
无线定位技术在现代社会中发挥着日益重要的作用,其广泛应用极大地改变了人们的生活方式,已成为了移动通信及无线传感器网络的重要应用。利用到达时间(Time of arrival,TOA)测量信息,对静止目标进行移动定位一直是个热门的课题。固定传感器的位置,不仅能得到准确的节点位置信息,更能减少用来测量节点间距离的辅助测量设备,使其成为无线定位的研究热点。另一方面,这可以表示为一个典型的多维标度(Multidimensional scaling,MDS)问题。
MDS广泛应用于心理学、地质学及分子生物学等领域的数据分析中。近几年来,Cheung和So[1]提出一种用于蜂窝网络中的移动台定位的修正MDS方法,Wan[2]等得到了一个基于3个基站的多维似分析的噪声子空间算法,Wei[3]等提出以定位节点为参考点的加权MDS方法使稳健性在低信噪比下增强。这些MDS算法经过验证表明较之传统算法,对噪声具有更强的稳健性。
针对直达波环境下的无线定位问题,利用MDS技术,分两步进行目标移动站定位。首先生成标度矩阵以表示两两距离间的相似性度量,然后求解一组相关于标度生成矩阵的信号子空间或者噪声子空间线性方程,使用最小二乘[4-5](Least squares,LS)方法估计未知目标移动站位置。事实上,由于标度生成矩阵的构造与奇异值分解的过程,基于MDS线性方程求解的定位方法并不能得到很好的性能。本文提出了一种新的基于TOA[6-7]的复数 MDS目标移动站定位方法。
1 经典MDS回顾
传感器定位的任务在于利用少数已知位置的节点确定网络中其余多数节点的位置。MDS定位方法通过构建距离平方矩阵,转到内积空间中进行求解,是一类与几何方程无关的定位方法,已被广泛应用于无线传感器网络中的节点定位[8-11]。
需要确定的目标移动站坐标位置表示为z0=[x0y0],第i个传感器坐标位置表示为[xiyi],i=1,2,…,M,M为传感器的总数量。根据TOA测量,其值与光速相乘,目标移动站与第i个传感器间的距离表示为

式中:qi代表测距噪声,在此假定qi为一个零均值的随机过程。利用传感器与目标移动站的坐标信息构造一个M×2的矩阵
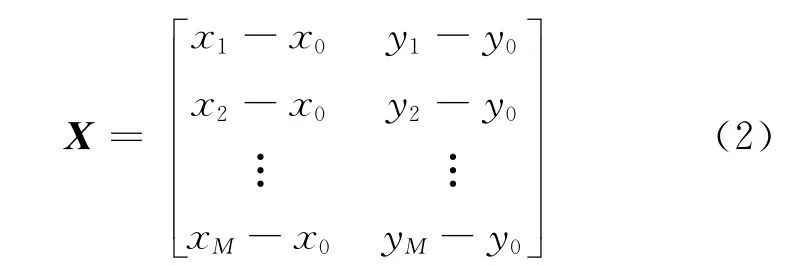
然后定义似然矩阵D=XXT。可知矩阵D的秩为2。D中的(i,j)位值为
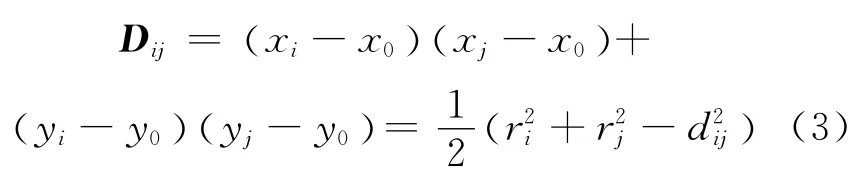
式中:dij为第i个传感器与第j个传感器之间的距离对对称矩阵D进行奇异值分解

式中Λ=diag(λ1,λ2,…,λM)为矩阵D的特征值对角矩 阵,且λ1≥λ2≥ … ≥λM≥0。U=[u1u2…uM]为D的特征值对应的特征向量构成的标准正交矩阵,其中U′=[u3u4…uM]为对应噪声子空间。由于D的秩为2,3=0。展开得到

那么,目标移动站的位置可以表示为
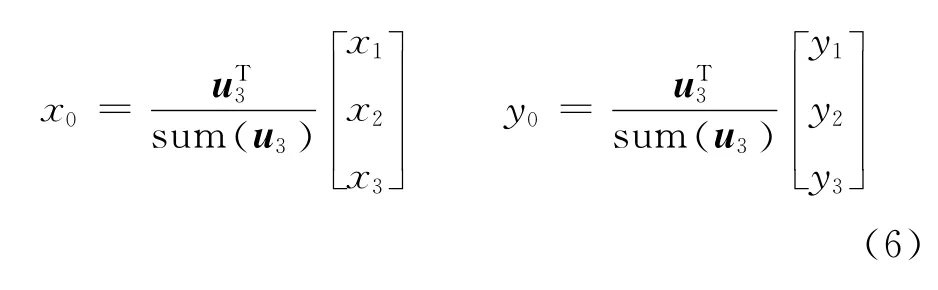
2 复数MDS估计
与经典MDS算法不同,复数MDS算法利用传感器位置坐标信息构造一个M×1的复数矩阵P,结合了MDS算法中二维的数据
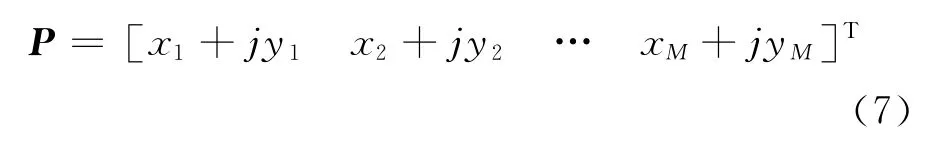
另外,定义P0=x0+jy0为需测量的目标移动站位置。假设第i个传感器与目标移动站的距离为ri,第i个传感器与第j个传感器之间的距离为dij。定义一个对称复数矩阵D
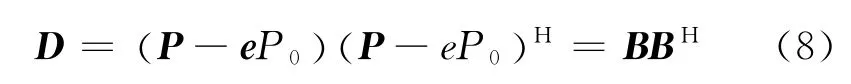
式中:e为M×1的全1列向量,B=P-eP0。可知矩阵D的秩为1。D中的(i,j) 位值均为复数

式中:θi与θj为Pi-eP0与Pj-eP0的向量角。易知
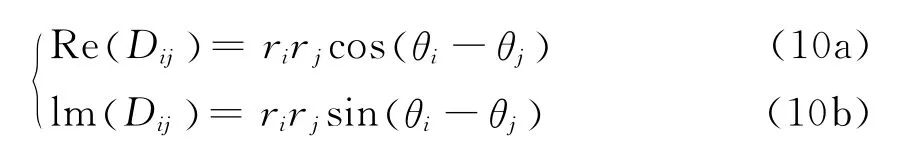
两个向量角的差值用θij表示,可得到
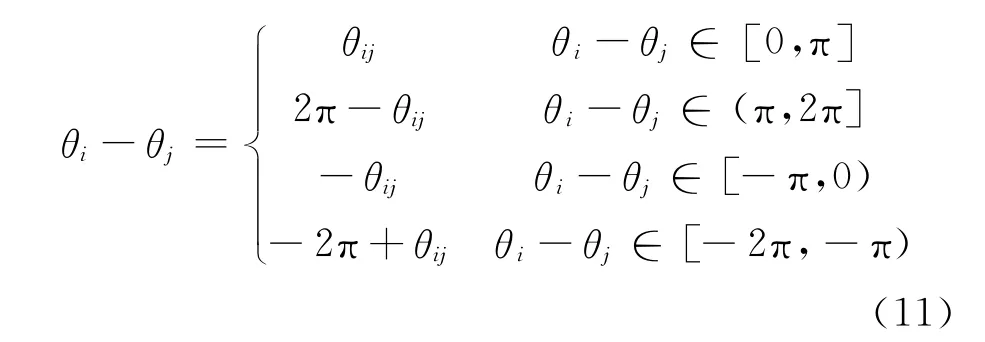
式中:θij为矢量Pi-eP0与矢量Pj-eP0的夹角。
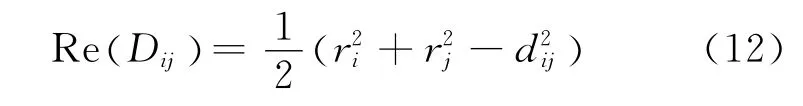
由于
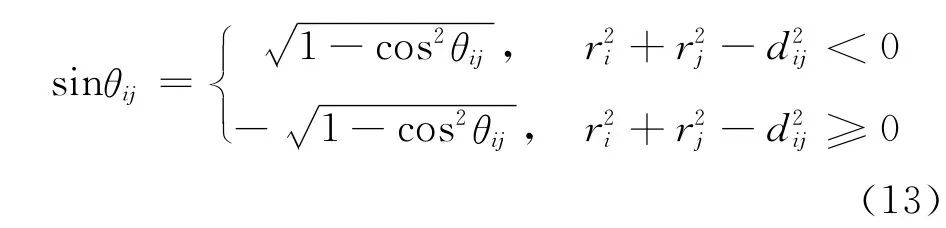
对复数对称矩阵D进行奇异值分解

式中Λ=diag(λ1,λ2,…,λM)为矩阵D特征值构成的对角矩阵,且λ1≥λ2≥…≥λM≥0。列为特征值对应的标准正交矩阵U= [u1u2…uM]。B的最小二乘估计为

式中:Ω为未知的坐标旋转矩阵
D的秩为1,由式(15)可得其中α为一复数。
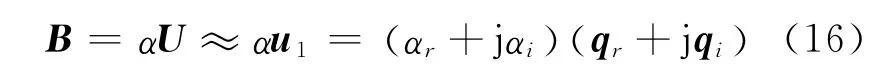
于是可以列出这样一个等式
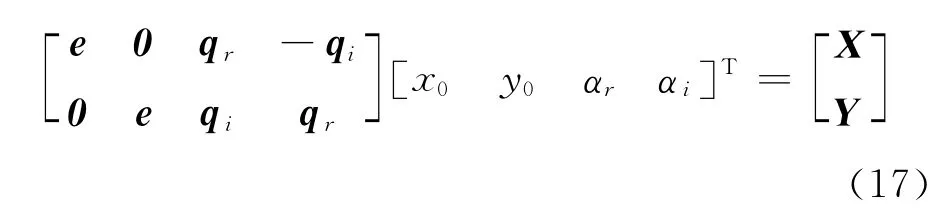
本文提出利用最小二乘复数MDS的定位方法,由下式给出目标移动站的位置估计
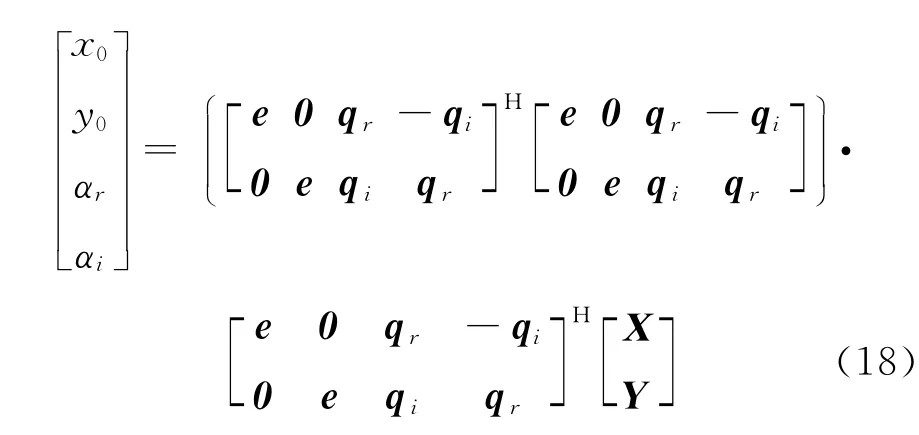
将复数数据矩阵引入到MDS方法中,基于移动站与基站两两距离构成的对称复数矩阵D的最小二乘估计,增加了二维数据之间的相关性(例如其向量角与差值),尽可能减少丢失的距离信息,从而做到更加精确有效的定位。
3 仿真结果
本文的定位仿真评价定位准确率的度量由定位结果的均方误差(Mean square error,MSE)表示,单位取并与理论上无偏定位估计器的克拉美罗下界比较。计算MSE的方法为其中E[·]表示求统计量的期望,通常用时间平均值来代替。
克拉美罗下界(Cramer-Rao lower bound,CRLB)为无偏线性估计能达到的最小方差,并为比较无偏估计量的性能提供一个标准。从目标移动站的高斯测量矩阵可以得到
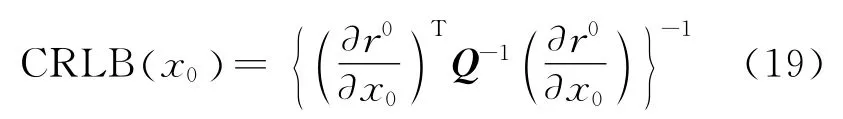
对本文的复数MDS算法与经典的MDS方法、改进MDS以及归一化子空间方法方法进行性能比较,也与克拉美罗下界相比较。首先由3个位置为(0,0)m,(0,5 000)m,(5 000,5 000)m 的传感器对目标移动站进行定位,然后加上同坐标的传感器(5 000,0)m,(5 000,-5 000)m,(-5 000,0)m,(-5 000,-5 000)m,(0,-5 000)m,(-5 000,5 000)m。测量噪声qm为方差=/SNR的零均值高斯过程,SNR为信噪比。所有的结果均为1 000次独立仿真的平均值。
在第1组仿真中,设定目标移动站的位置固定为(-3 000,500)m。图1为当信噪比固定在30dB时目标移动站位置估计值随基站个数变化的均方误差值。可以看出,几种MDS方法的性能随着定位参考点个数的增多而提高。其中,改进MDS与归一化子空间方法均方误差相差不大,而复数MDS性能较之更好。当基站数量为4站时,MDS算法与克拉美罗下界相差高达5dBm2,而复数MDS算法与克拉美罗下界相差只有2dBm2。
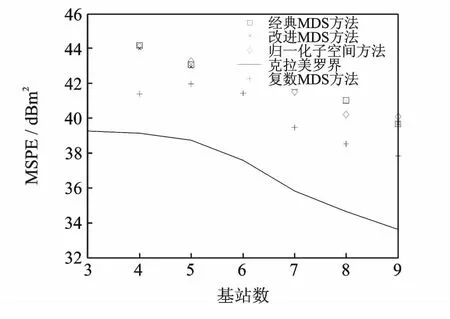
图1 当Z0=[-3 000 500]m时随基站数量变化的均方误差Fig.1 MSPE versus number of BSs when Z0=[-3 000 500]m
图2为基站个数固定为四站时,均方误差与信噪比之间的关系。从图中可以看出,几种MDS方法的性能随着信噪比的增加而提高,在较低信噪比情况下很不稳定。在信噪比的增加过程中,复数MDS方法显示了更好的性能及更强的稳健性。特别是在信噪比为7时,改进MDS与归一化子空间方法的均方误差与克拉美罗下界相差大约为21dBm2,而复数MDS方法则相差不到0.5dBm2。

图2 当Z0=[-3 000 500]m时随信噪比变化的均方误差Fig.2 MSPE versus SNR when Z0=[-3 000 500]m
4 结束语
本文提出了一种针对移动定位的新颖的复数多维标度估计算法,与现有对标度生成矩阵进行奇异值分解的MDS算法不同,本文的方法依靠于构造的复数矩阵从而利用了更多的信息量。本文算法比经典的MDS算法性能有明显的提高,并且在中等噪声情况下性能接近于定位估计的克拉美罗下界。
[1]Cheung K W,So H C.A multidimensional scaling framework for mobile location using time-of-arrival measurements[J].IEEE Trans Signal Process,2005,53(4):460-470.
[2]Wan Q,Luo Y J,Xu J,et al,Mobile localization method based on multidimensional scaling similarity analysis[C]∥Proc Int Conf Acoustics,Speech,Signal Processing(ICASSP).Philadelphia:PA,2005:1081-1084.
[3]Wei H W,Wan Q,et al.A novel weighted multidimensional scaling analysis for time-of-arrival-based mobile location[J].IEEE Transactions on Signal Processing,2008,56(7):3018-3022.
[4]Beck A,Stoica P,Li J.Exact and approximate solutions of source localization problems[J].IEEE Transactions on Signal Processing,2008,56(5):1770-1778.
[5]Cheung K W,So H C,Ma W K,et al.Aconstrained least squares approach to mobile positioning[J].EURASIP Journal on Applied Signal Processing,2006(2006):1-23.
[6]Caffery J J.A new approach to the geometry of TOA location[C]∥Proc IEEE Vehicular Technology Conf.[S.l.]:IEEE,2000:1943-1949.
[7]Riba J,Urruela A.A robust multipath mitigation technique for time-of-arrival estimation[C]∥Proc IEEE Veh Technol Conf.[S.l.]:IEEE,2002:2263-2267.
[8]Yang Z.A survey on localization in wireless sensor networks[D].Hong Kong:The Hong Kong University of Science & Technology,2008.
[9]So H C,Chan K W.A generalized subspace approach for mobile positioning with time-of-arrival measurements[J].IEEE Trans Signal Process,2007,55(60):5103-5107.
[10]Spirito M A.On the accuracy of cellular mobile station location estimation[J].IEEE Trans Veh Technol,2001(50):674-685.
[11]Fenwick A J.Algorithms for position fixing using pulse arrival times[J].Radar,Sonar and Navigations,1999,146(4):208-212.

