基于接收信号强度的非视距检测与修正算法

赵泰洋 郭成安

（大连理工大学电子信息与电气工程学部，大连，116024）

引 言

在基于到达时间（Time of arrival，TOA）的定位系统中，当移动节点与定位基站间存在障碍物时，无线信号只能以非视距（Non－light of sight，NLOS）方式传播。在这种情况下基站得到的TOA值就会存在NLOS误差。NLOS误差已成为影响无线定位系统定位性能的一项重要因素。随着移动节点所处环境的变化，NLOS误差呈现不同的分布［1］，因此如何减少其对定位性能的影响已成为当前的一个研究热点。现有的NLOS误差处理算法，大多分成两个步骤：（1）对TOA测量结果进行检测，判断其中是否含有NLOS误差；（2）采用一定的方法对含有NLOS误差的TOA值进行修正，减小NLOS误差的影响。

对于TOA值中NLOS的检测，常用的方法可分为两类：（1）对一系列TOA值进行分析的方法，如文献［2－4］中，分析采集到的多个TOA值的概率分布函数，文献［5］采用对多个TOA值进行平滑处理的方法检测NLOS误差。文献［2－5］的方法都需要短时间内多次测量TOA值，这样会大大增加移动节点的功耗，这与移动节点的小体积、低功耗的要求是矛盾的。文献［6－7］提出了一种迭代残差法，该方法适用于提供TOA值的基站数量大于最少基站数的情况，当参与定位的基站数量较少时体现不出其优势。文献［8，9］针对超宽带（Ultra wide bandwidth，UWB）系统提出了一种基于多径分量统计特性的NLOS检测方法，但该方法不适用于传统的调制通信系统。

另一类就是采用TOA与其他信号参量（如波达方向，信号强度）进行数据融合的方法［10－12］。因为采用了另一个维度的信息，有可能得到更好的结果。但这类方法其计算量通常也要大于第1种方法。对于含有NLOS误差的TOA值，文献［5－7］直接放弃含有NLOS误差的TOA值，这种方法适用于有多个可选TOA值的情况，但当移动节点附近基站较少时，无法采用这种方法。在这种情况下常采用 Kalman滤波［2－4］或加权最小二乘法［8］抑制NLOS误差。

本文提出一种采用（Receive signal strength，RSS）与TOA数据融合的方法，通过检测RSS的变化程度来修正TOA测量值。该方法首先利用TOA测量值与RSS值之间的关系，得出该TOA测量值中存在NLOS误差的可能性。之后根据该可能性的大小对TOA测量值进行修正，最后用修正后的TOA值进行定位。实际应用结果表明，本文提出的算法与单纯基于TOA的定位方法相比，可有效地抑制NLOS对TOA值的影响，从而提高定位精度。

1 系统模型

本文讨论的基于TOA的无线定位系统中，基站与移动节点通信，在通信过程中获取移动节点到基站的TOA和基站接收信号的RSS。在LOS信道环境下的TOA测量值为

对于NLOS信道环境

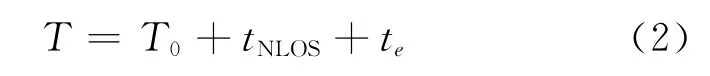
式中：T0为移动节点和基站间电波的视距传播时间，te为由TOA测量系统引起的均值为零的高斯随机变量。tNLOS为由NLOS所引起的附加时延，是一个均值大于零的随机变量。

对于RSS，参照文献［13］中的公式，可得到LOS信道的RSS值表示为

NLOS信道的RSS值表示为

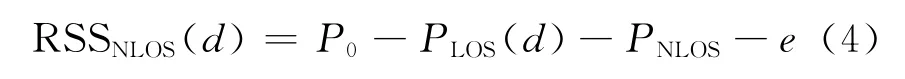
式中：P0为移动节点的发射功率；PLOS（d）为信号在空气中的传播损耗，是一个与传播距离有关的量；e为测量误差，是一个均值为零的高斯随机变量；PNLOS为在NLOS传播过程中信号在反射点的反射损耗，是一个均值为正的随机变量。

2 算法描述

2.1 NLOS误差检测

在本文讨论的定位系统中，假设移动节点与某一基站间距离为d0，在视距（Light of sight，LOS）传播时，对应的TOA值为T0。对于NLOS传播的情况，当信号经过反射后，信号的传播路程为d，对应TOA值为T。显然d大于d0，T大于T0。此时测得的信号强度为RSSNLOS。根据式（3）可以计算出LOS传播情况下距离为d时，基站接收信号强度为RSSLOS。定义这两种情况下的接收信号强度的变化量为ΔRSS，即

从式（3，4）可知，理论上这个差值ΔRSS即是反射损耗PNLOS，为一个非负的值。在实际应用中，由于测量误差的存在，该差值有可能为一个绝对值较小的负数。

ΔRSS可以反应信号的传播状态，ΔRSS越大，说明信号在传播过程中附加损耗越大，即存在NLOS传播的可能性就越大。由于无线传播环境的复杂性，很难给出一个阈值来准确判断一个TOA测量值中是否含有NLOS误差，因此采用软判决的方法，定义一个反映存在NLOS可能性的参数RNLOS如下

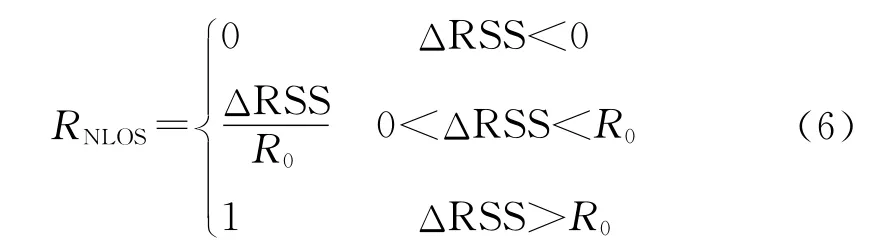
式中：R0为一个归一化因子，其值与系统的具体工作环境有关。

2.2 采用RSSI值对含有NLOS误差的TOA值进行修正

对于2.1节讨论的NLOS测距，若能找到ΔRSS与tNLOS之间的关系，即可在一定程度上消除NLOS对TOA测量值的影响。但由于移动节点的位置及周围环境有极大的不确定性，不可能找到一个确定的函数关系从ΔRSS精确解出tNLOS。然而通过对大量实验数据的分析，发现NLOS误差与ΔRSS之间有一定的统计关系。例如，NLOS误差的均值与ΔRSS有一定的相关性。利用这一相关性，设法得到二者之间的统计关系，从而可以对TOA测量值进行修正，以降低NLOS误差对TOA测量结果的影响。

根据这一思路，本文设计一个具体实现的算法。该算法分为统计学习和误差修正两个步骤。

在统计学习步骤中，设法得到定位系统中无线信号的传播特性，该步骤的具体算法如下：

（1）确定出无线信号在LOS传播情况下的信号强度与传播距离之间的关系，即式（3）的具体表达式。

（2）对于不同的ΔRSS，通过测试实验，计算出tNLOS的均值MNLOS，用于后续对TOA测量值的修正。MNLOS可表示为

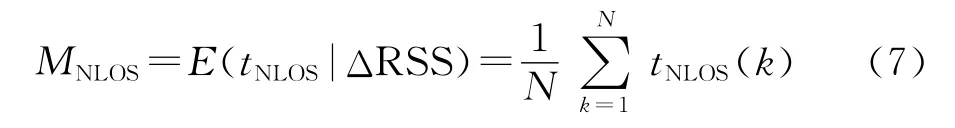
式中：N为测试次数。

在误差修正步骤中，当基站测量得到一组TOA值和RSS值后，采用下面的算法对TOA值进行修正：

（1）利用式（3）计算出LOS情况下对应TOA测量值的RSS值RSSLOS。

（2）按式（5）计算 RSSLOS和RSS测量值的差值ΔRSS。

（3）利用该组ΔRSS和式（7）计算出均值MNLOS。

（4）对TOA测量值进行修正：从TOA测量值中减去MNLOS，得到修正后的TOA值。

3 算法实现

为了考查本文提出的算法性能，本文设计了一个基于NanoPAN扩频测距模块的室内无线定位实验系统。NanoPan测距模块是由Nanotron公司生产的一款工作于2.45GHz频段的射频通信模块，采用Chirp扩频调制，通信带宽最大为80MHz。该模块采用对称双边双路测距方式。该方式利用测量数据包在两个模块间进行双向传输的时间来计算TOA。这种方式不需要两个节点的时钟同步，降低了对硬件时钟的要求。除TOA外，该模块还提供接收机中可变增益放大器（Variable gain amplifier，VGA）的放大倍数。该VGA采用自动增益控制（Automatic gain control，AGC），使输出信号强度P基本保持不变，所以可以从AGC值（即VGA的放大倍数）计算出接收信号强度RSS来，即

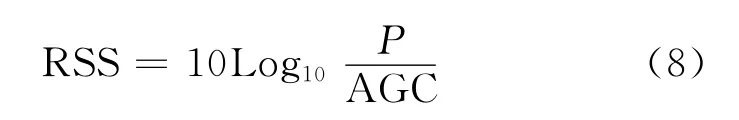
该实验系统采用基于基站的定位方式。基站与移动节点均采用NanoPan作为射频通信模块。移动节点在与基站通信的过程中，基站可得到移动节点到基站的TOA和此时基站接收机中的AGC值。然后基站将这两个信息通过网络传输给数据处理中心，计算出修正后的TOA值。采用同样的方法，利用多个基站提供的TOA值，然后采用多维标度法（Multidimentional scale，MDS）［14］对移动节点进行定位。

该实验安排在一个长11.8m，宽8.9m的房间中进行。房间一面是玻璃窗，3面是混凝土的墙壁。房间内部有大量高约1.2m的木制障碍物（工作台），这些障碍物对于中间的测试点会造成NLOS问题。该实验场景如图1所示。图1中三角形为基站所在位置，圆圈为移动节点的测试位置。

图1 实验场景分布图Fig.1 Configuration of experiment environment

在实际应用问题中，第1节中给出的TOA测量模型（即式（3，4））所涉及的函数关系及其参数都是未知，因此并不能直接用来计算RSS与TOA之间的关系。针对该问题，本文通过2.2节给出的统计学习算法步骤，以实测方式来近似得到RSS与TOA的关系，进而利用式（7）计算出tNLOS的均值参数MNLOS。

对于该统计算法的具体实施，考虑到Nano－Pan通信模块提供的是TOA值和AGC值，为了减小计算量，本实验直接采用AGC值进行判断。在此情况下，式（3）可修正为

式中：Gd为距离为d时基站接收机中放大器的放大倍数。这时根据式（7），式（5）则修正为

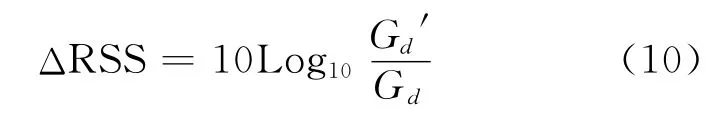
式中：Gd′为实际的AGC测量值。

为了得到式（9）所描述AGC值与距离之间关系的解析表达式，本文设计了如下实验测试步骤：在无遮挡的环境下，测量出移动节点处于不同位置时基站得到的TOA和AGC值。在该实验中，每个位置做50次测量。然后对50次测量结果取α均值［15］，即将50次实验结果按由小到大的顺序排列，之后取中间的30个值的均值作为实验测试值。图2所示的结果（图中的黑点）即为实验所得到的AGC值的α均值。

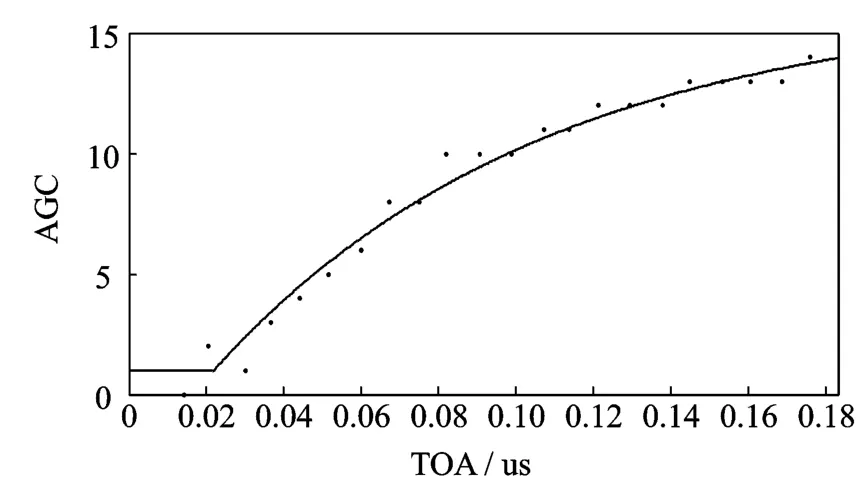
图2 直达波的TOA值与AGC值之间的关系Fig.2 Relationship between TOA ＆ AGC of LOS signal

在得到实测数据后，本文进一步采用指数函数对实验数据进行拟合，以此来得到TOA值t与AGC值Gd之间的解析表达式。在本文的实验中，最后的拟合结果如式（11）所示

图2中的连续曲线即为该拟合函数所给出的曲线。

在得到LOS情况下TOA值与AGC值的关系之后，下一项工作是获得ΔRSS与tNLOS之间的统计关系，即式（7）的统计表达式。根据图1所示的实验环境，取单数号的节点位置作为测试采样点，每个点进行30次实验，记录基站得到的TOA值和AGC值。图3给出了室内测量得到的ΔRSS与测距误差tNLOS的实验结果，在本实验中对该组实验数据进一步采用多项式拟合的方法得到了ΔRSS与测量误差均值MNLOS间的近似解析表达式MNLOS（ΔRSS）＝－0.0041ΔRSS4＋0.086ΔRSS3－

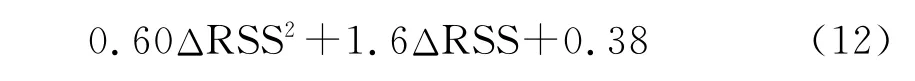
图3中的各个圆圈为各次实验的实测结果，连续曲线则是通过多项式拟合方法获得的解析表达曲线。

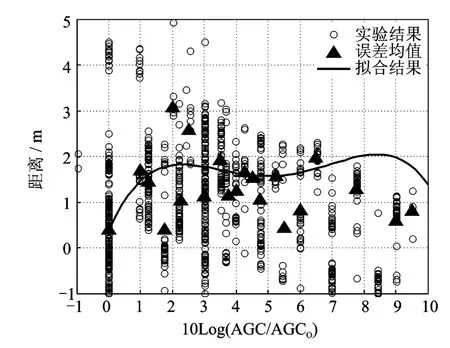
图3 ΔRSS与测距误差的关系Fig.3 Relationship betweenΔRSS ＆ranging error

4 实验结果

4.1 TOA修正实验

该实验仍然在如图1所示的实验环境中进行。实验中采用一个移动节点在不同位置与某一基站通信，得到移动节点到达该基站信号的TOA值和AGC值。然后采用本文在2.2节中给出的误差修正算法对TOA值进行修正。

在此次实验中，移动站分别在如图1所示的位置2，3，11，13，15，18及21号7个位置与基站2进行通信，每个位置通信30次。图中每个位置的数据是30次实验的平均结果。表1是未采用本文修正方法的测量结果，表2是采用了本文修正方法的最终结果。对比表1与表2，可见后者的测量误差较前者有明显的改善。

表1 未采用本文修正方法的TOA测量结果 nsTable 1 Results of TOA measurement without correction

表2 采用本文修正方法的TOA测量结果 nsTable 2 Result of TOA measurement with correction

4.2 定位实验

本文还进行了定位实验。图4给出了移动节点分别在2号，15号和21号位置处各30次未采用及采用RSS的定位实验结果。

图4 两种定位算法的室内定位结果Fig.4 Results of positioning method with and without RSS compensation

表3给出了各个位置上的具体实验结果。表中的数据为平均定位误差，即30次实验的定位结果与真实位置距离之差的平均值。从表3中可见，除了位置11外，对其他各个位置，本文提出的采用RSS补偿的TOA定位方法的定位精度都比直接采用TOA值定位的结果要好。对于位置11，采用本文算法的定位结果略微逊于直接定位算法。因为在11号位置处，虽然与基站之间存在障碍物，但无线信号并没有产生反射，而是穿过了障碍物。这样造成了TOA测量值误差不大的情况下，RSS值却有了较大的衰减。所以在进行TOA误差修正时，跟据RSS的衰减对TOA值进行了较大的修正，使修正结果的误差大于实测值的误差，这样就造成了该处修正效果不佳，但这时二者定位误差均比较小，本文算法并未造成明显的不利影响，而从总体的实验结果来看，这种补偿算法还是比较有效的。

表3 两种定位方法的平均定位误差比较Table 3 Mean positioning error of two positioning methods

5 结束语

本文针对无线定位系统中的NLOS问题，提出了一种采用RSS对TOA值进行补偿的算法，该算法计算复杂度较低，在不增加通信次数的前提下，可提高定位精度。文中采用实验方式在室内环境下实现了该算法，给出了一套具体的算法实施方案，并进行了大量定位实验，实验结果表明该算法是有效的。

［1］Wang Wei，Jost T，Fiebig U C.Characteristics of the NLOS bias for an outdoor－to－indoor scenario at 2.45 GHz and 5.2GHz［J］.IEEE Antennas and Wireless Propagation Letters，2011，10：1127－1130.

［2］黄耀光，高 博，李建新，等.基于平方根UKF双向滤波的单站无源定位算法［J］.数据采集与处理，2013，28（2）：1－7.Huang Yaoguang，Gao Bo，Li Jianxin，et al.Square－Root UKF with forward－backward filtering for single－observer passive location［J］.Journal of Data Acquisition and Processing，2013，28（2）：1－7.

［3］Guan Weiguo，Deng Zhongliang，Yu Yanpei，et al.A NLOS mitigation method for CDMA2000mobile location system［C］∥2nd IEEE International Conference on Network Infrastructure and Digital Content.Beijing，China：IEEE，2010：668－672.

［4］耿剑，张玲华.一种基于修正卡尔曼滤波的蜂窝定位算法［J］.数据采集与处理，2013，28（2）：1－7.Geng Jian，Zhang Linghua，A cellular location method based on modified kalman filter［J］.Journal of Data Acquisition and Processing，2013，28（2）：1－7.

［5］Riba J，Urruela A， A non－line－of－sight mitigation technique based on ML－detection［C］∥ICASSP′04.Montreal，Quebec，Canada：IEEE，2004，2：153－156.

［6］Chen Pi chun.A non－line－of－sight error mitigation algorithm in location estimation［C］∥ WCNC 1999 IEEE.［S.l.］：IEEE，1999：316－320.

［7］Fukuda K，Okamoto E.Performance improvement of TOA localization using IMR－based NLOS detection in sensor networks［C］∥ICOIN 2012.Bangkok，Thailand：［s.n.］，2012：13－18.

［8］Ismail G，Chong Chia－Chin，Watanabe F.NLOS identification and mitigation for UWB localization systems［C］∥ WCNC 2007.Hong Kong，China：［s.n.］，2007：1573－1578.

［9］Guvenc I，Chong C C，Watanabe F，et al.NLOS identification and weighted least squares localization for UWB systems using multipath channel statistics［J］.Advances in Signal Processing，2008，1：1－14.

［10］Wang Z，Zekavat S，Omni－Directed mobile NLOS identification and localization via multiple cooperative nodes［J］.IEEE Transactions on Mobile Computing，2011，11（12）：1－25.

［11］毛永毅，李明远，张宝军.一种 NLOS环境下的TOA／AOA定位算法 ［J］.电子与信息学报，2009，31（1）：37－40.Mao Yongyi，Li Mingyuan，Zhang Baojun.A TOA／AOA location algorithm in NLOS environment［J］.Journal of Electronics ＆ Information Technology，2009，31（1）：37－40.

［12］Wann ChinDer，Chin HaoChun.Hybrid TOA／RSSI wireless location with unconstrained nonlinear optimization for indoor UWB channels［C］∥WCNC 2007.Hongkong，China：［s.n.］，2007：3940 －3945.

［13］Wang Qinghua，Balasingham I，Zhang Miaomiao，et al.Improving RSS－Based ranging in LOS－NLOS scenario using GMMs［J］.IEEE Communications Letters，2011，15（10）：1065－1067.

［14］陈璋鑫.LOS／NLOS无线定位方法研究［D］.成都：电子科技大学，2009.Chen Zhangxin.Research on wireless localization in LOS／NLOS environments［D］.Chengdu：University of Electronic Science and Technology of China，2009.

［15］Bednar J B，Watt T L.Alpha－trimmed means and their relationship to median filters ［J］.IEEE Transacations on Acoustics，Speech，and Signal Processing，1984，32（2）：145－153.