基于种群多样性评价的自适应遗传算法

路 景

（威海职业学院信息工程系，山东威海，264210）

0 引言

成熟前收敛(即早熟现象)就是目前遗传算法中较为突出的问题之一。针对这一问题，本文提出了一种基于种群多样性评价的自适应遗传算法，经实验证明，该方法能够较好地保持种群多样性，并且在提高问题求解的精度等方面也有较好的效果。

1 种群熵

在遗传算法中，常用种群熵来对种群的多样性程度进行度量，种群熵的估算方法主要有以下两种：

第一种方法以种群中个体的适应度分布为依据，根据适应度的集中程度对当前种群多样性进行衡量。第代种群的种群熵的估算方法如下：

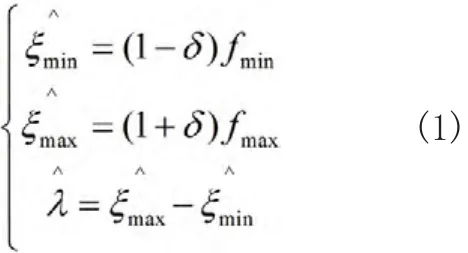
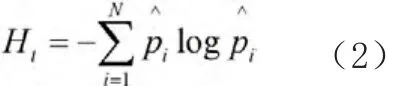
另一种估算种群熵的方法则是以种群中个体编码串的分布情况作为依据，其具体估算方法如下：

1) 假设P(t)为第t代种群，种群规模为N，根据个体编码的不同可将种群划分为个部分，显然，并且对于

4) 计算第t代种群的熵。

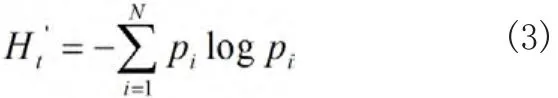
这种种群熵的估算方法反映了种群中不同类型个体的分布情况，但是这种方法有时不能及时反映种群早熟现象的发生，具有一定的滞后性。

针对以上种群熵估算方法各自存在的不足，我们将两种方法进行结合，用第一种估算方法的过于灵敏来弥补第二种估算方法相对滞后的缺点，采用指标作为第代种群的多样性度量，的计算方法如下式：

2 仿真实验

为了评价改进算法的搜索性能，本文在MATLAB 7.0.1环境中分别对标准遗传算法、自适应遗传算法、以及文中改进算法进行实现，并选用2个难度较大的测试函数对以上算法进行了对比仿真实验。

2.1 测试函数及算法

3个测试函数的表达式及具体特征如下：

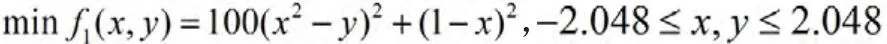
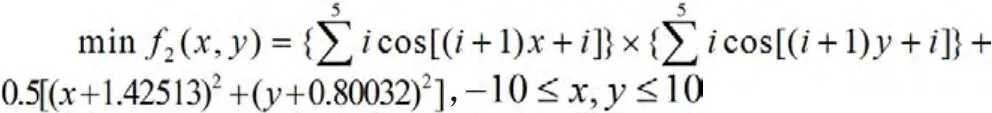
实验中，选用了3种遗传算法与改进算法进行结果比较，以对改进算法的性能进行评价。算法1为标准遗传算法结合最优保留策略；算法2为自适应遗传算法；算法3为无操作概率宏观调整的改进算法，即在文中改进算法基础上，不进行操作概率的宏观调整，其余操作与改进算法相同；算法4为文中改进算法。

2.2 实验结果分析

将每种算法对每个函数均连续运行100次，记录算法停止时的最优解函数值与理想极值的平均误差、寻优成功次数、寻优成功时的平均收敛代数和100次搜索得到的最优函数值，结果如表1、2所示。

表1 四种算法对函数的实验结果

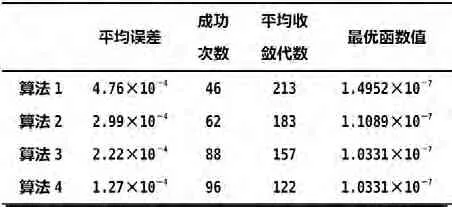
表1 四种算法对函数的实验结果

?

表2 四种算法对函数的实验结果

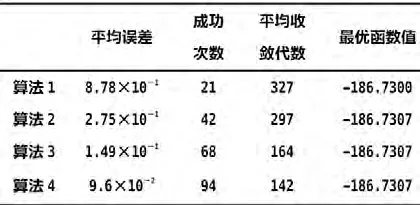
表2 四种算法对函数的实验结果

?

从以上统计数据可以看出改进遗传算法无论是搜索停止时最优解与理想极值的平均误差、寻优成功次数还是寻优成功时的平均收敛代数都比算法1、2、3有一定程度上的提高。根据种群操作概率的宏观、微观调整能够根据当前种群多样性指标及时的提高或降低种群的操作概率，在避免由于种群多样性丧失使算法陷入局部最优的同时保证了算法的收敛速度。改进算法在收敛速度及寻优精度上均优于简单遗传算法及自适应遗传算法。

3 总结

本文以种群多样性评价为基础对遗传算法操作概率的确定方法进行了改进，从宏观和微观两方面对其进行调整，并将小生境技术中的确定性拥挤策略引入新旧个体的替换中来。通过对3个复杂测试函数进行的仿真对比实验表明，改进算法能更好的根据种群当前状态对交叉、变异操作进行控制，避免由于种群多样性丧失造成过早收敛现象的发生。与传统遗传算法相比，改进算法能够较好的保持种群多样性，提升遗传算法的全局寻优能力，提高问题的求解精度。

[1]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1999.110～113

[2]张文修，梁怡.遗传算法的数学基础[M].西安：西安交通大学出版社，2001.104～106

[3]江瑞，罗予频，胡东成等.一种基于种群熵估计的自适应遗传算法[J].清华大学学报(自然科学版)，2002，42(3)：358～361