开孔处应力集中系数的简化计算

张 丽，孙 铁

（辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001）

为了使设备能够进行正常的操作、测试和检修，在壳体和端盖上往往需要有各种开孔并连接接管。开孔的结果，不但会削弱容器壁的强度，而且在开孔附近会形成应力集中，孔径越大，孔边应力集中越严重，其峰值应力通常达到容器壁中基本应力的数倍[1,2]。开孔附近就形成容器的破坏源。因此，必须正确分析开孔附近的应力集中，确保压力容器的正确设计和安全运行。

在计算壳体与接管连接处的最大应力时，工程上常采用应力集中系数法。应力集中系数Kt描述开孔接管处的力学特性。若未开孔时的名义应力为σ，开孔后按弹性方法计算出的最大应力若为σmax，则应力集中系数为[3,4]：Kt=σmax/σ

1 平板开小圆孔的应力集中

单向拉伸平板上开小圆孔时的应力集中如图 1所示，只要板宽在孔径的5倍以上，孔附近任意点（r,θ）的应力分量为[5]：

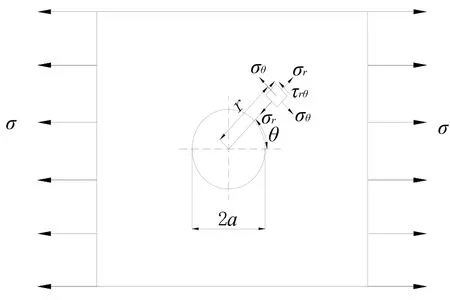
图1 单向拉伸平板上开小圆孔应力示意图Fig.1 Stress about unidirectional tensile plate with a small circular hole diagram

孔边缘r =a处：

在θ=±π/2和θ=0,π的两个截面上，应力分布规律如表1所示。

表1 平板上开小圆孔边缘处应力与基本应力比值的分布规律Table 1 The ratio of edge stress and basic stress about plate with a small circular hole distribution

单向拉伸平板上开小圆孔时的应力集中系数：Kt=3σ/σ=3 。

由此可知，应力随离孔边距离的增加而减小。平板开孔的最大应力总是孔边处的周向应力，并且垂直于拉伸方向的截面上产生3倍的拉应力，平行于拉伸方向的截面上产生1倍的压应力。此方法可用于单向及双向拉伸的平板及壳体上开小圆孔的应力集中系数的计算。

2 应 用

2.1 薄壁圆柱壳开小圆孔的应力集中

中面半径为R，厚度为t的薄壁圆柱壳受内压p作用时，产生两向薄膜应力，分别为周向应力σθ=pR/t和经向应力 σφ=pR/2t[6]，则 σθ=2σφ=σ。如图 2所示。

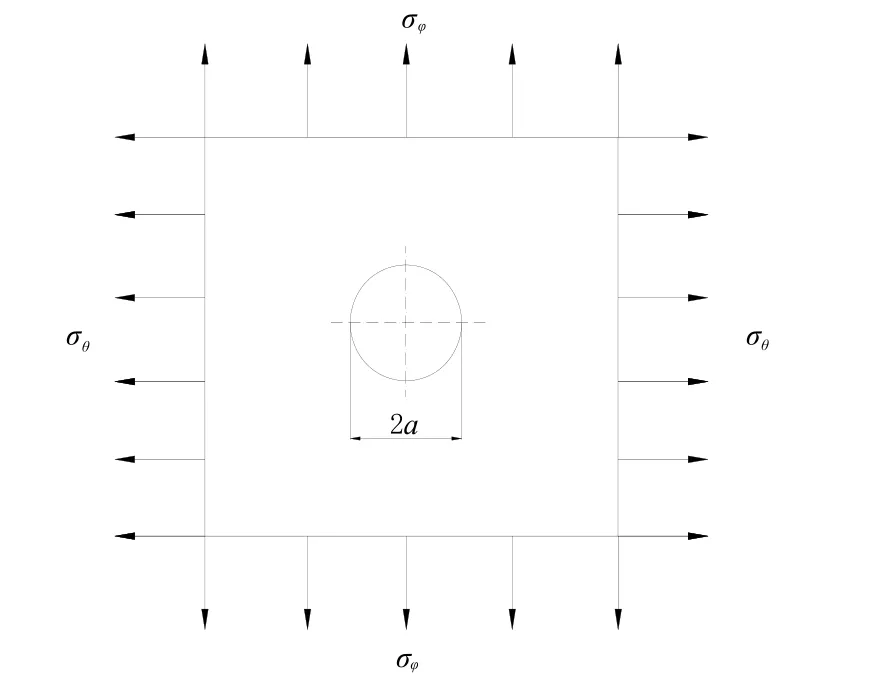
图2 受均匀内压圆柱壳上开小圆孔的应力示意图Fig.2 Stress about uniform internal pressure cylindrical shell with a small circular hole diagram

受内压薄壁圆柱壳上开小圆孔，在孔边处：

于是，此壳体的应力集中系数Kt=2.5σ/σ=2.5。

2.2 薄壁球壳开小圆孔的应力集中

中面半径为 R，厚度为 t的薄壁球壳受内压 p作用时，产生两向薄膜应力，分别为周向应力σθ=pR/2t和经向应力 σφ=pR/2t，则 σθ=σφ=σ。如图 3所示。

图3 受均匀内压球壳上开小圆孔的应力示意图Fig.3 Stress about uniform internal pressure spherical shell with a small circular hole diagram

受内压薄壁球壳上开小圆孔，在孔边处有：

于是，此壳体的应力集中系数Kt=2σ/σ=2。

3 结 论

（1）薄壁壳体开小圆孔时，孔边缘处周向应力最大。

（2）薄壁壳体开小圆孔时，垂直于拉伸方向的截面上产生3倍的拉应力，平行于拉伸方向的截面上产生1倍的压应力。

（3）圆筒上开孔比球壳上开孔危害大。因此，压力容器上开孔时，优先考虑在球形封头上开孔。

［1］ 余国琮.化工容器及设备[M].北京：化学工业出版社,1980.

［2］ 张礼敬，张明广.压力容器安全[M].北京：机械工业出版社，2012.

［3］ 王志文，蔡仁良.化工容器设计[M].北京：化学工业出版社，2005.

［4］ 朱晓东,覃启东.基于 ANSYS平台含圆孔薄板的应力集中分析[J].苏州大学学报（工科版），2004，24（5）：51-53.

［5］ 徐芝纶.弹性力学[M].北京：人民教育出版社，1979.

［6］ 郑津洋，董其伍，桑芝富.过程设备设计[M].北京：化学工业出版社，2005.