粒子群算法求解物流路径优化问题

何 泉

(监利县尺八镇初级中学，湖北 监利 433328)

1 物流配送路径优化问题描述

物流问题是当今最流行的运输优化问题，描述为：有n个客户点，最多使用m辆汽车，要求安排车辆行驶路线使车辆行驶总距离最少.并满足条件：

1)每个客户点的需求只能由一辆车来完成；

2)每个客户点需求量总和必须小于等于汽车载重量；

3)所有路径的长度总和必须小于等于单次配送行驶的最大距离。

2 粒子群算法

粒子群优化算法主要模拟鸟集群飞行觅食行为，每个粒子利用自身历史最优位置和整个粒子群的全局最优解提供的信息，在解空间内不断飞行，实现寻找最优解的目的。在基本PSO算法中，第i个粒子的飞翔速度是一个D维的向量，第i个粒子迄今为止发现的最好位置(个体极值),整个粒子群迄今为止发现的最好位置(全局极值),整个粒子群是通过个体极和全局极值来更新自己的飞行速度和飞行位置，在解空间中寻求最优解。c1和c2是学习因子,r1和r2是随机数。PSO算法每粒子采用如下公式来更改自己的速度和位置：

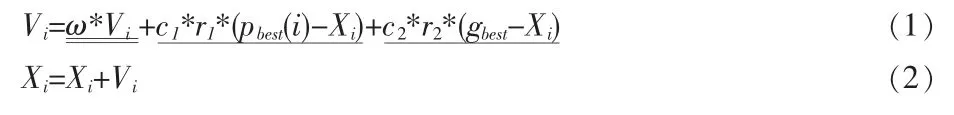
3 算法流程

步骤1：初始化种群规模、粒子的位置向量、速度向量，计算粒子的适应度；

步骤2：根据初始化粒子的全局最优值和个体最优值；

步骤3：并将粒子的pBest设置为个体当前最优位置，gBest设置为初始群体中整个粒子群体最佳位置；

步骤4：若算法满足收敛条件或达到最大迭代次数,则执行步骤7,否则，执行步骤6；

步骤 5：根据公式(1)和公式(2)求出粒子移动后的新个体最优和全局位置最优值；

步骤6：将迭代次数加1，并执行步骤3；步骤7：输出gBest，算法结束。

4 实验结果分析

某物流公司有一个配送中心，各配送点位置坐标和需求量如表1所示。

所有试验均在操作系统为windows 7，双核3.16GHz的Intel处理器和4GB内存，Matlab2010的平台上完成。连续计算50次，路线仿真图如图1所示，遗传算法和粒子群算法运行50次实验结果如表2所示。

从表2可以看出：PSO算法无论是从最优解、平均值、50次找到最优解次数还是平均计算时间均优于GA算法。实验数据说明PSO算法收敛速度快，对物流配送路径优化问题具有一定的可行性和有效性。

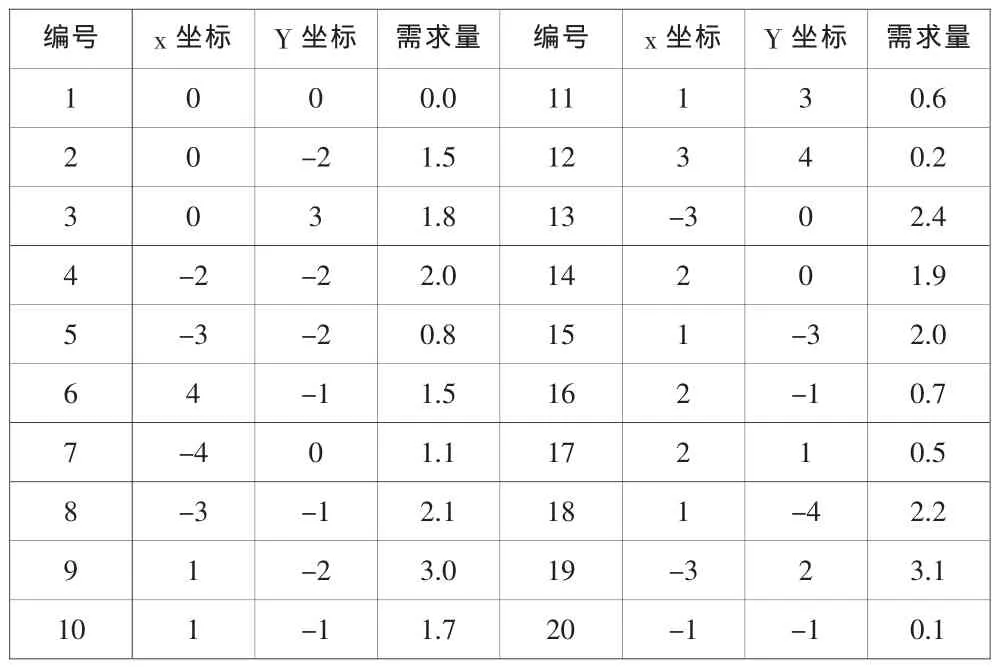
表1 各客户点到中心仓库的距

图1 CHCS算法路线仿真图

表2 算法运行50次结果

5 结论

针对物流问题的特殊性，提出了一种粒子群算法的物流车辆路径优化解决方案。仿真结果表明此算法，有效防止算法陷入局部最优解，加快了路径优化问题求解效率，并求得了最优解。可以用于解决寻求最优路径这一类实际问题。

[1]Kennedy J,Eberhart R.Particle swarm optimization[C]//IEEE Int Conf on Neural Networks.Piscataway:IEEE Press,1995:1942-1948.

[2]Azzawi A A G,Al-Saedi M A H.Face recognition based on mixed between selected feature by multiwavelet and particle swarm optimization[C]//Developments in E-systems Engineering(DESE).Piscataway:IEEE Press,2010:199-204.

[3]Wang fan,He xing shi,Wang yan.The cuckoo search algeorithm based on Gaussian disturbance[J].Journal of Xian.