显微镜下孢子彩色图像融合算法的研究
龙志林 杨永斌
(1.贵州高速公路集团有限公司,贵州贵阳 550003;2.中交第二公路工程局有限公司,陕西西安 710075)
1 概述
生物医学图像是图像处理的一大门类,应用范围非常广泛。现代电子显微镜的分辨率已经达到纳米级或更高,能用来观测分子甚至是原子的成像。在实际应用高倍显微镜观测时,限于样本制作技术,往往达不到这个水平,需要通过完善被观测样本的制造技术来提高观测效果。另外,采用先进的图像处理技术,也能够比较有效的提高观测效果[1]。计算机技术的快速发展,使得采用计算程序完成图像分析处理变得非常便捷,即图像融合技术,这类显微镜聚焦不清晰的问题也能够得到很好的解决[2]。
现代融合技术兴起于20世纪70年代[3,4],目前已广泛应用于医学图像处理等领域,以完成显微图像的处理。一般来说,在需要观测样品的景深较大的情况下,调整显微镜的焦平面往往只能观察到对应于该焦平面的部分清晰图像,而图像其他部分则会比较模糊。这种情况下,就需要在同一视场中,将不同的焦平面分别采集多幅图像,再运用图像融合技术对所采集的多幅图像进行融合处理,最后合成为完整的、每一景深部位均十分清晰的图像。
对多幅图像求平均是最简单的共聚焦显微图像融合算法,但效果也最不好。利用小波变换进行多聚焦图像融合是目前研究的一大热点,并已经达到较好的融合效果,但大多数算法都是针对灰度图像的融合。如果能在融合的同时保留住图像的彩色信息,这无疑更保障了后期目标物提取的准确性。文献[5]中提出了一种基于离散小波框架变换的算法,该算法可以比较好地融合两幅彩色图像。但是本文的研究对象是孢子彩色显微图像,对于同一场景如果仅仅采集2幅~3幅还是远远达不到预期的融合效果。在实际应用中,为了准确统计孢子的数量,对孢子图像的每一场景均采集了10幅图像。为了解决多幅显微图像的彩色融合问题,本文在传统的针对灰度图像融合算法的基础上,提出一种改进融合算法。该算法基于小波变换和高斯模糊,能够获得比较好的融合效果,而且还尽可能地缩短了融合处理所需花费的时间。
2 基于小波变换和高斯模糊的改进融合算法
2.1 传统的小波变换灰度图像融合算法
传统的小波变换灰度图像融合算法是利用两个一维滤波器实现对二维图像的快速小波分解,然后再利用两个一维重构滤波器进行图像的重构。如果f(x,y)表示一幅图像,则它的小波变换以离散形式实现。设定两个一维镜像滤波算子,H为低通,G为高通。r和c则分别对应于图像的行和列,原始图像f(x,y)为C0,按照这种算法,则在尺度j下有如下分解公式:

其中,h,v,d分别为水平,垂直和对角分量;J为分解层数;Cj为在尺度j下小波分解。相应的小波重构算法为:
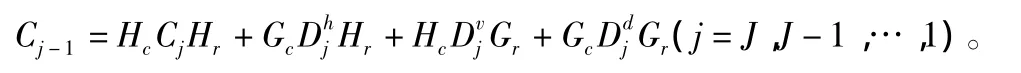
对二维图像进行N层分解,则可得3N+1个不同频带,其中高频带为3N个(记作LH,HL和HH)和低频带1个(记作LL)。以两幅图像的融合为例,说明这种图像融合算法的思路:
1)对于高频分量LH,HL和HH,则取两幅图像中相应系数矩阵中对应项的最大值。可以得到最强的边缘信息,从而获得质量良好的图像;
2)对于低频分量LL,考虑其对恢复图像质量的影响较大,一般采用下式进行计算:
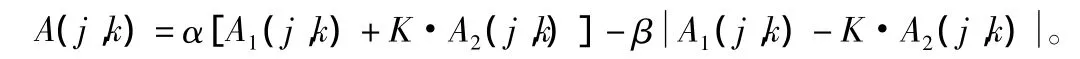
其中,K,α,β均为加权因子。公式前半部表示取两幅图像的加权均值,对融合后图像的亮度起关键作用;公式后半部分表示取两幅图像的加权差,包含两幅图像对应的模糊信息;K为调节两幅图像的占优比例因子,对两幅亮度不同的图像进行调节以达到均衡;α增大则图像加亮,β增大则图像的边缘加强。
这种融合算法能够尽可能地保留图像的细节部分,所以比较适用于灰度图像。在彩色数字图像中,如果简单地将上述的融合方法分别应用于R,G,B三基色上。在原图像的模糊区域,融合图像对应区域的图像质量得到提高,而清晰区域的质量则有所降低,另外这种方法所产生的方格效应也比较严重。在这里将其称为RGB融合法。
2.2 构造标准模糊图像
为了对彩色孢子图像进行融合处理而又不丢失彩色信息,可以采用像素的对等映射,即提取所有参加融合图像的清晰部分,融合成一幅最清晰的图像。要达到这个目标,首先需要构造一幅标准模糊图像,记作mol_f。本文通过小波变换和高斯模糊处理构造这样一幅图像。
1)小波变换。以往利用小波分析进行融合处理时,都是利用小波变换的金字塔结构以分离出图像的高频信息。其实低频信息也可以用于图像融合,这是一种求反的思想。
2)高斯模糊。在光学系统成像系统建模中,设定输入目标为f(x,y),输出目标为g(x,y),目标成像的作用则可表示为一个二维线性移不变系统,其光学系统对某个目标成像的冲激响应函数为 f(x,y),则:
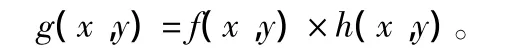
其中,h(x,y)为线性移不变系统对某个特定目标的成像效果。对于成像的某个特定目标而言,h(x,y)用一个高斯函数G(x,y,σ)近似,高斯函数σ的方差决定了光学系统对该目标的模糊程度。
本文为了进一步加强小波变换的效果,所以在小波变换后再进行高斯模糊处理。
3)改变彩色图像的色亮度和饱和度。如果用来生成标准模糊图像的原图像是最模糊的图像,这显然是最为理想的情况,但是实际上由于分块的区域不可能足够的小,所以这个目标很难实现。这时就要求所选用的原图像有一定的容错能力,即选为次模糊的一些图像时也能够比较准确地生成标准模糊图像。为了达到这个目标,需要改变所选源图像的亮度和饱和度。
3 改进的小波变换和高斯模糊的融合算法
本文对每一场景均取了10幅不同景深图像,记为fk。其中,k的取值是从1~10,分别代表这10幅源图像。
要用fk进行图像融合,首先要解决的问题是:如何在fk中选取最清晰的部分,原有的判定清晰目标和模糊目标的方法并不适合多幅图像。为了解决上述问题,本文首先需要生成给定场景下的一幅最模糊的图像作为标准图像mol_f(i,j),然后再用mol_f与fk分别进行比较,判定每一个像素点在哪一幅源图像fk上最清晰。
其次要确定清晰判定标准,本文确定的判定标准是:设最终的输出图像为out(i,j),则与标准图像某点mol_f(i,j)相差最大的就是最清晰的像素点out(i,j)。
4 融合结果及评价
为了评价本文的融合效果,分别采用本文融合法、RGB融合法和多图像求平均融合法,用matlab进行仿真处理以进行比较。
从理论上进行评价的结果见表1。

表1 融合效果评价
表1中,RMSE表示标准均方误差,其值越小表示融合效果越好;MI表示信息熵,其值越大表示融合效果越好;Pc表示正确率,显然其值越大表示融合效果越好。从表1中可以看出,本文算法的融合效果优于RGB融合法和多幅图像求平均法。
5 结语
以往的小波分析图像融合思路是通过小波算法获得最优的细节成分,这里则采用了相反的思路,即通过小波分析获取最不清晰的图像。另外,这里在小波分析之后又加入了高斯模糊,这一方面固然是为了增加模糊效果,但更重要的则是为了消除小波变换后的方格效应。而且本文的融合算法采用多幅图像,且融合后的图像是彩色的,通过仿真处理可以看到运算速度相对较快。
[1]夏德深,傅德胜.现在图像处理技术与应用[M].南京:东南大学出版社,1997:168-169.
[2]印敦国,李 勇.计算机图像分析处理技术在理化检测中的应用[J].工具技术,2003,37(5):46-48.
[3]何 友.多传感器信息融合及应用[M].北京:电子工业出版社,2000.
[4][美]Lawrence A.Klein.多传感器数据融合理论及应用[M].戴亚平.译,北京:北京理工大学出版社,2004.
[5]徐胜男,陈桂友,池 海.基于离散小波框架变换的彩色多聚焦图像融合算法[J].计算机应用,2005,25(3):580-582.

