GPS四参数 +高程拟合模型控制范围及其精度分析

郜怀龙

(中山华远国土工程有限公司，广东中山 528499)

当前，GPS定位技术已经被广泛应用，但GPS测量所用的坐标系是空间直角坐标系，是以地球质点为圆心，而城市测量大多采用54北京坐标或者地方坐标，因此就需要解决WGS84坐标与北京54坐标或者地方坐标相互转换的问题［1］，基于四参数+高程拟合法相对经典七参数法而言，条件较低，比较容易实现，通过分析该模型测量结果精度及控制区域范围［3］，并提出一些参考建议。

1 七参数转换模型及其精度分析

1.1 七参数矩阵形式

不同坐标系之间坐标转换在GPS测量中经常遇到，目前传统的坐标转换大多采用七参数线性模型，即三个位移参数(ΔX，ΔY，ΔZ)、三个旋转参数(Ex，Ey，Ez)和一个比例缩放因子(m)，对两个不同坐标系经过平移以及三次旋转，尺度改换，可以得到如下的公式:

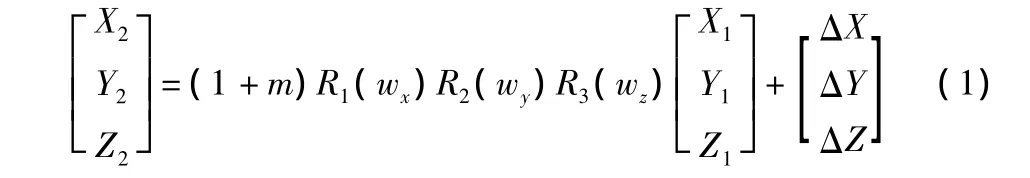
1.2 实验测区概况

下面以某工业区控制网为例，该控制网是由市国土资源局于2008年组织建成的城市D级控制网，南北距离15 km，东西距离15 km，基本上控制了该高新工业区的大部分区域。其中包括GT01，GT02，GT03，GT04，GT05，GT06，GT07，GT08，GT09，GT10 控制点(见表1)。

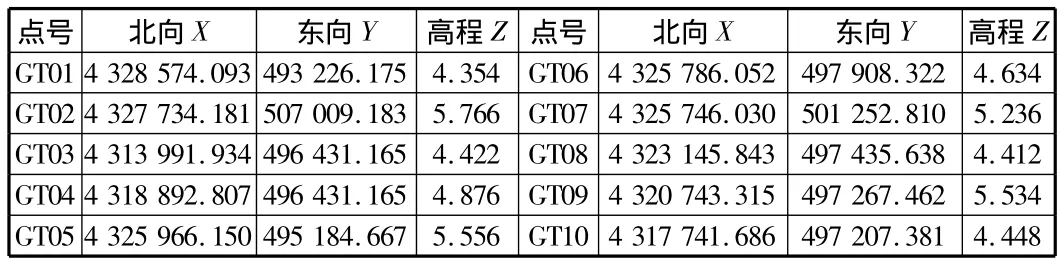
表1 某工业区控制点成果表

某工业区控制网点分布图见图1。

1.3 七参数应用及精度

因为七参数是求解两个不同坐标系之间的转换，所以需要知道同时在两个坐标系下的至少3个公共点，并且要求参与求解的公共点三维坐标精度要较高［5］。该高新工业区控制网点GT01，GT02，GT03，GT04 能够覆盖全区域，并且分布均匀精度高［4］，因此利用该四个控制点求取七参数。

设置移动站为RTK模式，同时设置中央子午线、投影参数并且输入求解得出的七参数，即可进入RTK固定解得出高精度的测量结果，然后对 GT05，GT06，GT07，GT08，GT09，GT10 进行测量，测量结果及误差对比见表2。

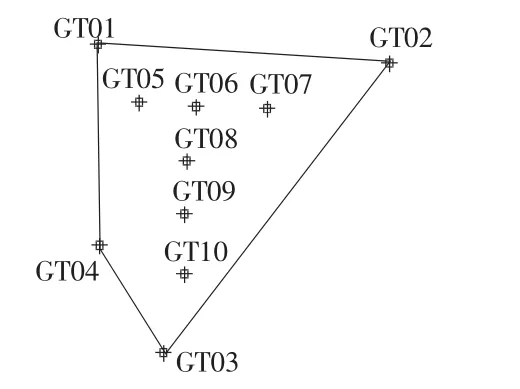
图1 某工业区控制网点分布图

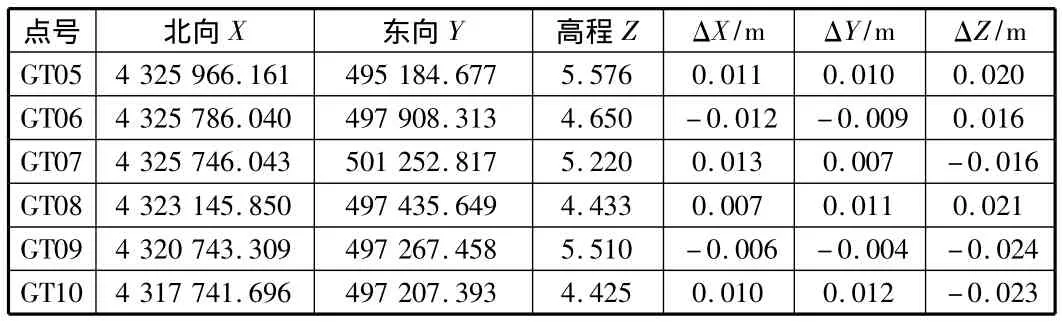
表2 测量点坐标及其误差

从坐标误差对比中可得 ΔXmax=13 mm，ΔYmax=12 mm，ΔZmax=24 mm，使用七参数所测得点坐标误差均符合城市测量规范要求。

2 四参数+高程拟合转换模型

1)四参数转换的基本思路。a.利用高斯投影正算公式及空间直角坐标与大地坐标的转换公式，将公共点的WGS84坐标和54年北京坐标分别在高斯平面上投影，然后计算得出这些公共点在高斯平面内的WGS84平面坐标和54年北京平面坐标。b.通过一组精度较低的参数计算，将其他点的WGS84平面坐标转换成54年北京坐标系下的近似平面坐标。c.计算坐标转换异常，即公共点上求出近似坐标减去其相应准确值。d.通过最小二乘方法解算转换异常场的平面四参数，最终求出WGS84平面坐标转换后精确的54北京平面坐标。

2)四参数模型及精度分析。GPSRTK测量的数据是WGS-84经纬度坐标，需要转换到城市测量坐标，这些都需要利用以上转换公式，GPSRTK中的坐标库可以完成以上计算。下面以某工业区控制网为例，并利用其中 GT01，GT02，GT03，GT04控制点求解四参数，然后利用求出的四参数测量其余控制点，四参数残差及测量结果见表3，表4。

由表3可得出通过GT01，GT02，GT03，GT04所求得的四参数残差较小，精度较高，利用四参数测得的控制点坐标 ΔXmax=16 mm，ΔYmax=15 mm，ΔZmax=26 mm，所测量点坐标符合城市测量规范。

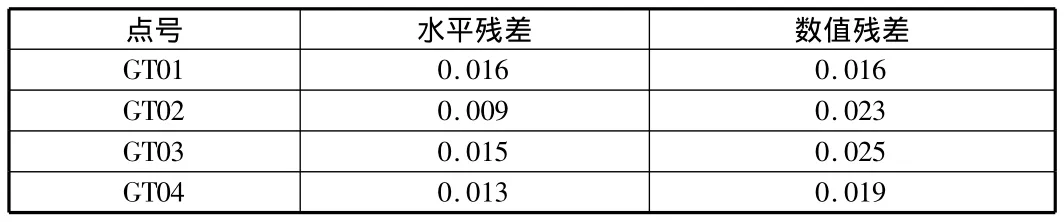
表3 四参数残差表 m

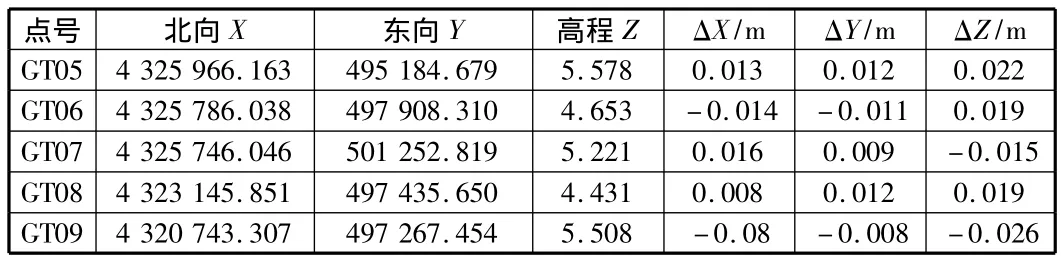
表4 测量点坐标及误差对比

3)高程拟合模型。GPS水准高程拟合方法是:通过对GPS网中一些水准点进行联测，利用这些点的大地高和正常高解算这些点的高程异常值，在已知它们的高程异常值与坐标位置的基础上，通过小二乘的方法拟合出测量区域的似大地水准面，用内插算法在似大地水准面上求出其他GPS点的高程异常［6］，从而获得各个未知点的正常高。很多数学模型用于GPS水准拟合，采用的数学模型不同或地形条件对不同所拟合的精度也不相同。

a.平面拟合(线性内插)。在小范围或平缓区域，可以把大地水准面相似于平面。此时，拟合大地水准面为:

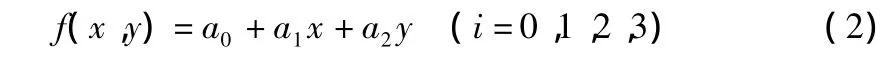
未知参数为a0，a1，a2，需要3个公共点才能解算。做四参数曲面拟合也即相关平面拟合，若选用公式第五项和前三项进行拟合，则曲面拟合表达式转换成f(x，y)=a0+a1x+a2y+a3xy，未知参数为a0，a1，a2，a3，这时4个公共点才能进行解算。

b.二次曲面拟合。拟合模型公式中的前六项，则曲面的拟合表达式为:

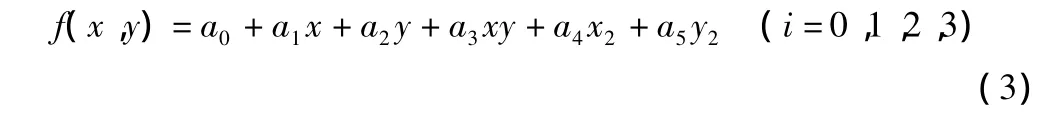
其中，a0，a1，a2，a3，a4，a5均为未知参数，这时 4 个公共点才能进行解算。这四种曲面拟合方法采用不同未知参数，并且其阶数也不同。

3 四参数控制区域分析

不同坐标系在同一椭球内进行转换即为四参数转换。以某工业区为例选取该工业区控制网点GT01，GT02，GT09参与解算四参数，该3个控制点覆盖了GT05，GT06，GT07所在区域的范围，没有覆盖GT03，GT04，GT10所在区域。通过实地测量对比分析不同区域控制点精度，控制区域见图2，测量结果见表5。

由图2，表5分析得出:在四参数所控制区域内测量的点坐标都控制在2 cm内，测量精度能够达到城市测量规范的要求，在控制区域外控制网点GT10距离控制范围3 km精度达到±2.5 cm，当距离增加至5 km时，测量GT04误差为±3 cm，当距离增加至8 km时，测量点GT03的误差达到将近4 cm。因此当测量位置距离参数控制区大于3 km时，精度不能够达到城市测量规范要求，应该重新求取参数。并且在15 km的控制区域内控制点若能够包围整个区域，所求取的参数能够达到城市测量规范要求。

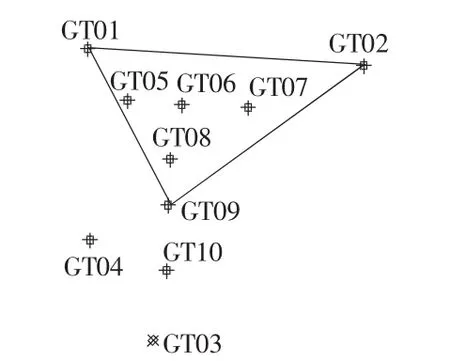
图2 控制区域图

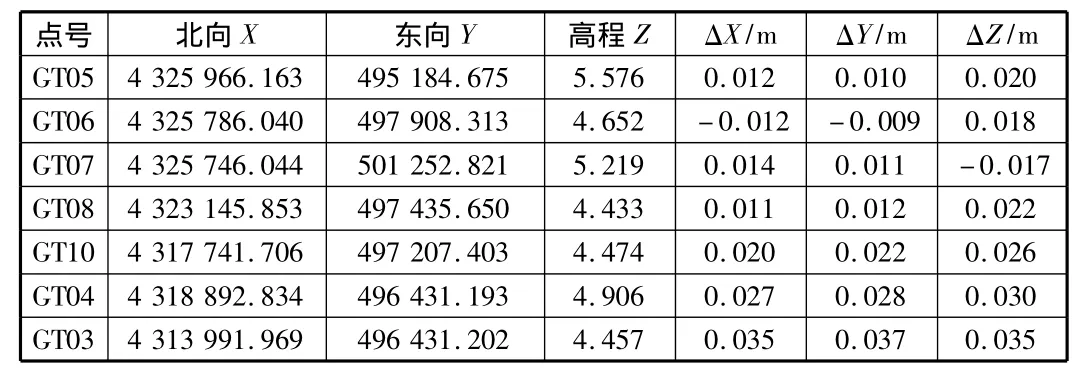
表5 控制网点坐标及误差

4 结语

通过以上对比分析，基于四参数+高程拟合坐标转换方法所需要的公共点个数较少，2个公共点也可以获得比较理想的转换参数，具有粗差探测能力，公共点存在明显的粗差，对最后的转换参数影响不显著，对公共点图形结构要求不高，同等精度的公共点组合可以不同，而结果类似。在工程测量或者地形测量中，测区范围在15 km以内，可以利用四参数代替七参数的测量方法，不仅提高了测量效率满足测量产品的可靠性，而且节约测量成本，并且使用该方法在京唐港国家级高新工业区多次完成了放线，测图等项目，为今后工程测量、地形测量人员提供实际借鉴指导。

［1］刘基余.全球定位系统原理及其应用［M］.北京:测绘出版社，1993:226-227.

［2］王解先，邱杨媛.高程误差对七参数转换的影响［J］.大地测量与地球动力学，2007，27(3):25-27.

［3］宋太广.GPS测量的误差源及精度控制［J］.测绘与空间地理信息，2008(4):31-32.

［4］唐力明，李成钢，张建国，等.GPS/RTK精密区域地表位移动态监测技术研究［J］.测绘通报，2010(5):1-2.

［5］王应东.GPS误差分析和精度控制［J］.测绘与空间地理信息，2011(6):43-44.

［6］张 勤，王 利.GPS坐标转换中高程异常误差影响规律研究［J］.测绘通报，2001(6):12-14.

［7］孔祥元，梅是义.控制测量学［M］.武汉:武汉测绘科技大学出版社，2000.