煤层气开采过程中储层压力变化预测

葛静涛，白雪静，陈 龙

（1.中国石化华东分公司非常规指挥部，山西 乡宁 042100；2.中国石化胜利油田鲁明油气勘探开发有限公司，山东 东营 257022）

煤层气与常规天然气的开采过程截然不同。煤层气的开采一般是通过排出地下水降低储层压力，从而使储层中吸附在煤基质表面的煤层气解吸出来，解吸出的气体在压力差和浓度差的双重作用下扩散、渗流运移到大的裂隙或井眼中，最终通过井筒采出地面[1]。流体在煤层中的运移规律决定了煤层气的开采特点，在煤层气开采中控制储层压力变化，随时了解储层压力的变化尤为重要。为此，本文建立了气、液两相流在煤层中运移规律的数学物理方程。

1 基本假设条件

1）溶解气气量忽略不计；

2）液体是微可压缩，煤层基质微可压缩；

3）考虑计算平面两相径向流一维模型；

4）在储层中流体运移过程中热交换量较少，可忽略；

5）煤层气解吸过程为瞬时现象。

2 割理系统中的渗流方程

2.1 气相渗流扩散方程

随着煤层气井地下水的不断采出，煤层中压力下降至煤层气解吸压力以下后，煤层气从煤中解吸进入割理中，在割理系统中，煤层气的运移主要遵循菲克扩散定律和达西渗流机制。与此同时，煤基质内部的气体不断解吸进入割理系统中，所以割理系统中气相应满足式（1）的质量守恒方程[2-4]：

式中

vg——割理中气体流速，m/d；

Bg——煤层气的体积系数，小数；

qg——日产气量，m3/d；

qmd——基质系统与割理系统的气体交换项，m3/（m3·d）；

Vm——煤基质中吸附气体的平均含量；

Ve——裂隙面上与自由气体压力处于平衡状态的吸附气体含量；

G——煤基质的气体扩散系数；

t——吸附时间常数，指当解吸气量占总气量的63%时所对应的时间[5]；

φf——割理的孔隙度，小数；

sg——割理中含气饱和度；

∇——哈密尔顿算子。

气体在渗流过程中服从达西定律，扩散过程中服从Fick第一定律，因此，割理系统中气体流速为扩散速度和渗流速度的和，考虑标准状况和煤层状况气体状态方程，整理得到割理系统中气相渗流方程的一般形式：

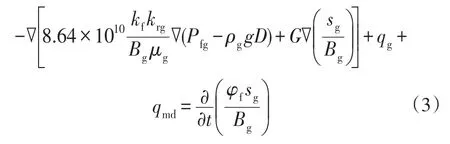
式中

kf——割理的渗透率，10-3μm2；

krg——割理中气体的相对渗透率，10-3μm2；

Pfg——割理中气体的压力，kPa；

μg——割理中气体的黏度，mPa·s；

ρg——气相密度，kg/m3；

D——煤层深度，m；其它符号同上。

2.2 液相渗流方程

液相在割理中以渗流的方式运移，因此，利用连续性方程和达西定律可以得出液相渗流方程的一般形式∶

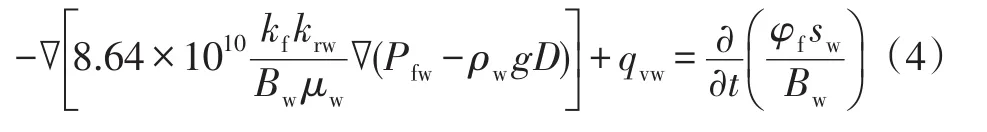
式中

krw——割理中液相相对渗透率；

Bw——割理中液相体积系数；

μw——液相黏度，mPa·s；

Pfw——割理中液相压力，kPa；

ρw——液相密度，kg/m3；

qvw——液相产量，m3/d；

sw——液相饱和度。

3 基质中煤层气渗流方程

煤层气的解吸特性可用吸附等温曲线或朗缪尔方程加以描述，煤层气在深度梯度的驱动下，通过孔隙向裂隙空间扩散。这一过程相当于一个匀布在基质表面的质量源对裂隙系统质量扩散，对于裂隙是流入，对于孔隙系统是流出。据Fick扩散方程描述基质系统中气体解吸运移过程，则得到如下方程：

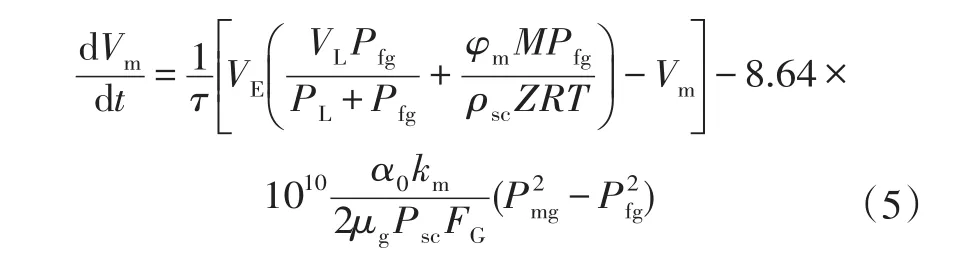
式中

Vm——基质单元内气相平均浓度，m3/m3；

VE——基质单元表面覆盖满单分子层时的气体浓度，m3/m3；

τ——煤层气解吸时间，d；

μg——基质内气体的黏度，mPa·s；

FG——几何相关因子。

4 数学模型求解

本文求解的两相流偏微分方程可简化为一维二阶径相渗流偏微分方程[6]：

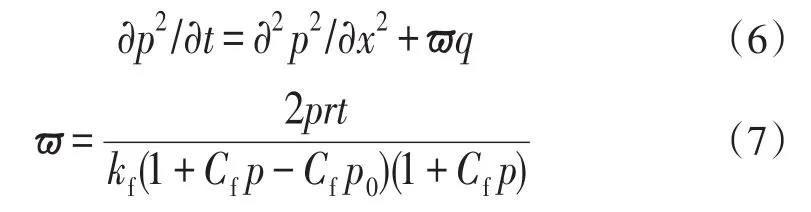
要求在不同生产时间下的煤层水平径向上各点的压力值，考虑L—T坐标构成的空间—时间网格系统，取空间步长ΔL=l，时间步长为ΔT=t，函数P的下标表示煤层于井底径向网格距离，上标表示时间。为了保证计算速度和计算结果的精度，本文采用古典隐式差分法求解煤层气一维渗流方程式。将式（3）、（4）、（5）简化整理代入式（6）得到差分后的格式，并对时间进行离散，其中压力和解吸运移扩散量采用隐式处理，产量项、重力和毛管压力以及扩散项采用上一时刻的值显示处理，整理可得到式（8）：

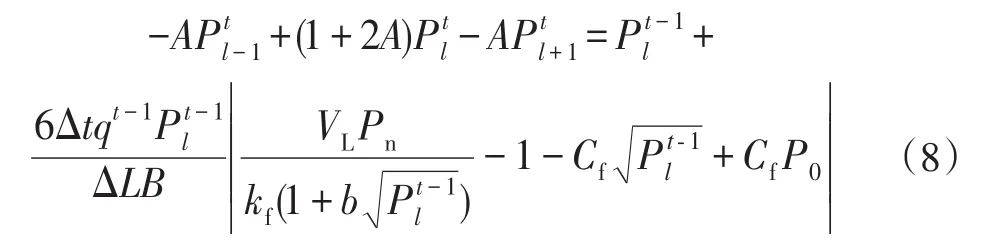
式中

VL——朗缪尔体积，m3/t；

b——吸附系数，是温度和吸附热的函数；

P——储层压力，Pa；

Cf——煤层基质可压缩系数，即煤层体积弹性模量的倒数，Pa-1；

φ——煤层孔隙度，分数。

对于无限大地层煤层气井生产时初始条件：

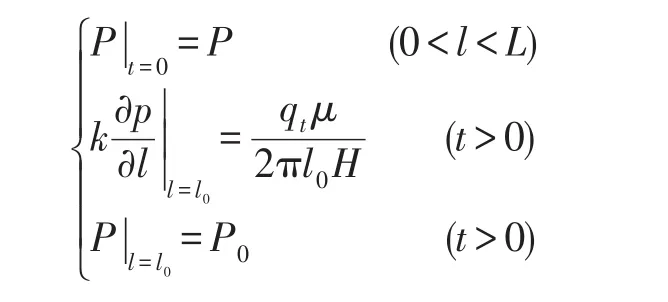
对有界封闭地层煤层气井生产时初始条件：

将式（7）写成矩阵形式：

YPt=Pt-1+Xt=1，2，…T系数矩阵Y为：

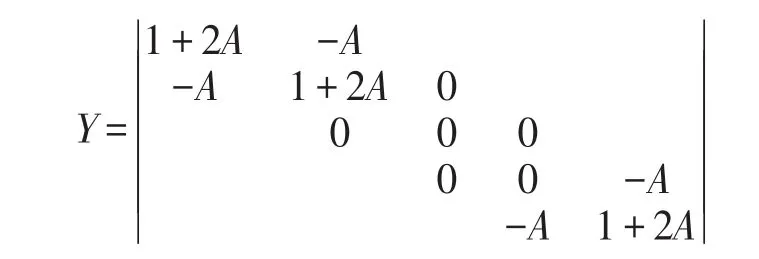
借助计算机编程，将煤层以井底为圆心，远离井底平面径向无限远处划分为L个网格，求每一时刻T天l处的煤层压力。在计算每一时刻网格内的煤层压力P值P1、P2、P3、…Pl-1、PL都要解矩阵Y，可以看出系数矩阵Y明显是主对角线元素严格占优，因此，对于每一时刻t方程组都存在唯一解。

5 实例分析

以山西延川南工区A井为例，基本参数选取如下：VL为朗缪尔体积38.29m3/t；P0为原始地层压力7.81 MPa；D为煤层厚度5m；μg为该井标况下气体黏度1.08×10-2mPa·s；Cf为煤层可压缩系数1.92×10-10Pa-1；φ为煤层孔隙度10.39%；K为煤层渗透率1.1×10-6μm2；Sg为气相吸附饱和度83.33%；解析压力0.792 MPa；气液体积系数，液相在不同温度、压力下的黏度可通过经验公式计算。

用以上基础数据采用本文所建模型，借助计算机程序可计算出不同时间下储层各位置的压力分布值，计算结果见图1。

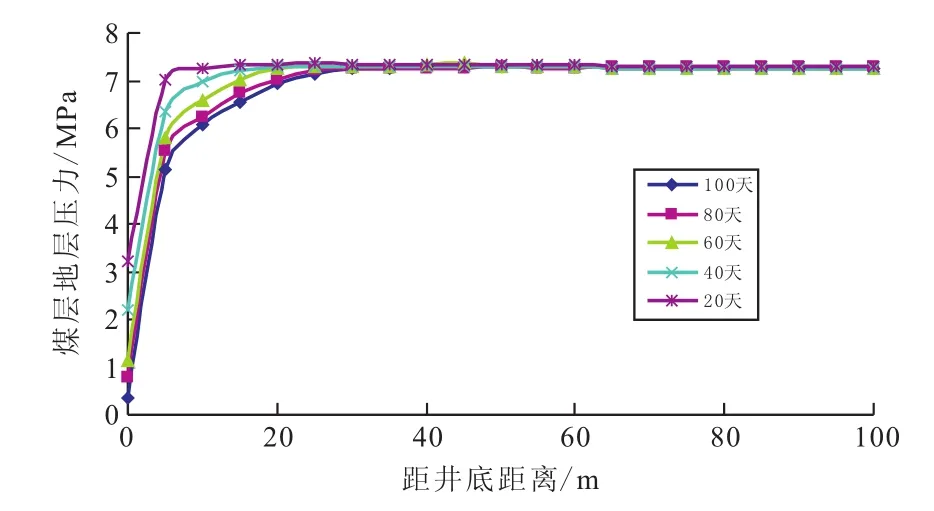
图1 排采时间与煤层地层压力变化曲线Fig.1 Variation curves of production time and coal formation pressure changes

图1描述了同一生产制度，不同生产时间下的煤层中地层压力的变化规律，曲线从左到右依次为生产20天、40天、60天、80天、100天后储层中压力分布。可以看出，随着生产时间的增加，井底流压即L=0时的储层压力，井底流压随着开采时间的增加，是逐渐减小的，近井地带的压降漏斗是逐渐增大的，而变化趋势随着生产时间的增大逐渐减小。这是因为在生产初期排水时期，煤层中只有水，为单相平面径向流，随着储层压力进一步下降，当下降到煤层气解吸压力以下时，一定量的气体从基质表面解吸，开始形成少量的气泡，这时煤层中为气液两相流，液相的相对渗透率下降，而随着流体的采出，储层压力也是逐渐下降，解吸半径不断增大，气体的解吸量增加。从计算结果还可以看出，日降井底流压越大，压降漏斗变化率越大，因为采出水过近井地带的储层压力下降太快，压降不能扩散更远，导致解吸半径过小，这一点也解释了煤层气生产中长期、缓慢、稳定的排采思想的正确性。

6 结论

将模拟计算结果与实际的生产数据相结合，借助计算机编程，应用所建的数学模型，对煤层气开采过程中煤层流体的运移进行数值模拟，可得出如下结论：

1）本文计算方法可以预测煤层压力场的变化趋势，模拟开采过程中在该产量下的井底流压和储层供气的供给半径变化。

2）同一口井，采用较缓慢的降压，地层压力下降较慢，近井地带的压降漏斗半径较大，排采中的排水降压效果较好，解吸半径大，但开采时间长。如果选择解吸前和解吸后的压降速率，需要在数值模拟计算的基础上，结合生产要求考虑经济效率来决定排采制度。

3）在解吸前后由于在数值模拟中是突然从单相流变为两相流，所以在计算地层压力变化率有突变的过程。而在实际生产中，煤层气解吸后需要解吸气量的积累，才能从地层中采出，因此，在解吸前后需要现场实时精确监控地层压力变化率，保证气体采出平衡解吸。

4）本文计算方法没有考虑人工储层改造技术对储层压力变化的影响，还需要更完善的数字模型来模拟储层压力的变化。在实际生产中还有煤粉和压裂砂对流体采出时的影响和长期排采后井间干扰等，都影响到模拟的准确度。因此，本文计算模型需要在煤层气生产中逐步完善，以便更好的预测储层压力的变化。

[1]贺天才，秦勇.煤层气勘探与开发利用技术[M].北京：中国矿业大学出版社，2007.

[2]傅广，吕延防.天然气扩散作用及其研究方法[M].北京：石油工业出版社，1999.

[3]王宏图，杜云贵，鲜学福，等.地球物理场中的煤层瓦斯渗流方程[J].岩石力学与工程学报，2002，21（5）：644-646.

[4]聂百胜，张力，马文芳.煤层甲烷在煤孔隙中扩散的微观机理[J].煤田地质与勘探，2000，28（6）：20-22.

[5]王晓梅，张群，张培河，等.煤层气储层数值模拟研究的应用[J].天然气地球科学，2004，15（6）：664-668.

[6]张力，何学秋，李侯全.煤层气渗流方程及数值模拟[J].天然气工业，2002，22（1）：23-26.