基于有限差分FLAC3D的边坡稳定分析及工程对策

韩 雪，安文博，赵子龙，杨文举

( 1．黑龙江科技大学建筑工程学院，哈尔滨150022; 2．中国化学工程第一岩土工程有限公司，河北沧州061000)

基于有限差分FLAC3D的边坡稳定分析及工程对策

韩 雪1，安文博1，赵子龙1，杨文举2

( 1．黑龙江科技大学建筑工程学院，哈尔滨150022; 2．中国化学工程第一岩土工程有限公司，河北沧州061000)

以鹤岗3052项目CE段边坡工程为背景，结合现场测试数据，运用有限差分法FLAC3D对边坡稳定性进行数值模拟分析，探究坡体发生变形破坏的原因及其影响因素，进而提出相应的工程对策。分析结果表明:边坡局部白浆土夹层遇水软化、抗剪强度大幅降低且形成边坡滑塌破坏潜在滑动面，是坡体发生变形破坏的主要原因;白浆土分布是边坡稳定性的主要控制因素。据此，后续工程建设应对白浆土的分布进行详实准确勘察，结合工程地质条件对白浆土分布集中区域坡体采用削坡减载法处理。

有限差分;边坡稳定性;白浆土;削坡减载

收稿日期: 2013-12-31
第一作者简介:韩 雪( 1969-)，男，吉林省榆树人，教授，博士，研究方向:岩土工程减灾，E-mail: hanxue69@ yahoo．cn。

我国幅员辽阔，地质条件复杂多样，滑坡、泥石流等灾害频发[1]。其中，由于人类工程活动引发的滑坡灾害也时有发生。因此，结合不同区域的工程地质条件，采用一定的方法和技术手段分析工程边坡稳定性，并据此采取相应的工程对策，对安全、经济、高效的工程建设具有重要意义。文中以鹤岗3052项目CE段边坡为工程背景，结合现场测试数据，采用有限差分数值模拟的方法，分析边坡稳定性及破坏原因，为工程建设提供科学依据。

1工程概况与地质特征

1. 1 工程概况

工程CE段边坡所处区域的地貌类型属丘陵漫岗，由于切坡后未对其进行相应的防护处理，切坡作业影响范围内的岩土体发生了大面积的变形破坏。

( 1)因植被揭除，坡肩至征地红线范围内的坡顶面在坡面片流与沟流的侵蚀作用下形成了大量的冲沟。

( 2)边坡坡面在应力释放与自身重力的作用下严重变形，形成上凸下凹的不平整坡面。

( 3)因崩塌、滑塌、冲刷作用形成的岩屑堆沿坡脚连续分布，在边坡的北段和南段先后发生了较大型的滑塌。坡体破坏情况如图1所示。

1. 2 边坡主要地层及岩性

工程CE段边坡区域地层主要为海相、海陆交互相和陆相沉积。在工程场区，边坡开挖出露的地层自上而下主要分层和岩性如下:

1层:素填土，灰黄～灰褐色，局部灰色，以黏性土为主，局部为粗砂、砾砂，夹植物根茎，结构松散。

2层:全风化砂质泥岩，黄褐色、灰白色，局部灰色，以风化的粉砂、粗砂、砾砂为主，矿物成分由石英、长石组成，颗粒呈亚圆形，密实。部分泥岩风化成土状，硬塑，局部可塑。

3层:强风化泥质砂岩，黄褐色、灰白色，局部灰色，风化成中砂、粗砂状，含泥质，局部风化成土状，属极软岩。

4层:强风化砂质泥岩，黄褐色、灰白色，局部灰色，以风化形成的土状为主，夹较多粉砂、粗砂、砾砂颗粒，岩芯呈短柱状，属极软岩。

3层和4层局部分布白浆土，边坡地层概况如图2所示。

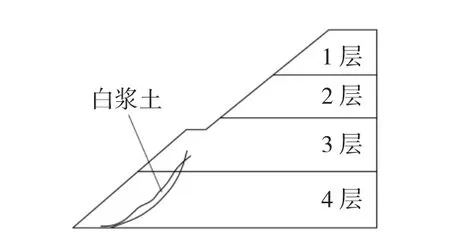
图2 地质结构分布Fig．2 Geological structure distribution

2 数值模拟

2. 1 有限差分法原理

有限差分法源于20世纪40年代，需要建立刚度矩阵，求出偏微分方程的“显示解”。其依据公式[2]空间导数的有限差分方程

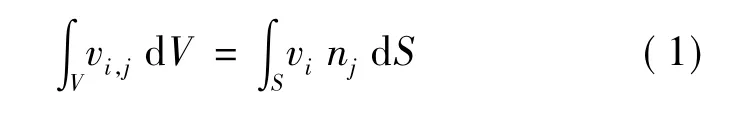
和节点运动方程、时间导数有限差分方程

进行有限差分，在时间及空间上进行运算。相对其他有限元原理来说，它能很好地解决大变形问题。有限差分原理利用混合离散技术，将空间物体划分为无数个六面体单元，通过节点之间的连接，建立关系式以计算有限差分时程方程。求解计算过程如图3所示[3]。

图3 求解过程Fig．3 Solving process

2. 2 模型建立

工程边坡实体原型抽象为数值计算模型，采用FLAC3D进行数值模拟，三维分析模型、网格及监测点布置如图4所示。

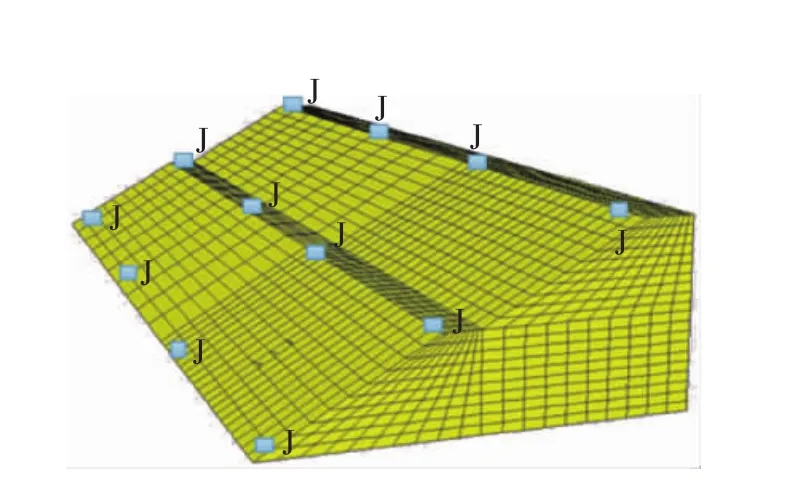
图4 边坡三维数值分析模型及监测点布置Fig．4 Slope three-dimensional numerical analysis model and monitoring point arrangement

坡段坡高h = 15. 5 m，坡底标高为±0 m，分析模型网格数为19 000，原型模拟范围为CE段边坡，长(与纸面垂直的y轴方向)×宽(与纸面平行的x轴方向)×高(垂直方向，即z轴) =100 m×60 m× 15. 5 m。模拟实验中，对于白浆土薄土层，将其简化为层理结构[4]，并在模型中建立了分界面。考虑雨水冲刷、渗透以及自重等作用，在施加外部荷载的过程中，采用强度折减法[5]，利用式( 3)、( 4)对强度指标参数进行折减。

式中: F——折减系数，又称边坡稳定最小安全系数;

φ——折减后摩擦角;

c——黏聚力。

模型边界条件，底部边界固定，左右垂直边界约束水平位移。

计算模型监测点与现场已设监测点采取对应布置。计算段共设置12个计算测点，测点沿边坡水平向间距25 m，沿坡面斜向间距约30 m。现场在部分相应测点位置按规程设有测斜孔，对该边坡重点部位的位移情况进行跟踪监测和对比分析。

根据工程勘察、现场测试和室内实验，模拟分析土层参数，指标取值见表1。

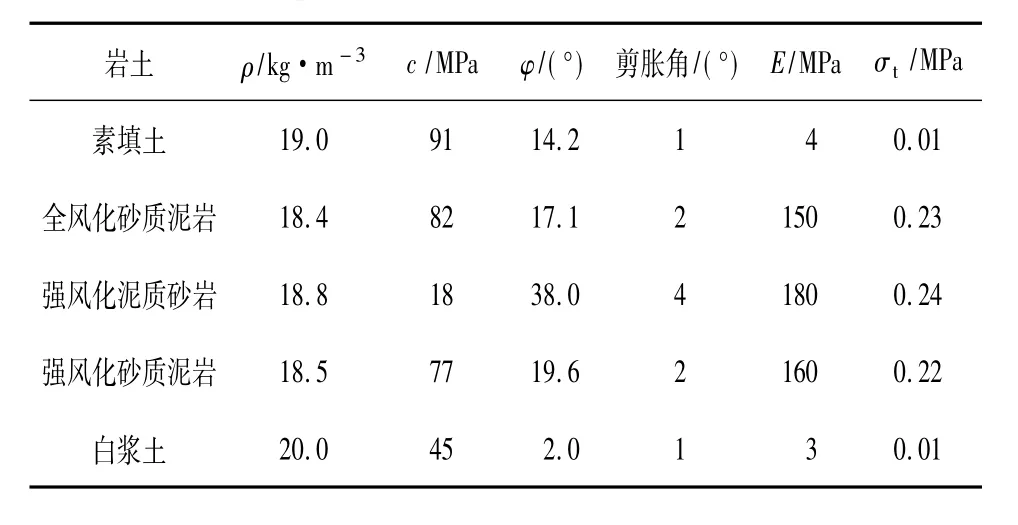
表1数值模拟中使用的土层参数Table 1 Soil parameters used in numerical simulation

3模拟实验结果分析

为研究白浆土薄弱层对边坡稳定性的影响，分别进行了不考虑和考虑白浆土弱化作用运算，就两种运算结果进行分析。

3. 1不考虑白浆土强度弱化作用

图5 和图6是不考虑白浆土强度弱化作用计算结果，分别为边坡x轴方向位移和应力云图。由图5可知，在y轴方向[16，34]m范围及附近区域，坡体局部产生了5. 5 mm位移。根据一般滑坡破坏机制[1]，坡体应出现微撕裂现象，进而形成裂缝。由图6可见，x轴方向应力分层，根据三轴应力(图7)分析，在y、z轴一定的情况下，x轴向主应力大小相异，土层具有产生相对运动的力学条件。

图5 边坡x轴向位移Fig．5 x axial displacement nephogram of slope

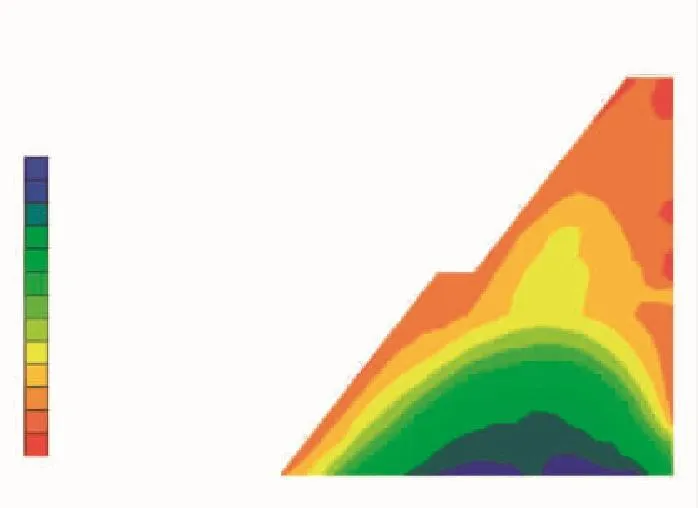
图6 边坡x轴向主应力Fig．6 x axis of slope to principal stress nephogram

图7 三轴应力Fig．7 Triaxial stress

图8 是不考虑白浆土强度弱化作用的边坡塑性区分布图。由图可知，坡体断面部分区域由弹性演变为塑性，并伴随出现拉伸屈服，坡体存在滑动破坏趋势。

图8 边坡塑性区分布( 16 m剖面)Fig．8 Slope plastic distinguish layout (16 m cutting plane)

3. 2考虑白浆土强度弱化作用

图9 和图10是考虑白浆土强度弱化作用计算结果，分别为边坡x轴方向位移和应力云图。

图9 边坡x轴向位移(考虑白浆土)Fig．9 x axial displacement nephogram of slope ( considering white paper clay)

由图9可知，y轴方向[16，34]m范围及附近区域，坡体局部产生了11 mm位移，白浆土强度弱化严重加剧了坡体位移。根据有关文献，在雨水及其渗透作用下，白浆土抗剪强度参数显著降低，最终将演变为滑移面[6-7]。

据图10可知，坡体表层x向主应力(与x轴负方向相同)由1. 0e4增大至2. 0e4，白浆土强度弱化作用使x方向上的应力显著增加，从而加剧了滑坡、塌落现象的发生。

图10 边坡x轴向主应力(考虑白浆土)Fig．10 x axis of slope to principal stress nephogram ( considering white paper clay)

图1 1是考虑白浆土强度弱化作用的边坡塑性区分布图。由图可知，坡体断面大部分区域由弹性演变为塑性，塑性区域进一步扩大;拉伸屈服特征也进一步明显，坡体滑动破坏特征显现。

图11 边坡塑性区分布( 16 m剖平面后面，考虑白浆土)Fig．11 Slope plastic distinguish layout ( 16 m behind cutting plane，considering white paper clay)

图1 2为现场J19号监测点位移曲线。此图形为不同深度位置累计位移量曲线，由图可知，现场监测孔的实测曲线数据与数值计算结果基本吻合。由于现场实测钻孔有限，对于实际测点不足的位置采用数值计算预测变形并采取相应的工程对策。

图12 J19测点水平位移(测斜)曲线Fig．12 J19 diagram of measuring points

4 工程对策

迄今为止，边坡治理主要有抗滑桩、锚杆、锚索、挡土墙、喷锚防护、削坡减载等方式[8-9]。其中，抗滑桩不宜用于软塑体滑坡，适于滑动面较深、滑动推力较大的情况。锚杆支护不宜用在深层滑坡，且在15 m之内应有基岩锚固，作为锚固支点。锚索支护不宜使用在滑面较缓的坡体。挡土墙的形式较多，其支护一般设置在滑坡体前缘，在使用时，需恰当设计挡土墙截面形状，以起到良好的效果。削坡减载法适用于塑性黏土、砂性土以及岩层。

依据数值分析结果，综合考虑工程地质条件和技术经济指标，防止3052项目边坡滑坡破坏，主要采取的工程对策如下:

( 1)进行更为详细的工程勘察，探明白浆土的分布情况;

( 2)对于顺层连续分布有白浆土的坡段，采用削坡减载的方法进行滑坡防治，修改设计坡体坡率为1∶2。

5结论

以鹤岗3052项目CE段边坡为研究工程背景，结合现场测试数据，采用有限差分FLAC3D数值模拟方法，分析边坡稳定性及破坏原因，并提出相应的工程对策，得到以下主要结论:

( 1)白浆土薄弱层的存在和分布特征是影响边坡稳定性的主要因素。白浆土具有遇水软化强度显著降低的特征。顺层连续分布有白浆土的坡段，在降雨等因素作用下边坡稳定安全系数显著降低。

( 2)工程勘察应详实准确探明白浆土的分布特征。顺层连续分布有白浆土的坡段，需要确定合理的坡率，采用削坡减载的方法进行滑坡防治。

[1] 黄润秋．20世纪以来中国的大型滑坡及其发生机制[J]．岩石力学与工程学报，2007，26( 3) : 433-453．

[2]孙书伟，林 杭，任连伟．FLAC3D在岩土工程中的应用[M]．北京:中国水利水电出版社，2011．

[3]金文佳．云南某露天矿岩质边坡结构参数优化研究[D]．昆明:昆明理工大学，2011．

[4]彭文斌．FLAC3D实用教程[M]．北京:机械工业出版社，2008．

[5] 陈国庆，黄润秋，周 辉，等．边坡渐进破坏的动态强度折减法研究[J]．岩土力学，2013，34( 4) : 1140-1146．

[6] 刘华磊，徐则民，张 勇，等．降雨条件下边坡裂缝的演化机制及对边坡稳定性影响——以云南省双柏县丁家坟滑坡为例[J]．灾害学，2011，26( 1) : 26-28．

[7] 刘婷婷，匡恩俊，高中超，等．白浆土某些物理性质的研究II．土壤抗剪强度及脆性[J]．黑龙江农业科学，2012( 5) : 40-43．

[8]高秋野．综合决策在边坡治理中的研究与应用[D]．青岛:山东科技大学，2008．

[9] 高 垠，王科峰，朱奎卫．复杂岩体边坡治理工程的综合加固措施研究[J]．岩土工程学报，2007，29( 5) : 760-764．

(编辑 晁晓筠)

Slope stability analysis and engineering measures based on finite difference method FLAC3D

HAN Xue1，AN Wenbo1，ZHAO Zilong1，YANG Wenju2

( 1．School of Civil Engineering，Heilongjiang University of Science&Technology，Harbin 150022，China; 2．China Chemical Engineering First Geotechnical Engineering Co．Ltd．，Cangzhou 061000，China)

This paper，drawing on the engineering background typical of CE segment slope collapse in Hegang 3052 project，describes the numerical simulation of slope stability using the FLAC3Dfinite difference method and combined with field monitoring data，the exploration of the causes and influencing factors triggering the slope deformation destruction，and the consequent application of the corresponding engineering countermeasures．The results suggest that the sharp reduction of shear strength produced by the softening of local soil interlayer in white pulp slope due to water，and the resulting occurrence of potential sliding surface of slope failure are mainly responsible for slope deformation and failure; the distribution of white pulp soil is the main factor controlling the slope stability．It follows that the further construction implies the necessity of achieving an accurate and detailed survey of the distribution of white pulp soil and controlling the slopes found in the areas with concentrated distribution of white pulp soil，by virtue of cutting slope and reducing load，as is dictated by actual engineering geological conditions．

finite difference method; slope angle optimization; white pulp soil; cutting slope lightening

10. 3969/j．issn．2095-7262. 2014. 01. 023

U416．14

2095-7262( 2014) 01-0103-05

A