基于GM(1，1)与灰区间估计的SPE通量水平长期预测

王中宇 李 强 燕 虎 王 倩

(北京航空航天大学 精密光机电一体化技术教育部重点实验室，北京100191)

太阳质子事件(SPE，Solar Proton Events)是日地空间爆发的一种强烈太阳活动[1－5]，其每次爆发都会产生大量的高能质子，这些高能质子会引起在轨运行空间站所在区域空间环境变化，影响空间站的通信、导航、电力以及空间试验等诸多领域，有时甚至引发在轨空间站关键部位控制功能的崩溃，造成巨大的经济损失[4，6－8];强烈的高能质子对宇航员的危害也不容小觑，短暂数分钟的高能质子辐射便会导致宇航员致盲，严重时甚至危及生命安全[1，3，7－9].预测太阳质子事件通量水平在长时间范围内的变化，便可以提前预知即将在轨运行空间站全寿命周期的空间环境状况，为空间站的防辐射及安全保护设计提供科学依据[4，7，9].

目前将通量大于10 MeV的粒子在连续15 min时间以内的数目超过10 cm2·s·sr的空间现象称为一个太阳质子事件.目前对于太阳质子事件的预测分为短期预测和中长期预测[1，3－4，7].短期预测一般提前1～10 d;中期预测提前半个或1个太阳自转周至几个月;长期预测提前1年或几年.预测类型的不同采用的方法有巨大差别，中、短期主要是依据预测因子数据来间接预测质子事件发生概率[2，5，8]，目前中、短期预测的研究相对较成熟;而长期预测主要是采用统计方法处理质子事件数据，进行定性预测(有、无预测)[4]，对其具体参数如对其通量水平预测较少.通量水平预测目前有3个类型:King模型、JPL模型和ESP 模型[4，6].King于 1978 年开发了第 1 个基于经验统计的太阳质子通量King模型[10]，鉴于极端SPE对总体样本的影响，King在进行通量数据统计处理时将其分离出来.JPL模型是用来预测太阳质子通量的标准模型，并且是目前最常用的计划航天任务模型[11－12]，该模型建立在理想假设的基础上:①除极端SPE外，SPE的通量服从对数正态分布;②不同太阳活跃年份质子事件的爆发频率是一致的.对于这两种假设目前争论较大.ESP模型是由NASA戈达得空间飞行中心(GSFC)开发的一种用于预测太阳质子通量和最坏情况下太阳质子事件模型，主要特点是将一般SPE通量的分布定义为一个截断的幂律形式[13－15]，忽视作为小概率的极端SPE.由于没有考虑极端质子事件的影响，以及SPE少数据的特性局限，以上3种模型所得预测结果都存在较大误差.

目前仍主要是从处理方法上着手来提高SPE通量水平预测精度，但是将极端SPE剔除的处理方式不合理;将极端SPE通量数据当作异常值予以剔除，不仅会减少有用的信息，而且造成预测精度偏高的假象.对已有SPE数据进行合理判断和区分，将极端质子事件与一般事件分开预测然后叠加合成最终结果，是获得较好预测结果的一个重要途径.

目前为止，人们对于SPE起因、质子加速、能量产生和传播机制等问题仍然没有定论;而且现有的SPE数据少，有资料记载的、可信的质子事件数据仅有253组，可以说SPE通量水平预测是一个典型的乏信息问题，很难用经典的统计学方法解决，而灰色系统理论在处理这类问题时显示出一定的优越性[16－17].本文综合灰色系统理论的GM(1，1)(Grey Model(1，1))与灰区间估计的知识，综合考虑一般SPE通量水平和极端SPE通量水平变化规律，提出一种实现乏信息条件下SPE通量水平的长期预测方法.

1 太阳质子事件长期预测

1.1 SPE通量灰色预测原理

GM(1，1)模型和灰区间估计是灰色系统理论的重要组成部分[16]，该方法不同于经典统计理论——不要求大样本量，允许概率分布未知，因此它更适合于解决少数据、贫信息和不确定系统的建模问题[16－17];而少数据、贫信息正是 SPE 通量预测问题的典型特征.

SPE通量水平的灰色预测原理是:首先对已发生的SPE通量数据进行甄别，识别出一般SPE和极端SPE，对一般SPE通量数据进行年均值化处理、对极端SPE通量数据进行对数化处理.然后分别建立以时间为序的一般SPE通量年均值序列和极端SPE通量对数化序列;以模型接续法分别对两个序列进行处理，生成各自动态模型序列，对各自序列进行一次累加生成、紧邻均值生成，得到灰微分方程，解方程得到系数估计值.最后对各个序列所得到的方程系数进行比较，得到最大、最小系数，依据所得系数建立上界、下界预测函数;极端SPE由上下界函数得到预测区间边界值;一般SPE，需结合SPE调节系数，生成一般SPE分量预测区间;将一般SPE分量预测区间与极端SPE分量预测区间叠加合成，生成最终预测结果.SPE通量水平灰色预测的详细原理如图1所示.

图1 SPE通量水平灰色预测原理Fig.1 Grey prediction principle of SPE’s flux levels

1.2 SPE通量灰色预测的具体实现

依据SPE类型的不同，将已发生的SPE通量水平数据进行年均值化或对数化预处理;对于没有极端SPE的年份，其对数化后的结果按0处理;然后依据预处理后的通量数据建立一个以发生年份为序通量序列为

对式(1)所得序列进行模型接续合成，该方法首先将SPE通量原始数据序列按照时刻划分成时刻子序列，并分别建立相应的时刻模型.时刻模型的第1位数据与原始序列的第1位数据相同，则将原始序列的第1位数据与其他各个时刻模型的第2位数据依次连接构成合成序列，合成序列如式(2)，所得结果如图2所示.

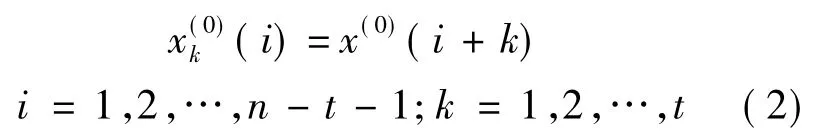
式中k为合成序列中数据的序号.

下面以X数列为例进行讲述.对X数列进行一次累加生成，得到一个非负递增序列x(1):

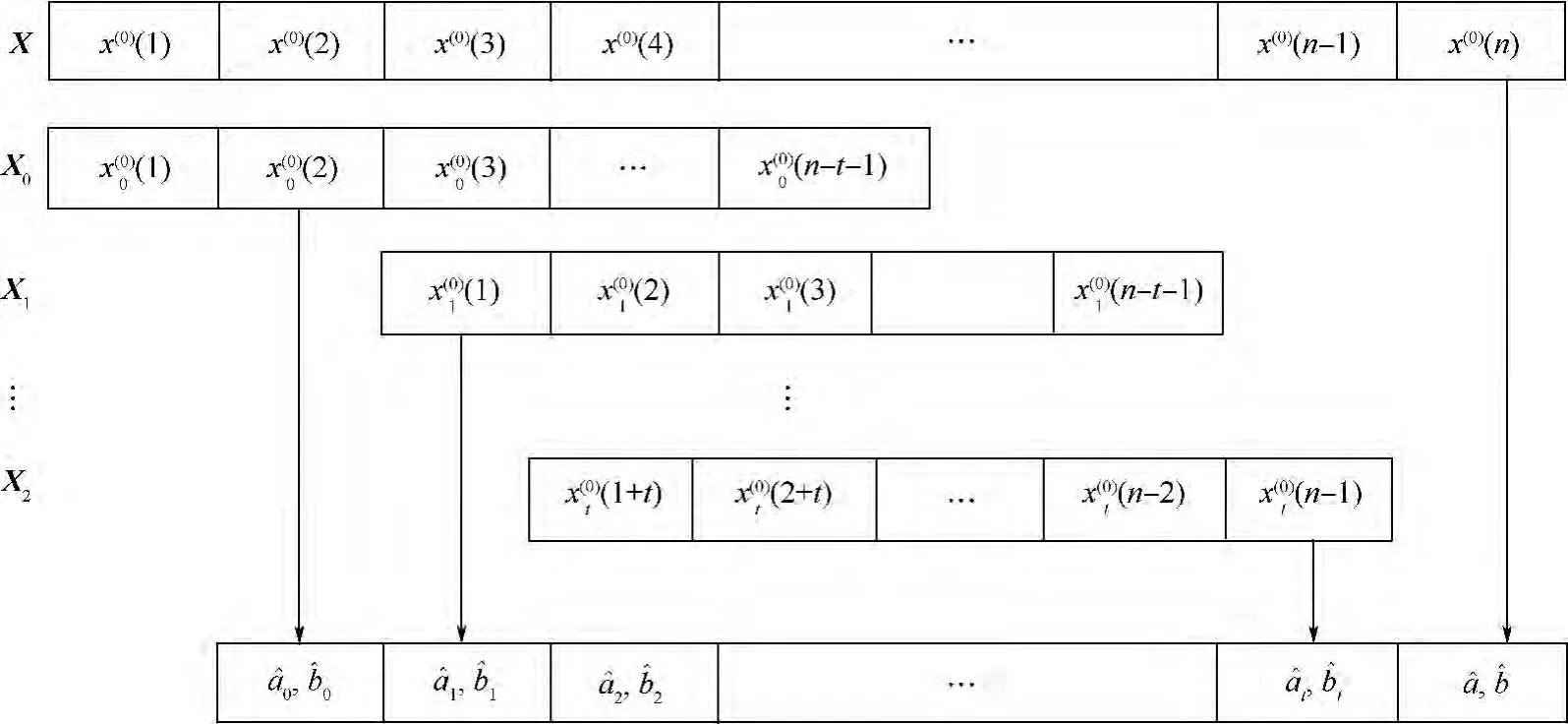
图2 SPE通量原始数据序列的模型接续合成Fig.2 Modeling approach of primitive flux sequence of SPE

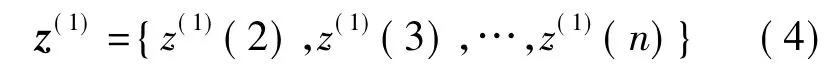
式中

至此利用得到的原始序列值和紧邻均值生成序列值构建SPE通量的灰色微分方程为

式中，a为发展系数;b为灰作用量，统称为辨识参数.

将式(5)所示的灰色微分方程用矩阵形式表示为

式中

式(6)为n－1维二元超定方程组，其中Y和φ为已知量，θ为系统的辨识参数.

求解式(6)超定方程组，可得θ的最小二乘估计值:

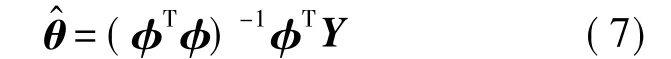
依照X数列处理方法，分别计算数列X0，X1，X2，…，Xt所建立灰色微分方程系数估计值.

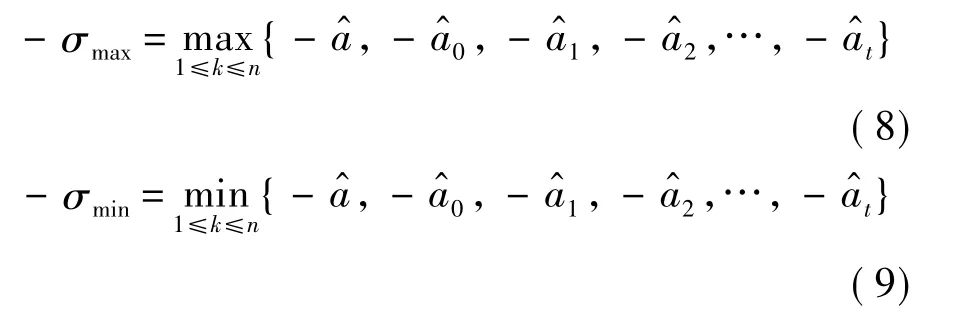
设序列x(1)的上界与下界函数分别为fs(n+t)和fu(n+t)，其表达式可分别表示为式(11)与式(12).以上界函数为例，则有n时刻的时间响应上界序列为(设σmax=at)

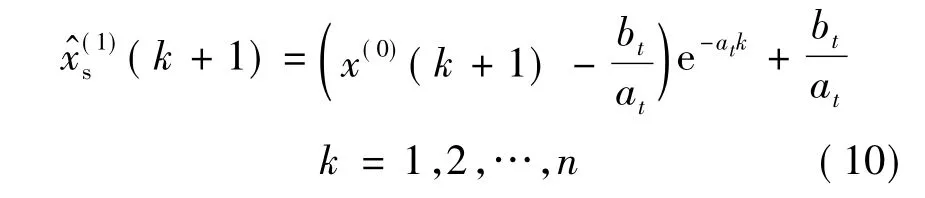
类似可以得到预测区间的下界为

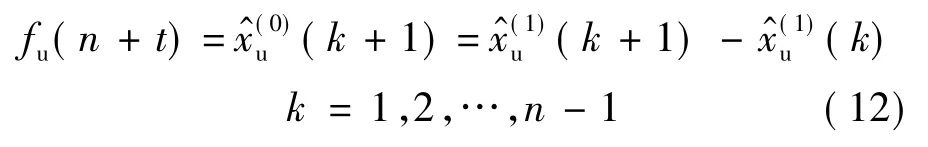
对于极端SPE，其预测间即为

一般SPE的预测区间则需要进行活跃性处理.

一般SPE由于存在一个10～11的交替活动的周期性变化;通常认为太阳活跃年持续7 a，并且活跃极大年的前2.5 a到后4.5 a，并依此作为判断 SPE 趋势的重要指标[2，4－7，10];另外在活跃性不同年份，SPE的通量分布具有显著弥散性.为了反映这些特性，本文提出一种刻画这类特性对活跃年份趋势变化影响的指标——SPE活跃性调节系数l，如式(13)所示，活跃极大年l=1.

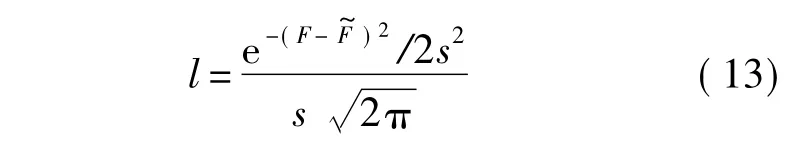
基于一般SPE的上界值(式(11))与下界值(式(12))，结合相应的活跃性调节系数，即可得到一般SPE通量预测区间:

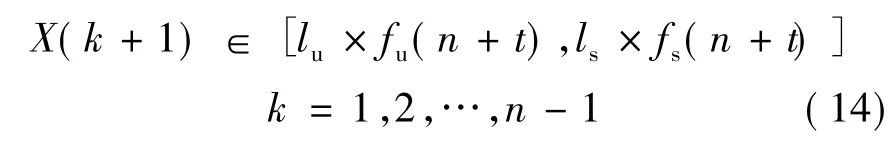
最后将一般SPE通量预测区间与极端SPE通量预测区间进行叠加合成，即得到预测年份通量水平.

表1 不同通量水平所对应的sTable1 The s corresponding to different flux levels

2 预测分析

2.1 SPE通量数据分析

为验证所提出SPE质子通量预测方法的有效性，选取1976—2012年发生的有记录的253次SPE数据，并将SPE数据以发生时间为序进行排列，图3为选用的SPE通量数据;从图3可以看出，多数SPE 的通量水平介于[10，500]MeV，称其为一般SPE，该类SPE占据已发生SPE数目的80%以上，少量介于[500，45 000]MeV，称其为极端SPE，该类SPE数量不足50个，从图3可以发现，极端SPE年际分布极为不均，具有集中爆发效应.

SPE的分布不均性也体现在发生数量上，图4为已发生质子事件数按发生时间的分布图，从图4可看出，除极端SPE，SPE事件爆发数量具有规律性变化趋势，呈现出一个大约11a的周期性;本文通过设置SPE活跃性调节系数反映这一特性对一般SPE的影响.

另外从图4还可以看出，极端SPE主要集中在[1978，1982]，[1989，1994]和[1998，2006]3个年份段，该时间段占据了极端SPE数目的94%，这种数量极少、能量极大的极端SPE具有很强的群聚性，普遍认为它已经突破了一般SPE运行规律;由于已知极端SPE样本小、信息少、单个事件的通量极大，为了减小极端SPE对预测的影响，JPL与King模型选择的处理方式是将这类极端SPE数据剔除，这种处理方式会减少有用的信息，做法具有不合理性.已发生极端SPE与一般SPE数据作为该类事件的表征，缺一不可;本文将一般SPE与极端SPE分离分开处理，分别预测各自通量分量，通过叠加合成方式生成最终结果，完整还原两类SPE因素对通量水平变化的作用.

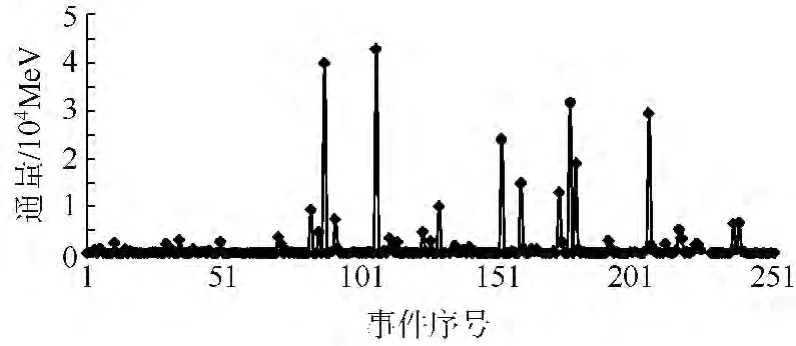
图3 1976—2013年5月发生的所有SPE数据Fig.3 Flux levels of SPE occurred from 1976 to May 2013

图4 SPE的年份分布Fig.4 The total of SPE occurred in every year

2.2 通量水平预测合成中的一般SPE分量

图5为分离后的一般SPE样本数据，滤除极端SPE后，1976—2013年有SPE事件发生的年份为31个;对同一年份的SPE通量数据进行均值化处理，得到一个年SPE事件通量均值化数列，其值变化如图6所示.从图6可以发现，一般性的SPE在3～4 a内呈现出相同变化趋势，并且在变化趋势发生改变时，其通量波动幅度较小，一般小于30 MeV，这些特征都是极端SPE不具备的.

下面以一般 SPE通量预测为例，结合以1976—2010年数据，对预测过程进行详细讲解，分别对2011年和2012年的SPE通量水平进行预测.X为剔除极端SPE数据后所得年均SPE通量所组成的原始数据序列，X0，X1，X2，X3和 X4为基于X所组成的合成序列.

图5 一般SPE通量水平Fig.5 Flux levels of normal SPE

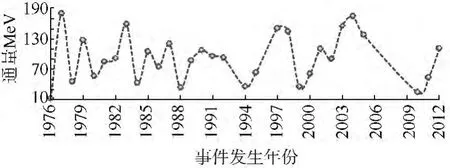
图6 SPE年通量的均值化Fig.6 Mean value of SPE’s flux levels in a year

对 X，X0，X1，X2，X3和 X46 个序列分别进行一次累加生成，得到递增数列，然后分别建立白化方程(即GM(1，1)模型):

估计参数得

又因为

故发展带上界序列响应公式为

由于上式是由X4序列得到，由此可得2011年与2012年最高预测值为

同理可求得发展带下界序列时间响应公式:

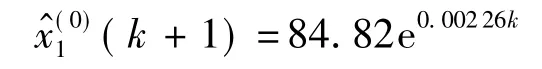
上式由数列 X1得到，由此可得2011年与2012年最低预测值为

根据太阳活跃周期律，可以得出2011年处在活跃年份，活跃性处于急剧变化状况，而2012年已经进入活跃极大年，活跃性达到峰值.依据式(14)并根据计算的初步通量值，从表1中选取相应的 s，计算2011年预测区间的 SPE活跃性系数:

依据SPE活跃性指标，2012年为活动极大年，因此SPE活跃性系数为:lu2012=ls2012=1.

根据式(14)可得2011年SPE通量水平预测区间为:[47.074，56.396]，2012 年为:[90.976，113.794].为了进一步验证方法的可靠性，同理，运用1976—2010年间数据，分为5个批次，预测已发生年份SPE通量水平，预测年限为未来2～3 a不等，所得结果如图7所示.

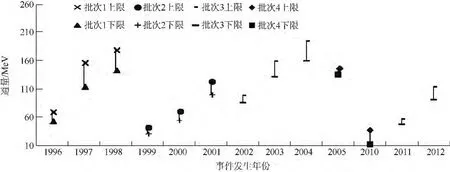
图7 一般SPE多年多次预测结果Fig.7 Predictions of normal SPE’s flux levels for many batches in many years

图7中标注批次1为运用1976—1995年间SPE数据预测1996—1998年SPE通量水平情况;批次2为运用1979—1998年间 SPE数据预测1999—2001年SPE通量水平情况;批次3为运用1981—2000年间 SPE数据预测 2002—2004年SPE通量水平情况;批次4为运用1985—2004年间SPE数据预测2005年和2010年SPE通量水平情况;批次5为运用1986—2010年间SPE数据预测2011年和2012年SPE通量水平情况.从图7中可以发现，单批次的预测区间随预测年限增长而变大.

2.3 通量水平预测合成中的极端SPE分量

图8为1976—2012年间发生的极端SPE通量数据，从图8可以看出极端SPE其通量水平介于[500，45000]MeV 之间，SPE 通量相差大，最大通量差异可达10倍以上.

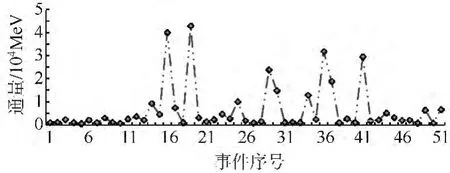
图8 极端SPE通量水平Fig.8 Flux levels of extreme SPE

为了弱化巨大差异的影响，使用对数方式对极端SPE通量数据进行预处理，然后计算各年的通量均值;对于没有极端SPE发生的年份，设定其预处理后结果为0.图9为极端SPE通量水平对数化年均值化后的结果，从图中可以看出，经过对数化年均值化处理后，非零通量值介于[2.8，4]MeV之间，预处理后极端SPE通量数据变化趋于平缓，这对预测是极为有利的.

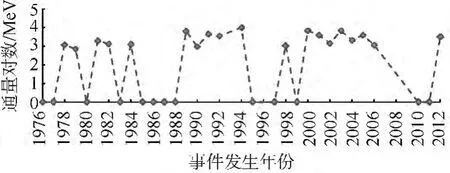
图9 极端SPE通量水平对数化年均值化结果Fig.9 Logarithmic and average flux levels of extreme SPE in every year

结合图9所示数据，分为5个批次，分别运用图9中1976—1995年间极端 SPE数据预测1996—1998年极端SPE通量水平情况(即图10中批次1);运用图9中1979—1998年间极端SPE数据预测1999—2001年极端SPE通量水平情况(即图10中批次2);运用图9中1981—2000年间极端SPE数据预测2002年和2003年极端SPE通量水平情况(即图10中批次3);运用图9中1985—2004年间极端SPE数据预测2004年和2005年极端SPE通量水平情况(即图10中批次4);运用图9中1986—2009年间极端SPE数据预测2010—2012年极端SPE通量水平情况(即图10中批次5).

图10为极端SPE通量数据经过灰色GM(1，1)与灰色区间估计处理后所得多年多批次预测结果，图中所得通量结果是经过对数还原的;从图10可以看出，2000年、2001年、2003年、2005年和2012年的SPE通量值较大，说明极端SPE主导着这些年份的通量变化;从图10还可以看出，对于没有极端SPE发生的年份，经过处理后所得通量值极小.

2.4 预测结果的合成

图11为一般SPE与极端SPE所得结果的叠加合成，可以看出，1996—2012各年实际通量均值水平均位于合成区间内，说明本文所提出的方法是正确的，将一般SPE与极端SPE分开处理结果叠加合成的处理策略是合理的.

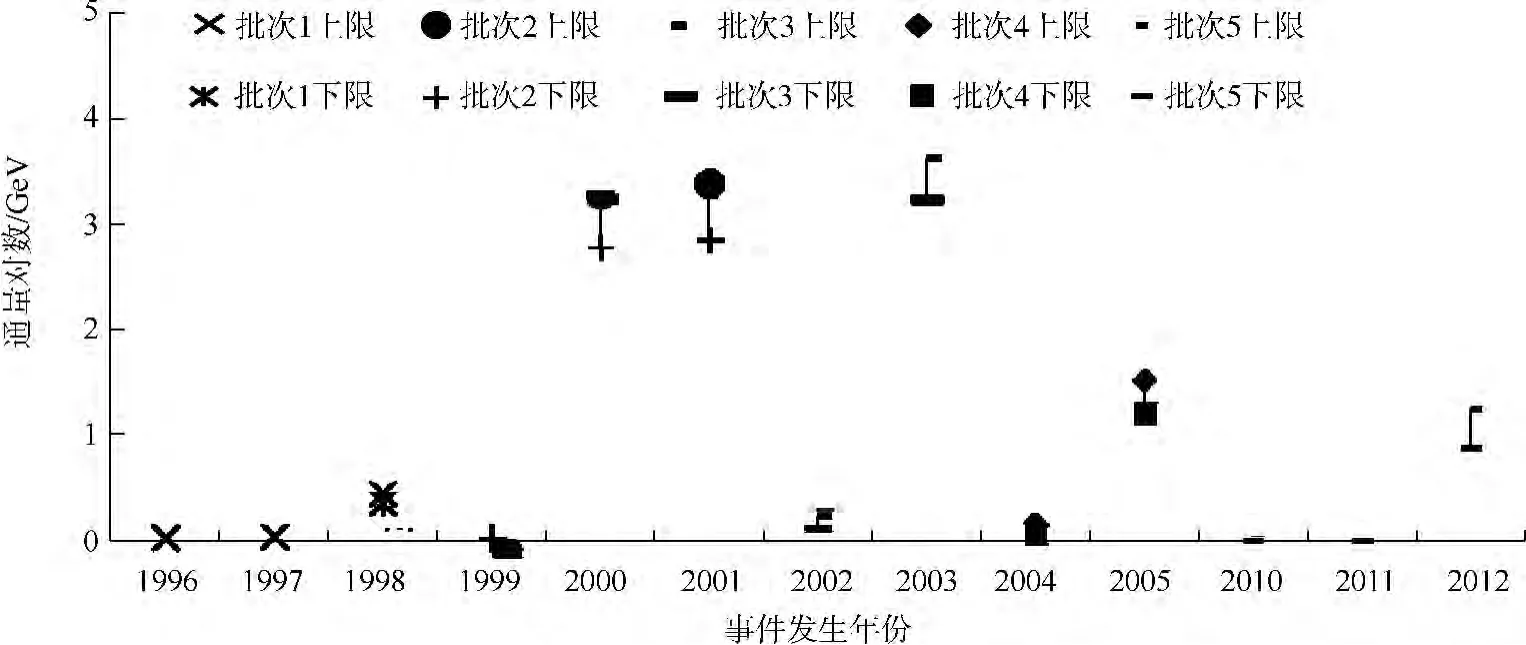
图10 极端SPE多年多批次预测结果Fig.10 Predictions of extreme SPE’s flux levels for many batches in many years

图11 叠加合成的预测结果Fig.11 Composed predictions of flux levels of extreme SPE and normal SPE

将一般SPE所得结果称为一般SPE结果分量，极端SPE所得结果称为极端SPE结果分量，将图7(一般SPE所得结果)、图10(极端SPE所得结果)及图11(叠加合成结果)对比后发现，对于没有极端SPE发生年份，一般SPE结果分量对其最终的结果合成起主导作用(如图11的1996年、1997年、1999年和2004年等)，而对于有一定数目极端SPE发生且通量水平较大年份，极端SPE结果分量主导着该年份的通量变化(如图11的2000年、2001年和2003年等).这里的结果也说明部分SPE通量预测模型(如JPL与King模型)将极端SPE数据剔除的做法是不合理的.

通过分析图11所得各年的通量预测区间，发现1996—1999年、2002年、2004年、2010—2012年的预测区间最大偏差小于27.43%，且这些年份实际发生的SPE有一个特征——通量水平较低;2000年、2001年、2003年、2005年和2012年预测年限内的预测区间最大偏差小于20.35%，通过查看图4数据可以发现，2000年、2001年、2003年、2005年和2012年这几个年份均有一定数目的极端SPE发生.

上述结果表明，在极端SPE发生年份，由于通量水平较大，如果预测算法稳定，反而可以取得较好的预测精度.

另外通过分析图11中各年预测偏差发现，一般SPE通量预测与极端SPE通量预测合成的预测结果随着各自预测年限的增长，包含实际值的预测区间有增大趋势(即偏差增大);如一般SPE通量预测与极端SPE通量预测的批次1均预测了1996—1998年3 a内的SPE通量水平情况，经计算，1996年合成结果的实际偏差为19.67%，1997年合成结果的实际偏差为22.36%，1998年合成结果的实际偏差为25.87%;一般SPE通量预测与极端SPE通量预测的批次2均预测了1999—2001年3 a内的SPE通量水平情况，经计算，1999年合成结果的实际偏差为16.51%，2000年合成结果的实际偏差为18.13%，2001年合成结果的实际偏差为20.35%.因此，综合考虑偏差和预测年限因素，一般SPE通量预测与极端SPE通量预测的单次预测时长以2～3 a为宜.另外，单从偏差数据上看，本文所提预测方法所得精度不高，但相比较目前著名的King模型和JPL模型而言，它们仅是对SPE通量水平出现在一个量级上的预测，所得结果变化范围大，而本文所提出的方法能将预测年份的通量值缩小到一个狭小区间，这显然更有价值和意义.

3 结论

鉴于SPE产生的机理和特点，本文在灰色GM(1，1)模型与灰区间估计的基础上，将SPE通量水平预测问题分解为一般SPE通量预测与极端SPE通量预测，结合反映一般SPE弥散特性的活跃性调节系数，提出了一种SPE通量水平灰色预测新方法并建立了模型.

1)文中运用了1976—2012年间发生的质子事件数据，分多批次预测1996—1998和1999—2001等年间SPE通量均值区间，结果表明各年实际发生SPE的通量均值均位于预测区间内，并且多年预测区间偏差最大值小于26%;另外实验结果还表明单次预测时长以2～3年为宜.

2)将SPE通量水平预测问题分解为一般SPE通量预测与极端SPE通量预测，之后叠加一般SPE结果分量与极端SPE结果分量合成所预测年份的SPE通量水平，该方法完整地利用了已有SPE通量数据信息，克服了SPE基于大样本统计预测方法的局限性和少数据的约束，预测效果较好.

3)本文所提的建模方法所需SPE通量样本量少，对通量数据的分布状况无要求;模型采用了灰色新陈代谢的思想，建立通量随时间变化模型序列代替单一模型，使模型具有动态性，可以很好表征SPE通量水平周期性变化中的随机动态性.

References)

[1]Jackman C H，Marsh D R，Vitt F M.Northern Hemisphere atmospheric influence of the solar proton events and ground level enhancement in January 2005[J].Atmospheric Chemistry and Physics，2011，11(13):6153 －6166

[2]Veselovskii I S，Yakovchuk O S.On forecasting solar proton events using a ground-based neutron monitor[J].Solar System Research，2011，45(4):354 －364

[3]Verma V K.Relationship of great soft X-ray flares with other solar activity phenomena[J].Astrophysics and Space Science，2011，334(1):83 －102

[4]薛炳森，叶宗海.太阳质子事件长期预测方法研究[J].载人航天，2007(4):47－53

Xue Bingsen，Ye Zonghai.Solar proton events forecast method research for a long time[J].Manned Space Flight，2007(4):47 －53(in Chinese)

[5]Hironori S.Solar proton event and proton propagation in the earth’s magnetosphere[J].Journal of the National Institute of Information and Communications Technology，2009，56(4):191－198

[6]Belov A.Properties of solar X-ray flares and proton event forecasting[J].Advances in Space Research，2009，43(4):467 －473

[7]Li R，Cui Y M，He H，et al.Application of support vector machine combined with K-nearest neighbors in solar flare and solar proton events forecasting[J].Advances in Space Research，2008，42(9):1469 －1474

[8]Yoichi K，Tateo G.A new modeling method of solar energetic proton events for ISO specification[J].Advances in Space Research，2008，42(7):1293 －1299

[9]Belov A，Garcia H，Kurt V，et al.Proton events and X-ray flares in the last three solar cycles[J].Cosmic Research，2005，43(3):165－178

[10]King J H.Solar proton fluences for 1977-1983 space missions[J].Journal of Spacecraft and Rockets，1974，11(6):401 －409

[11]Feynman J，Armstrong T P，Dao-Gibner L，et al.New interplanetary proton fluence model[J].Journal of Spacecraft and Rockets，1990，27(4):403 － 410

[12]Feynman J，Spitale G，Wang J，et al.Interplanetary proton fluence model:JPL 1991[J].Journal of Geophysical Research:Space Physics(1978—2012)，1993，98(A8):13281 －13294

[13]Xapsos M A，Summers G P，Shapiro P，et al.New techniques for predicting solar proto fluences for radiation effects applications[J].IEEE Trans on Nucl Science，1996，43(6):2772 －2777

[14]Xapsos M A，Summers G P，Burke E A.Extreme value analysis of solar energetic proton peak fluxes[J].Solar Physics，1998，183(1):157－164

[15]Xapsos M A，Summers G P，Barth J L，et al.Probability model for cumulative solar proton event fluences[J].Nuclear Science，IEEE Transactions on，2000，47(3):486 －490

[16]刘思峰，党耀国，方志耕，等.灰色系统理论及其应用[M].北京:科学出版社，2010

Liu Sifeng，Dang Yaoguo，Fang Zhigeng，et al.The grey system theory and its application[M].Beijing:Science Press，2010(in Chinese)

[17]李婷婷.太阳质子事件长期预测模型研究[D].北京:中国科学院，2009

Li Tingting.Solar proton events forecast model research for a long time[D].Beijing:Chinese Academy of Sciences，2009(in Chinese)