基于过程质量数据的制造系统可靠性建模分析

何益海 沈 珍 尹 超

(北京航空航天大学 可靠性与系统工程学院，北京100191)

制造系统可靠性是保障产品质量和生产效率的重要基础.已有对制造系统可靠性的衡量大多采用系统运行中产生的故障数据，而现代制造系统装备自动化程度高，系统故障率低，常规有效的故障数据非常少.与此相反，制造系统只要运行，就存在质量检验和组件退化等表征制造过程质量的数据，上述过程质量数据在生产中容易获取，更能体现制造系统的运行状态和可靠程度.而传统制造系统可靠性分析忽视了这些宝贵的数据，导致很多系统故障无法及时诊断和预测，不能很好地保证制造产品的质量与可靠性.

随着制造过程质量控制与可靠性分析技术的发展，如何有效地利用制造过程中产品质量与组件可靠性信息，充分利用过程质量数据更加准确地评价制造系统可靠性，为进一步提高产品可靠性提供可能的技术途径，已经成为该领域的热点和难点[1].对制造系统可靠性评价最常用的有效方法是故障树分析[2]，但其存在很多局限性，如没有考虑子系统之间的耦合关系、运作时间先后顺序等问题.为提高统计质量过程控制的准确性和可靠性，刘明周等人研究了产品质量统计过程中的制造质量数据的管理方法[3]，唐晓青等人提出了面向产品生命周期的多层次质量数据模型，保证了产品质量信息的纵向可追溯性以及产品改进的持续性[4].Jin等人提出了质量与可靠性交互效应 (QR-Co-Effect，Quality and Reliability Co-Effect)模型，定性地描述了制造系统组件可靠性与产品/零件质量的交互影响关系[5].结合状态空间模型研究，Chen和Jin提出QR链(Quality Reliability Chain，质量可靠性链)来对系统组件可靠性与产品质量的交互影响在多工位间的传递进行了研究[6].Zhang等人利用了制造过程中的产品尺寸信息对制造过程的稳定性进行了分析[7].孙继文等人研究了多工位制造系统中关键产品特征测量偏差与制造系统要素故障、性能衰退的交叉作用，建立了质量可靠性集成模型[8].付桂翠等人提出了基于产品可靠性的工艺系统可靠性模型[9].Li等人提出了基于制造系统运行和维护数据估计制造系统可靠性，为开展制造系统预防性维修提供依据[10].Abhulimen等人利用Markov模型法提出复杂制造系统可靠性建模分析法[11].Lin等人基于限量制造网络模型和随机任务流网络技术，利用故障和返工等运行数据建立制造系统可靠性分析模型[12－14].上述研究模型大多停留在原理分析层面，且没有更好地体现过程质量数据尤其是质量检验数据在制造系统可靠性分析中的重要作用，这不利于制造过程中对产品质量和可靠性的持续提高.

因此，本文将综合利用质量检验数据和制造系统组件的退化数据对制造系统可靠性进行建模分析.首先分析了制造系统可靠性的新内涵以及影响制造系统可靠性的因素之间的关系;然后根据质量检验数据提出了产品合格概率来表示产品质量，结合由退化数据得到的子系统失效率，建立了基于制造过程质量数据的制造系统可靠性模型.最后通过某盖板的加工系统的可靠性建模分析验证了该模型的有效性.

1 制造系统可靠性建模基础

1.1 制造系统可靠性

制造系统是制造过程及其所涉及的硬件、软件和人员所组成的一个将制造资源转变为产品或半成品的输入/输出系统，其中硬件包括生产设备、工具、刀具等.制造系统可靠性通常定义为一个制造系统在操作条件和规定时间下完成预期功能的能力.

传统的制造系统可靠性的量化一般是用制造系统在操作条件下的正常运行时间即平均无故障时间(MTBF，Mean Time Between Failure)来衡量系统可靠性的好坏，没有考虑产品质量.而从制造系统的定义中可以看出，制造系统不仅包括设备和刀具等组件的正常运行，还包括完成预期功能即产出的产品或半成品.实际生产中希望一个可靠性高的制造系统，不仅正常运行的时间长，同时产出的产品质量和可靠性也高.

因此本文在考虑产品质量的基础上分析制造系统可靠性，并定义制造系统可靠度R(k)是在一段时间内，系统组件没有发生失效且生产出的产品是合格品的概率，可用下式表达:

在制造系统中，当前工位的输出产品质量依赖于当前工位系统组件可靠性以及由前道工位输入的产品质量，以及当前工位的制造系统组件可靠性受当前工位输入产品质量的影响.产品质量与制造系统组件可靠性在制造过程中有交互作用，如图1所示.

图1 产品质量与制造系统组件可靠性交互作用Fig.1 Co-effect of product quality and component reliability of manufacturing systems

产品质量在一定程度上反映了制造系统的可靠性，在本文对制造系统可靠性的分析中，考虑产品质量特征对制造系统组件可靠性的影响以及组件可靠性对系统可靠性的影响，以保障产品质量和可靠性为目的来分析制造系统可靠性.

1.2 产品合格概率

当所有零件都合格，装配出的产品质量却不合格，这在生产中很常见.这是由于合格零件的尺寸偏差在允许的范围内，才判定其合格，但是这些尺寸偏差在装配的时候会累积传递，最后造成产品的偏差过大，质量不合格.本文提出产品合格概率来表示产品质量，与通常所指的合格率不同.合格率指在产品检测中，合格品数占产品总数的百分比，而本文产品合格概率表示产品合格的程度.

产品在第k工位上的质量用X(k)表示，则X(k)=[X1(k)，X2(k)，…，Xn(k)].其中 Xi(k)是指零件上的第 i个质量特性(i=1，2，…，n).由状态空间方程及偏差流理论可得

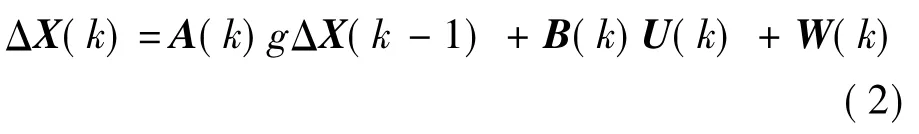
式中，ΔX(k)表示第k工位上的产品尺寸偏差;A(k)，B(k)，U(k)分别表示制造系统参数矩阵;W(k)表示残差;A(k)·ΔX(k－1)表示关键产品质量特性的一部分;B(k)U(k)表示关键控制特性的一部分.

以夹具系统为例，用L(k)表示夹具系统参数，T(k)表示零件尺寸的公差.产品公差是产品的质量特征之一，它反映了产品的质量和级别.

式中，f(L(k))表示制造系统生产的产品质量;ΔX(k)仅考虑了夹具参数的误差，并未将机加工特征的误差和过程控制的误差考虑进去.

f(L(k))是非线性的，是 X=(X1，X2，…，Xn)的非线性函数，采用Taylor展开可将其线性化.

假设

其中 μx=(μx1，μx2，…，μxn)，是 f(x)的均值点.则均值 μf=f(μx1，μx2，…，μxn)，标准差.

则产品合格的概率可用下式表达:

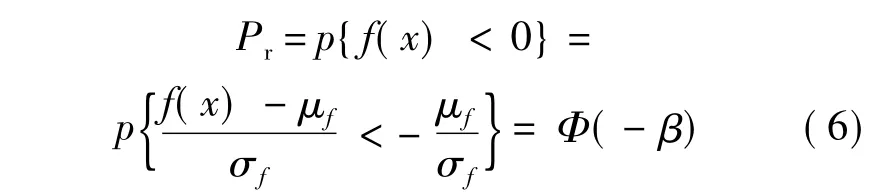
1.3 制造系统组件退化失效率

制造系统由于组件导致的可靠性降低主要是组件发生故障和组件退化磨损.由于制造系统只要运行，就一定存在刀具磨损、退化等信息，但不一定有故障数据.结合引言中对这两部分数据的分析，本文将在分析组件可靠性对制造系统可靠性影响时仅考虑磨损退化信息.

为简化问题，假设多工位制造系统中所有的组件都是连续的，各个工位上均是单个组件工作，并且各组件之间发生故障是相互独立的，即系统可靠性模型是一个串联模型[15].

制造系统中组件的累计损耗随着工序数量的增加而增加，用Δ(k)表示单个工位的磨损量，则k个工序后组件的累积磨损量Z(k)=Z(k－1)+Δ(k).若所有磨损退化过程符合独立同分布(大部分机械产品)，则

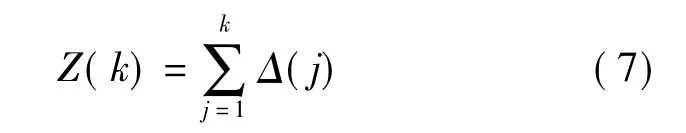
由中心极限定理，Z(k)可近似于正态分布N(k·E[Δ(j)]，k·Var[Δ(j)]).

如果制造系统的组件在t时刻都未发生故障，在工位k可工作的系统组件在工位k+1发生故障的概率可表示为λk(t).假设单个组件的失效服从指数分布(对于高可靠性的复杂系统，指数分布可近似地作为其组件失效分布模型)，则在工位k上组件可靠性可用式(8)表达(不计组件磨损对组件强度的影响，所以故障率λk(t)可视为恒定):

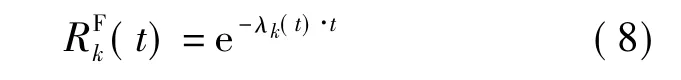
输入产品的质量存在偏差，其会导致加工组件的损耗加速，故有

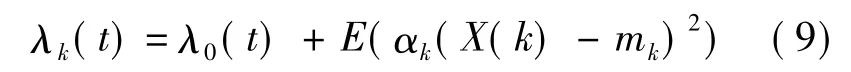
其中，λ0(t)为不考虑输入产品质量对组件影响的失效率(初始故障率);X(k)为产品在第k工位上的质量的测量值;mk为输入产品质量的标准值;αk为修正系数，体现了输入产品质量的偏差对组件的磨损影响.

则在整个系统的可靠性为

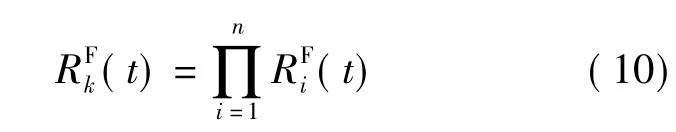
2 制造系统可靠性建模

2.1 模型描述及建模步骤

如图1所示，在制造过程中，对产品关键质量特性的测量能反映出产品质量偏差的传递，根据偏差传递模型可得出产品质量;单个组件的工位连续形成串联系统，可得到子系统的可靠性;最后由产品质量和制造系统组件的可靠性综合反映出制造系统可靠性.建模步骤如下:

1)首先明确研究对象以及目的;

2)确定产品的关键质量特性参数，并收集相关的原始数据;

3)根据原始数据，建立组件可靠性对制造系统可靠性的影响模型，求得第k工位上组件磨损Z(k)以及组件故障率λk(t);

4)建立产品质量对制造系统可靠性影响的模型，求得Pr;

5)综合3)和4)两步的结果，建立面向过程质量数据的制造系统可靠性模型，得出R(t).

2.2 数学模型

根据第1.1节中制造系统可靠性的定义:

首先计算Rf(t)，其表示制造系统在t时间内没有发生失效的概率.考虑到组件磨损退化对组件发生故障的影响，η为允许的最大退化量.

将以上模型进行综合，其中Rq(t)表示产品合格的概率，则制造系统可靠性的最终数学模型如式(12)所示.

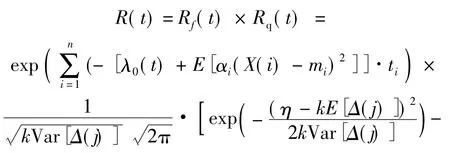
3 案例研究

3.1 案例背景

某铸锻厂根据其产品盖板的加工工艺文件设计一条生产线，投入生产后根据收集到的系统故障，得到其系统可靠性较好，但是检验的产品合格率不是很高.该厂通过更换磨损刀具，定期维修来保证系统可靠性维持在较高水平，以此来减少不合格产品，但是收效甚微.由此可见制造系统较高的可靠性不能保证产品有较高的合格品率，以该盖板加工过程为例，对本文提出的面向过程质量数据的制造系统可靠性模型进行分析和验证.盖板的零件特征和加工过程见图2、表1和表2.

图2 盖板加工尺寸图(单位:mm)Fig.2 Dimensions of cover plate machining

表1 零件特征及加工过程Table 1 Features and processes of the part

表2 零件参数Table 2 Part parameters

3.2 建模与求解

加工过程中夹具和刀具的参数参考文献[16]，结合偏差流模型，将原始数据代入到式(2)中，产品尺寸输出结果如表3第3列所示.

表3 各工位加工时间及故障率Table 3 Failure rate and working time of each process

求解步骤如下:

1)首先制造系统组件衰退和初始故障率等相关参数可由历史数据得:

初始故障率 λ0(t)=λ0=4 ×10－6，修正系数αk=0.001，由式(9)计算可得每个工位的故障率，见表3的最后一列.

2)计算Pr，即求β值.

零件的4个关键尺寸的公差分别为0.2，0.021，0.2，0.2 mm.求解过程相同，可以同时求解.将表1与表2中的数据代入式(2)中，经过Taylor展开，因假设原始数据是服从正态分布的，故

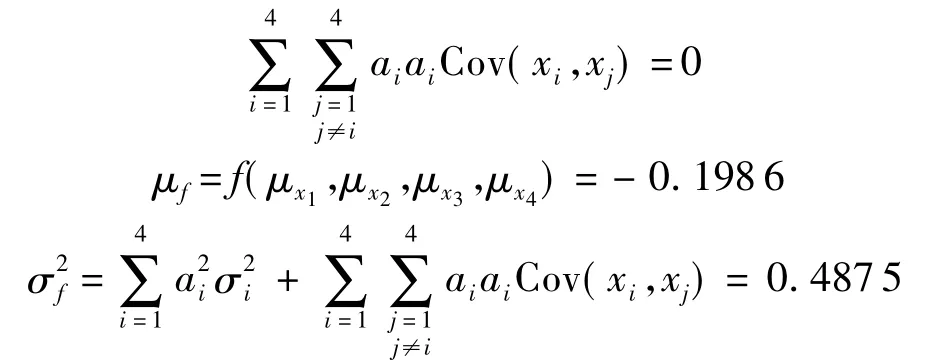
将上述相关数据代入式(12)可求得R(t).

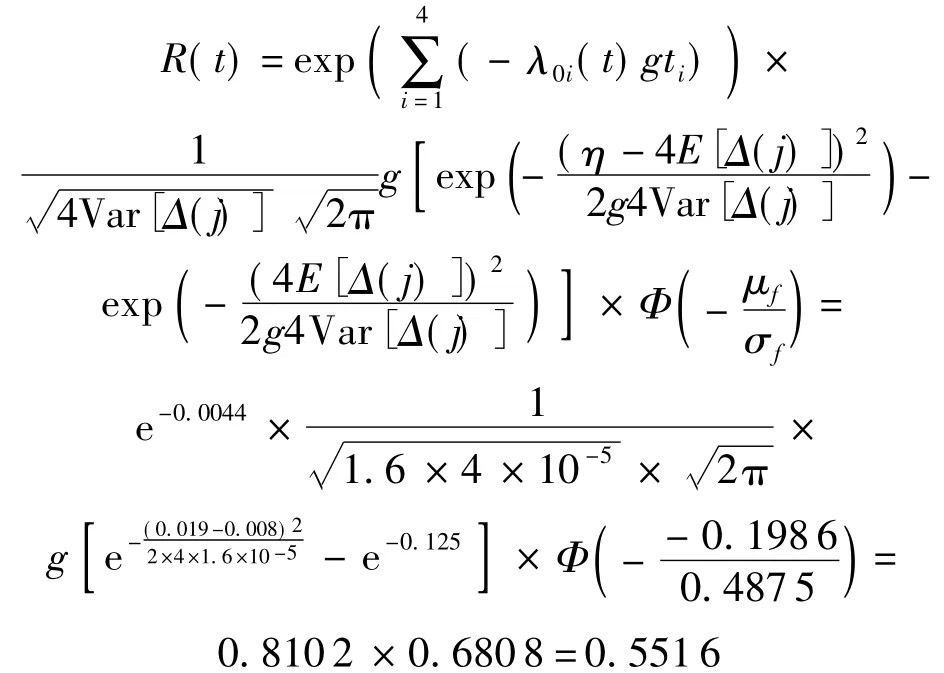
3.3 结果分析

根据实际入厂调研和反馈，发现该盖板加工系统是新建的，正处于磨合期，盖板的合格品率不高.根据原始数据，当仅仅考虑系统组件退化磨损和故障失效时，制造系统可靠性约为0.8.但是将该系统生产的产品合格情况考虑进去，则大大降低了系统可靠性，仅为0.55.计算结果反映了该新建的制造系统实际生产能力达不到预期水平，对系统可靠性预计过高了.

这一结果符合实际情况，当制造系统的状态与生产某一产品所需要的系统状态偏离过大，将会造成实际制造水平远远低于预计值.

4 结论

本文对制造系统可靠性的内涵作了新的诠释，并在分析制造系统可靠性的过程中，将产品质量作为一个重要因素加入进行考虑，在深入分析产品质量与组件可靠性的交互影响的基础上，建立了基于过程质量数据的制造系统可靠性模型.采用制造过程中的产品合格概率和组件可靠性作为变量，相对于已有研究不仅具有数据实时性和准确性，更加便于数据的收集和计算.最后通过案例应用对该模型进行了验证.研究结果表明:

1)制造系统可靠性建模时需要重视制造过程质量数据.模型的结果反映出若不考虑产品质量、组件退化和故障的交互作用，系统可靠性将会被过高地估计.

2)过程质量数据能够为制造系统开展预防性维修提供实时数据支撑.模型的结果还反映出制造系统可靠性与产品质量水平存在关联关系，过程质量水平的变化在一定程度上反映出制造系统可靠性的变化规律，这为进一步研究质量驱动的制造系统可靠性保障技术提供了方向，也为后续深入研究制造阶段产品可靠性退化机理和抑制技术提供了参考.

References)

[1]Inman R R，Blumenfeld D E，Huang N J.Survey of recent advances on the interface between production system design and quality[J].Institute of Industrial Engineers，2013，45(6):557－574

[2]Dutuit Y，Rauzy A.Approximate estimation of system reliability via fault tree[J].Reliability Engineering and System Safety，2005，87(2):163 －172

[3]刘明周，任兰，张铭鑫.产品质量统计过程中的制造质量数据管理方法研究[J].计算机集成制造系统，2005，11(2):280－283

Liu Mingzhou，Ren Lan，Zhang Mingxin.Research on manufacturing quality data management methods of quality statistical process control[J].Computer Integrated Manufacturing Systems，2005，11(2):280 －283(in Chinese)

[4]唐晓青，胡云，王雪聪.面向产品生命周期的质量数据模型[J].北京航空航天大学学报，2006，32(10):1135 －1140

Tang Xiaoqing，Hu Yun，Wang Xuecong.Quality data model in product lifecycle[J].Journal of Beijing University of Aeronautics and Astronautics，2006，32(10):1135 －1140(in Chinese)

[5]Jin J，Chen Y.Quality and reliability information integration for design evaluation of fixture system reliability[J].Quality and Reliability International，2001，17(5):355 － 372

[6]Chen Y，Jin J H.Quality-reliability chain modeling for system-reliability analysis of complex manufacturing process[J].IEEE Transactions on Reliability，2005，54(3):475 －488

[7]Zhang F P，Liu J P，Yan Y，et al.Dimensional quality oriented reliability modeling for complex manufacturing process[J].International Journal of Computational Intelligence Systems，2011，4(6):1262－1268

[8]孙继文，奚立峰，潘尔顺，等.面向产品尺寸质量的制造系统可靠性建模与分析[J].上海交通大学学报，2008，42(7):1100－1104

Sun Jiwen，Xi Lifeng，Pan Ershun，et al.Product dimensional quality oriented reliability modeling and analysisof manufauring system[J].Journal of Shanghai Jiaotong University，2008，42(7):1100－1104(in Chinese)

[9]付桂翠，上官云，史兴宽，等.基于产品可靠性的工艺系统可靠性模型[J].北京航空航天大学学报，2009，35(1):9 －12

Fu Guicui，Shangguan Yun，Shi Xingkuan，et al.Processing system reliability model based on products reliability[J].Journal of Beijing UniversityofAeronauticsand Astronautics，2009，35(1):9－12(in Chinese)

[10]Li L，Ni J.Reliability estimation based on operational data of manufacturing systems[J].Quality and Reliability Engineering International，2008，24(7):843 － 854

[11]Abhulimen K E.Model for risk and reliability analysis of complex production systems:application to FPSO/flow-Riser system[J].Computers and Chemical Engineering，2009，33(7):1306－1321

[12]Lin Y K，Chang P C.System reliability of a manufacturing network with reworking action and different failure rates[J].International Journal of Production Research，2012，50(23):6930 －6944

[13]Lin Y K，Huang C F，Chang P C.System reliability evaluation of a touch panel manufacturing system with defect rate and reworking[J].Reliability Engineering and System Safety，2013，118:51－60

[14]Lin Y K，Chang P C.A novel reliability evaluation technique for stochastic-flow manufacturing networks with multiple production lines[J].IEEE Transactions on Reliability，2013，62(1):92－104

[15]曾声奎，冯强.可靠性设计与分析[M].北京:国防工业出版社，2011:64－112

Zeng Shengkui，Feng Qiang.Reliability design and analysis[M].Beijing:National Defense Industry Press，2011:64 －112(in Chinese)

[16]Shi J.Stream of variation modeling and analysis for multistage manufacturing processes[M].Boca Raton，FL:CRC Press，2007:155－180