固体运载器飞行动力学逆问题分类
李世鹏 梁欣欣 荣晶晶 张 艳
(北京宇航系统工程研究所,北京100076)
在固体运载器飞行力学研究领域通常会遇到诸如需用推力设计、需用控制力分析、误差分离、多相绕流场下的运载器受力分析等问题,这些与已知运载器受力求解运动的问题有所不同.以上问题可以归纳为已知运载器的真实运动参数或运动期望,来确定运载器受力和力矩或状态参数,即所谓飞行动力学逆问题.固体运载器飞行动力学逆问题通常涉及到固体火箭发动机、空气动力学、弹道、制导和控制等多个学科,研究的成果多集中在具体问题本身,目前还未有对这些问题系统的开展分类研究的报道.在其他飞行器,如飞机飞行动力学逆问题等研究领域,多以飞行试验数据辨识气动参数和求解操纵规律[1-7]等具体研究内容为多.文献[8]系统性地对逆问题进行了研究,但内容侧重有限自由度动力系统动力学逆问题,对飞行器研究对象内容阐述较少.对固体运载器飞行动力学逆问题进行分类研究,有助于推动逆问题研究领域的发展,从而更好地开展飞行动力学逆问题研究.文中对固体运载器的飞行动力学逆问题进行了总结归纳,在此基础上将逆问题划分为3类,即需用力计算、外力辨识和参数辨识.针对每类问题建立了统一的数学描述,探讨了基本求解方法并给出了相应的典型应用.本文研究结果对新的复杂动力学逆问题的分析求解具有一定的指导意义.
1 动力学逆问题分类及基本解法
1.1 第一类逆问题——需用力计算
涉及固体运载器需用力计算的飞行动力学逆问题可统一表达为

式中,Em为运载器期望的运动状态;Cm为施加力和力矩作用前的运动状态;m为运载器质量;J为运载器的转动惯量;Jk为运载器的惯性积;Freq和Mreq分别为使运动状态由Cm转换至Em所需的外力和外力矩.
由式(1)表征的固体运载器飞行动力学逆问题常见如下:
1)给定固体运载器的最大射程期望Lmax,求运载器在飞行过程中的需用推力;
2)在规定的时间t内,要求运载器俯仰姿态角由φc变化到φr,求所需的调姿力矩等.
1.2 第二类逆问题——外力辨识
涉及固体运载器外力辨识的飞行动力学逆问题可统一表达为
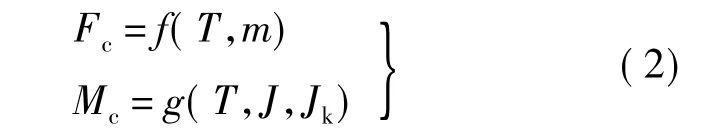
式中,T为试验测量得到的运载器运动参数,如过载系数、速度、加速度、角速度和角加速度等;Fc为对应飞行状态下运载器所受外力;Mc为对应飞行状态下运载器所受外力矩.
由式(2)表征的固体运载器飞行动力学逆问题常见的如下:
1)固体运载器水下弹射缩比试验中,基于测量得到的运动参数,计算固体运载器水下运动过程中受到的合外力和合外力距;
2)遥测飞行试验中,基于遥测得到的运动参数计算气动力或发动机推力.
1.3 第三类逆问题——参数辨识
涉及固体运载器参数辨识的飞行动力学逆问题可统一表达为
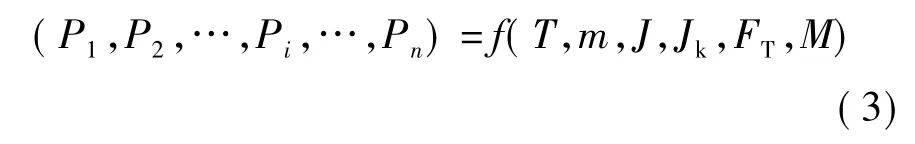
式中,FT和M分别为依据试验测量信息计算得到的外力和外力矩;Pi(i=1,2,…,n)为待辨识的参数.
由式(3)表征的固体运载器飞行动力学逆问题常见的如风场参数辨识和误差系数分离等.
1.4 基本解法
根据所研究问题的不同,逆问题求解的方法也有所不同.如果式(1)~式(3)表征的动力学逆问题可以推导得到显示表达式,则从方程中可直接得到解析解.解析法通常是先通过将固体运载器刚体运动方程变换,再通过多项式变换将待求解参数转换到等式的左边,等式右边则以一系列已知的参数表达,则通过求解变换后的方程可解析得到待求解参数.式(4)给出了固体运载器质心加速度求解方程:
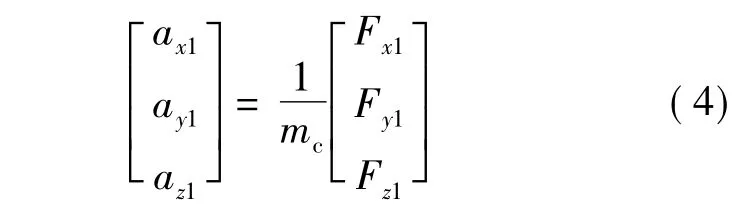
式中,ax1,ay1,az1分别为固体运载器在箭体系的加速度;mc为固体运载器质量;Fx1,Fy1,Fz1分别为固体运载器合外力在箭体系各轴上的投影;在正问题研究中,已知 mc,Fx1,Fy1,Fz1可求解得到加速度值.若在试验中通过惯性器件测量得到了ax1,ay1,az1,要分析运载器受力情况,则可将式(4)变换,如下:
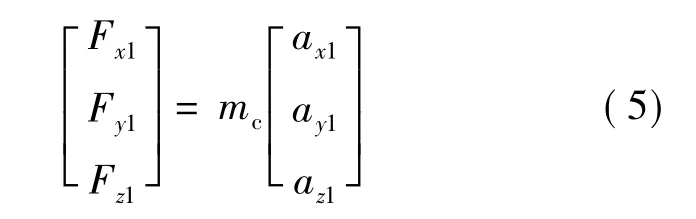
由式(5)可以得到逆问题的解.在运动方程涉及的参数较多时,为了能够解析求解,要假定一些参数固定,所以解析法通常适用于快速估算求解或计算精度要求不高的情况.
如果式(1)~式(3)表征的动力学逆问题无法通过公式显示表达,可将待求解参数作为设计变量,建立目标函数,同时考虑设计约束,建立优化模型,如下:
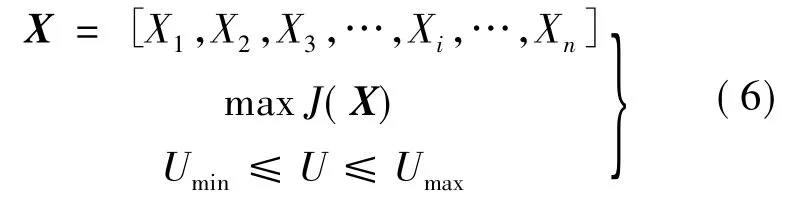
式中,X为设计变量;J(X)为目标函数;U为约束条件.
运用优化算法对式(6)求解,可得到逆问题的解,这一过程中往往伴随有正问题求解的环节.
2 典型飞行动力学逆问题举例
2.1 第一类逆问题——主发动机需用推力设计
对于多级固体运载器来说,在质量一定的前提下,其运载能力主要取决于各级发动机的推力曲线,有关的弹道模型见文献[9-10],有关的优化求解方法参见文献[11-14].在保持发动机装药量、总冲、工作时间不变的情况下,构造各种基本线型的内弹道推力曲线,如图1所示.通过确定对运载器运载能力等有利的需用推力曲线,来使得运载能力最大化,属于典型的第一类逆问题.
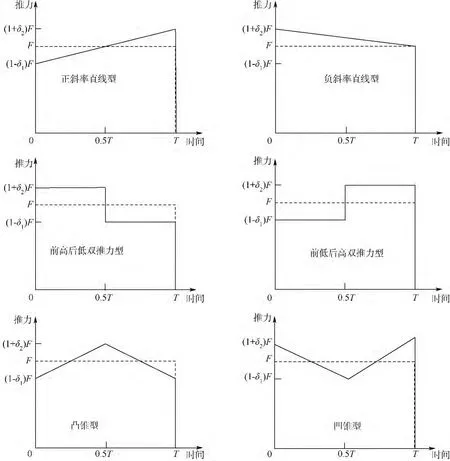
图1 推力基本线型Fig.1 Curves of engine thrust
在运载器运动模型基础上,假定二级以上采用平均推力曲线,建立一级需用推力曲线优化模型,运用自适应差分进化算法优化得到的最优需用推力曲线见图2.
优化结果表明,与平均推力曲线形式相比,优化得到的需用推力曲线可使运载器运载能力增加2%以上.
2.2 第二类逆问题——合外力辨识
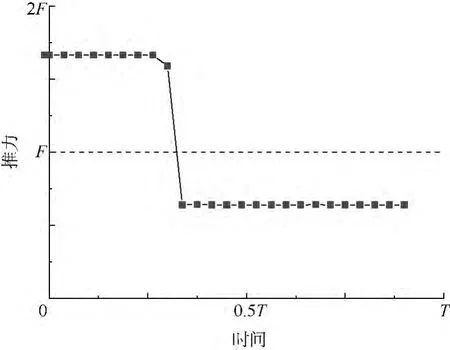
图2 最优需用推力曲线Fig.2 Optimal required thrust curve
对于水下发射的固体运载器来说,由于在出筒、水中和出水运动过程中经历了围绕本体的空化流动,并且运载器水中绕流具有高动压、非定常及多相介质的特点,致使运载器的水动力的描述十分困难.不仅如此,在水中运动时,推动运载器出筒的发射气体也对运载器在水中的受力状态有一定影响.同时,运载器在运动过程中还受到洋流、波浪等随机因素的干扰.这些复杂的物理现象交织在一起,非常难以综合分析清楚运载器的受力情况.惯性平台、过载传感器等测量设备可以通过测量得到运载器出筒、水中和出水运动过程中的加速度和过载,这些运动参数都体现了运载器受力情况.应用惯性测量设备测量得到的参数来计算合外力的问题,即合外力辨识问题属于典型的第二类飞行动力学逆问题.根据文献[9-10]运载器动力学模型,按照1.4节的基本解法,可得到合外力辨识模型.
图3给出了某飞行试验运载器水中和出水运动过程中的法向合外力辨识结果与水动压力积分结果的对比曲线.图3可见,两条曲线变化规律基本一致,最大最小峰值点基本重合,两者之间的差异是由于表面压力传感器测点有限,积分时采用了假设条件而引入的.
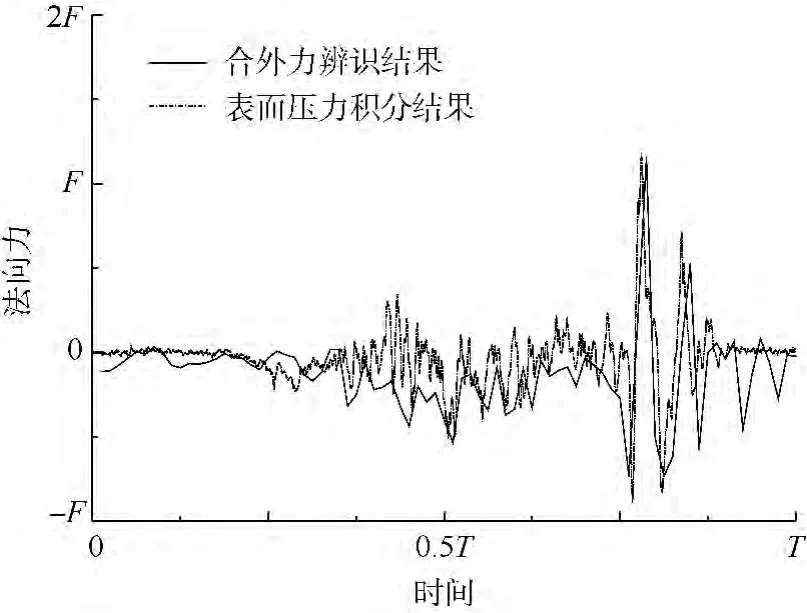
图3 合外力辨识结果与压力积分结果对比曲线Fig.3 External force by identification and the integration of pressure
2.3 第三类逆问题——误差分离
固体运载器飞行过程中存在着方法误差、惯性器件工具误差等多种误差,对运载器落点精度有直接影响.飞行试验过程中通过遥外测手段可以获得运载器的遥测和外测运动参数,依据这些运动参数对误差进行分离,可获得影响落点精度的各类误差值,误差分离有关的模型和方法见文献[15].误差分离的结果是对制导系统工作情况进行评价的重要依据,可用于分析惯性器件工作状态,同时也是精度鉴定所需重要数据源之一.固体运载器误差分离问题属于典型的第三类飞行动力学逆问题.根据文献[15]误差分离有关的模型和方法,按照1.4节基本解法,可建立对应的优化模型,运用优化算法可得到误差分离结果.
图4给出了利用工具误差分离结果计算得到的惯性系3方向视速度差与飞行试验得到的视速度差对比曲线,图中均对视速度差和时间进行了归一化处理.可以看出两者一致性较好.
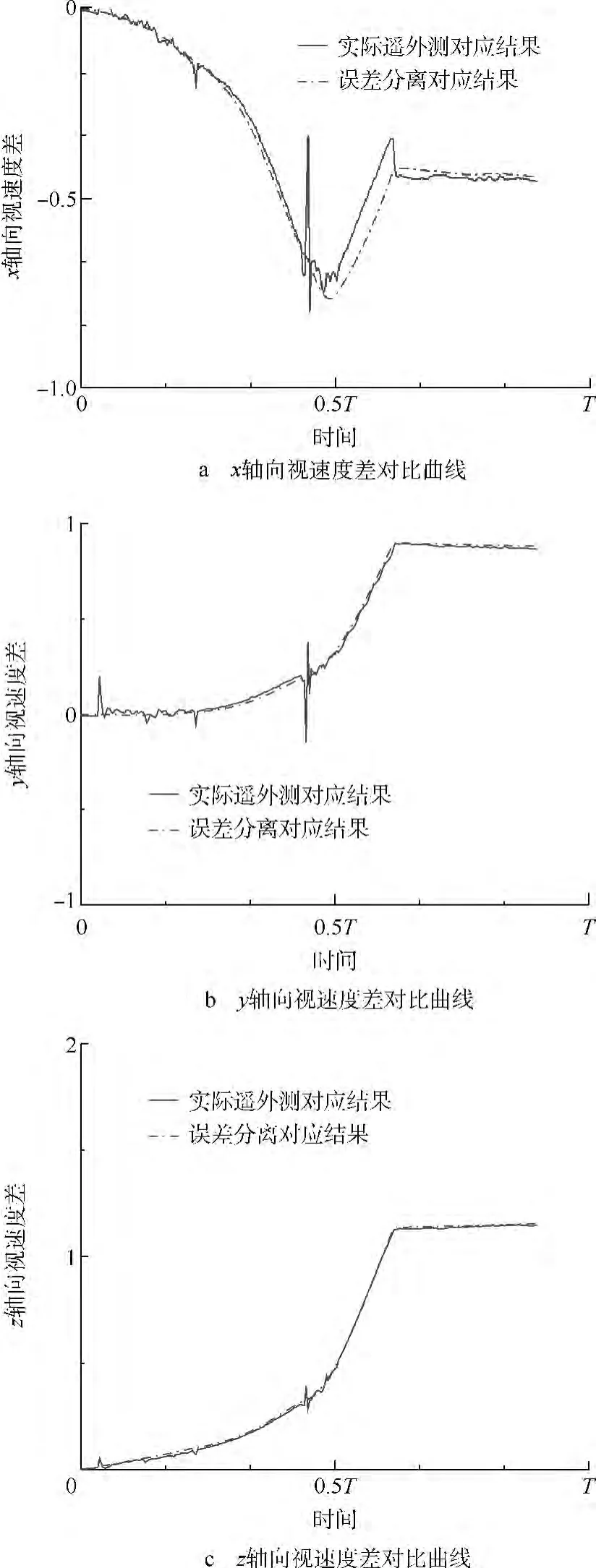
图4 发射惯性系视速度差对比曲线Fig.4 Apparent velocity difference by error separation and the difference by ballistic measurement
3 结论
1)固体运载器飞行动力学逆问题可归纳为需用力计算、外力辨识和参数辨识3类,基本解法归纳概括为解析求解法和优化求解法2种.解析求解法通常要引入简化假设,在简化的模型上得到问题的解,因而解的精度不高;优化求解法适用于复杂模型,可以得到较高精度的解,但由于需要大量的复杂数学运算,计算周期较长.
2)对应3类逆问题,给出了主发动机需用推力设计、水中运动过程中的合外力辨识和误差分离3个典型工程应用.优化后的主发动机需用推力曲线可以得到更大的运载能力,主要原因是在优化的推力曲线下,运载器飞行过程中气动阻力损失最小;合外力辨识的结果与压力积分结果变化规律基本一致,差异主要是测压点有限,在压力积分时引入的简化假设引起;误差分离结果与试验测量结果一致性较好,部分差异主要由误差分离模型的精度和飞行试验测量精度引起.3个典型工程问题求解过程及结果表明了固体运载器飞行动力学逆问题分类和基本解法的合理性.
References)
[1]Rohlf D,Schmidt S,Irving J.Stability and control analysis for an unmanned aircraft configuration using system-identification techniques[J].Journal of Aircraft,2012,49(6):1597 - 1609
[2]Hamel P G,Jategaonkar R V.Evolution of flight vehicle system identification[J].Journal of Aircraft,1996,33(1):9 - 28
[3]杨超.直升机飞行动力学逆问题研究综述[J].飞行力学,2000,18(2):5 -8
Yang Chao.Summary about inverse problem of helicopter flight dynamics[J].Flight Dynamics,2000,18(2):5 - 8(in Chinese)
[4]Malone J B,Vadyak J,Sankar L N.Inverse aerodynamic design method for aircraft components[J].Journal of Aircraft,1987,24(1):8-9
[5]Ata A A.Inverse dynamic analysis and trajetory planning for flexible manipulator[J].Inverse Problems in Science and Engineering,2010,18(4):549 -566
[6]Mira-Cristiana A.The energy-free equations of the 3D inverse problem of dynamics[J].Inverse Problems in Science and Engineering,2005,13(5):545 -558
[7]杨超,熊良玉,张晓谷.直升机机动飞行逆仿真研究[J].北京航空航天大学学报,2000,26(6):697-700
Yang Chao,Xiong Liangyu,Zhang Xiaogu.Inverse simulation for helicopter maneuvering flight[J].Journal of Beijing University of Aeronautics and Astronautics,2000,26(6):697 - 700(in Chinese)
[8]梅凤翔.动力学逆问题[J].北京:国防工业出版社,2009
Mei Fengxiang.Inverse problem of dynamics[M].Beijing:National Defence Industrial Press,2009(in Chinese)
[9]龙乐豪.总体设计(I)[M].北京:中国宇航出版社,1993
Long Lehao.System design(I)[M].Beijing:China Astronautic Publishing House,1993(in Chinese)
[10]贾沛然,陈克俊,何力.远程火箭弹道学[M].长沙:国防科技大学出版社,1993
Jia Peiran,Chen Kejun,He Li.Long-range rocket ballistics[M].Changsha:National University of Defence Technology Press,1993(in Chinese)
[11]梁欣欣,辛万青,张耐民,等.基于组合算法的多级固体运载火箭运载能力优化[J].导弹与航天运载技术,2011(5):6-10
Liang Xinin,Xin Wanqing,Zhang Naimin,et al.Launch capability optimization for multi-stage solid launch vehicle using a hybrid optimization method[J].Missiles and Space Vehicles,2011(5):6-10(in Chinese)
[12]洪蓓,梁欣欣,辛万青.固体运载火箭多约束弹道优化[J].导弹与航天运载技术,2012(3):1-5
Hong Bei,Liang Xinxin,Xin Wanqing.Multi-constraint trajectory optimization for solid launch vehicle[J].Missiles and Space Vehicles,2012(3):1 -5(in Chinese)
[13]李瑜,杨志红,崔乃刚.助推-滑翔导弹弹道优化研究[J].宇航学报,2008,29(1):66 -71
Li Yu,Yang Zhihong,Cui Naigang.A study of optimal trajectory for boost-glide missile[J].Journal of Astronautics,2008,29(1):66-71(in Chinese)
[14]刘欣,杨涛,张青斌.助推-滑翔导弹弹道优化与总体参数分析[J].弹道学报,2012,24(3):43 -48
Liu Xin,Yang Tao,Zhang Qingbin.Trajectory optimization and parameter analysis for boost-glide missile[J].Journal of Ballistics,2012,24(3):43 -48(in Chinese)
[15]龙乐豪.总体设计(II)[M].北京:中国宇航出版社,1993
Long Lehao.System design(II)[M].Beijing:China Astronautic Publishing House,1993(in Chinese)

