Partial Wave Amplitude and Coupling Constants∗

Nureli Yasin,Sayipjamal Dulat,Reyima Rashidin

(College of Physics Science and Technology,Xinjiang University,Urumqi,Xinjiang 830046,China)

Abstract: By using Effective Lagrangian method,we provide Partial Wave Amplitudes(PWA)and decay width forfive interesting exotic baryon decay channels.And,we also calculate the coupling constants for the nucleon-nucleon-meson by using the branching ratios from particle data group(PDG).

Key words:interaction vertex,matrix element,decay width,branching ratio,coupling constant

0 Introduction

To understand the internal structure of nucleon and the strong interaction in the nonperturbative QCD domain,the study of excited nucleon states is very important.In the quark model,baryon state and their excited states are complex system of quarks and gluons.Most of the spatial ground state of baryons are very successful in both experiments and theory,but have serious problems for the predictions of baryon excitation states.To understand the internal quarkgluon structure of baryons,there are various proposed configurations:(a)the classical constituent three quark(qqq)states;(b)qqqg hybrid states[2];(c)diquark-quark states[3,4];(d)meson-baryon states[5∼8];(e)pentaquark with diquark clusters[9,10],etc.In last few years,a considerable amount of precise data are observed for various excited nucleon production and decay channels.The experimental results showed thatbaryons areN∗(1535),Λ∗(1405)and Σ∗(1620)[11]with excitation energies of 596MeV,290MeV and 431MeV,respectively.These results provided a great opportunity to make quantitative investigations of the baryon structure.

To provide a consistent and complete picture of baryon resonances,the various possible decay channels need to be explored.At the same time,it is necessary to understand their structure and properties such as masses,decay widths,branching ratios,spins,parities,electromagnetic form factors,magnetic moments,polarizabilities,etc.

This paper is organized as follows.In section 1,we provide the necessary tools for the calculation of the tensor amplitudes within covariant tensor formalism.In section 2,we present covariant tensor formalism of PWA and decay widths forfive interesting decay channels.In section 3,we calculate the coupling constants for each process.

1 Formalism

In this section,we present the necessary tools for the construction of partial wave amplitudes for the following decay processes

the partial wave amplitudes Ma→b+ccan be constructed by using pure orbital angular momentum covariant tensorsprojectionoperatorsεµ(p,s),spinwavefunctionsu(p,sp),spinwavefunctionsmatrictensors gµν,totallyantisymmetricLevi-Civitatensor?µνλσandthefourmomentaofparticipatingparticles;heretheindicesµ,ν,λ and σ run from 1 to 4 over x,y,z and t.

For a given hadronic decay process a→b+c,in the L-S scheme on hadronic level,the initial state is described by its 4-momentum pµand its spin state sa;thefinal state is described by the relative orbital angular momentum state of(b+c)system Lbcand their spin states(sb,sc).The spinwavefunction is the standard Dirac spinor u(p,s)or v(p,s)and the spin 1 wave function is the standard spin 1 polarization four-vector εµ(p,s)for a particle with momentum p and spin projection s

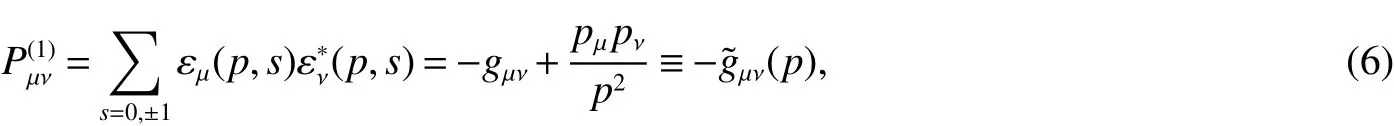
with pµεµ(p,s)=0,which states that spin-1 wave function is orthogonal to its own momentum.Here the Minkowsky metric tensor has the form

Spin wave functions for particles of higher spins are constructed from these two basic spin wave functions with C-G coefficients

for a particle with integer spin n≥2,and

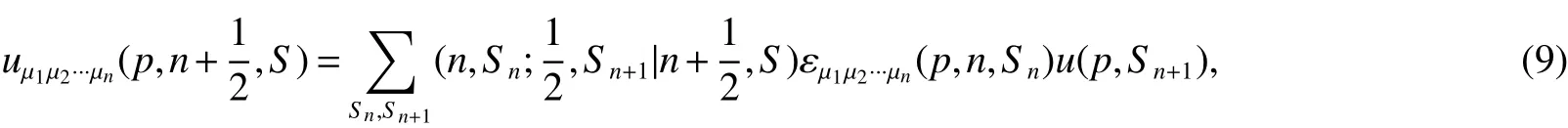
for a particle with half integer spin n+of n≥1.For an antiparticle with half integer spin n+of n≥1,one has

For a process a→b+c,if there exists a relative orbital angular momentum Lbcbetween the particle b and c,then the orbital angular momentum Lbcstate can be represented by covariant tensor wave functions

where r=pb−pcis the relative four momentum of the two decay products in the parent particle rest frame;=−r2;and

In the L-S scheme,we need to use the conservation relation of total angular momentum

Besides parity should be conserved,which means

where ηa,ηband ηcare the intrinsic parities of particles a,b and c,respectively.From this relation,one knows whether L should be even or odd.Then from Eq.(15)one canfigure out how many different L-S combinations,which determine the number of independent couplings.

Projection operator of the particle and anti-particle with spin

The partial decay rate of a particle of mass M into two particles a and b is in its rest frame is given in terms of the Lorentz-invariant matrix element M by

where dω=dφad(cosθa)is the solid angle of particle a.The decay width is

The branching fraction for a decay is the fraction of particles which decay by an individual decay mode with respect to the total number of particles which decay.If we denote the total decay width(that is,the inverse lifetime,the sum of all possible decay widths for all possiblefinal particles)as Γ(a→all),then a ”branching ratio”is defined as

2 Partial Wave Amplitudes and Decay Widths

Using the formalisms in the previous section for the decay

wefind one independent covariant amplitude

where gK∗0K+π−is coupling constant of this process;εµ(pK∗0,sK∗)is the spin 1 wave function;(pK+ − pπ−)µis the relative four-momentum of the two decay products in the parent particle rest frame.

To compute decay width,we need an expression for|M|2.Note that the square modulus of the decay amplitude,which gives the decay probability of a certain configuration should be independent of any particular frame,that is,a Lorentz scalar.Thus

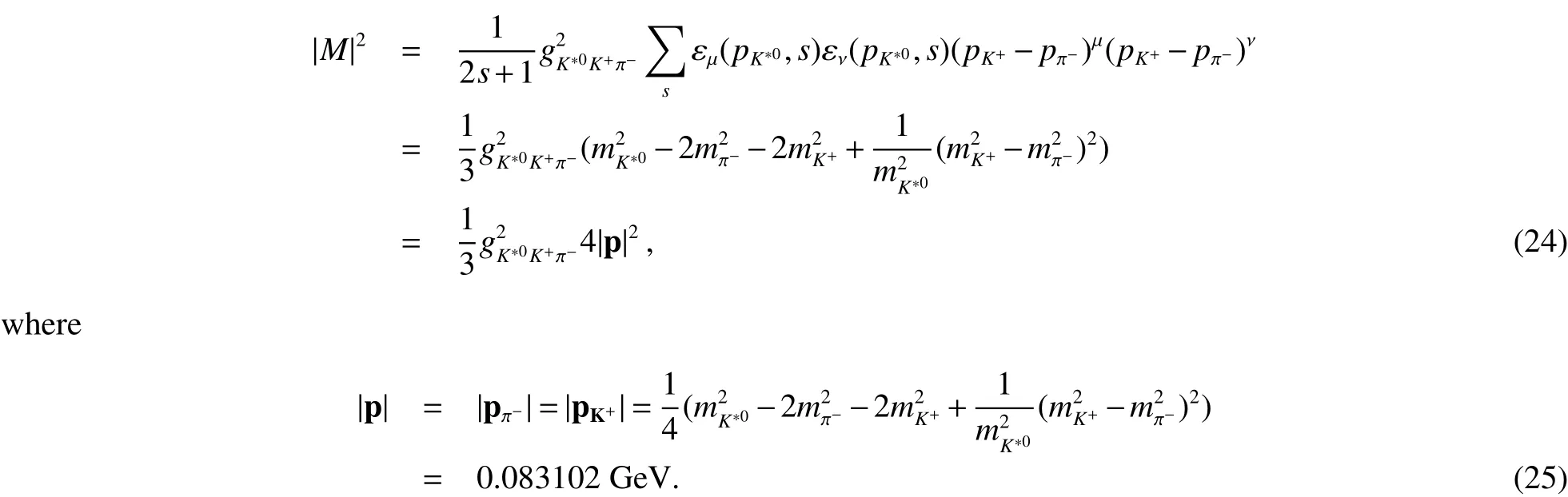
Inserting Eq.(24)into Eq.(19),we get decay width

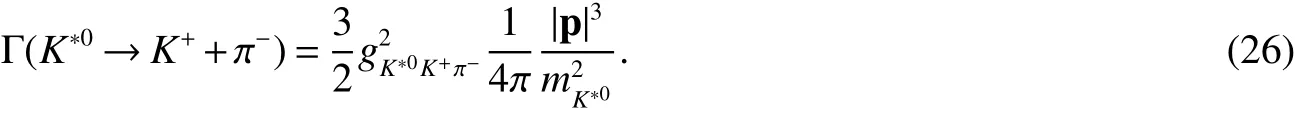
For the decay

we have the following partial wave amplitude

where gΣ∗+Λπ+is coupling constant of this processwave function of the particle;is the spinwave function;is the four momentum of the pion.And thus

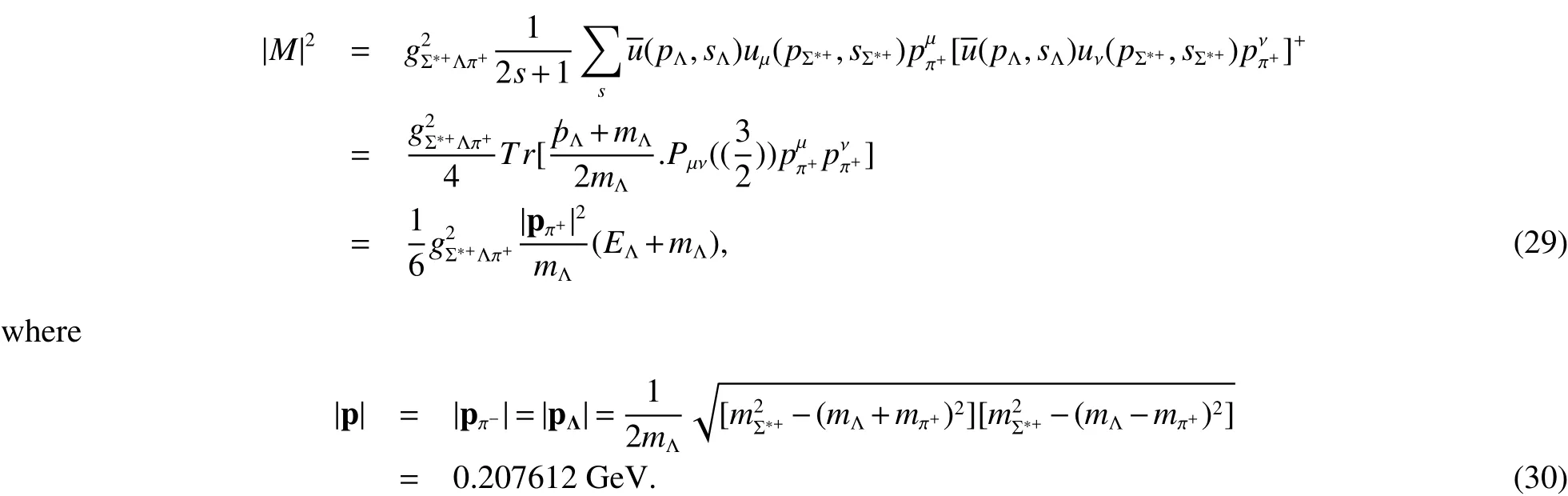
Inserting Eq.(29)into Eq.(19),we get decay width

For the process

we have

And we have

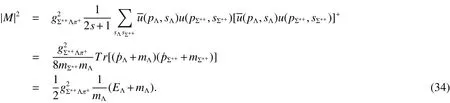
According to Eq.(19),we get

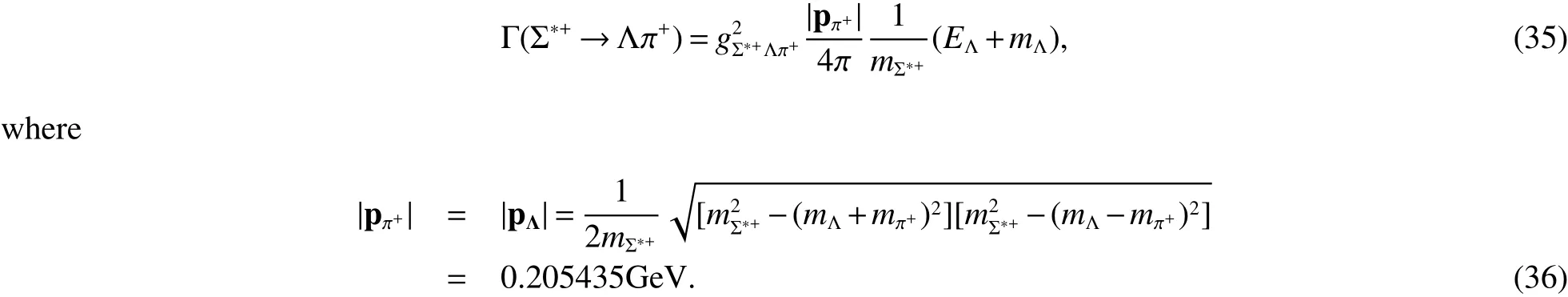
For the decay

the amplitude can be written as

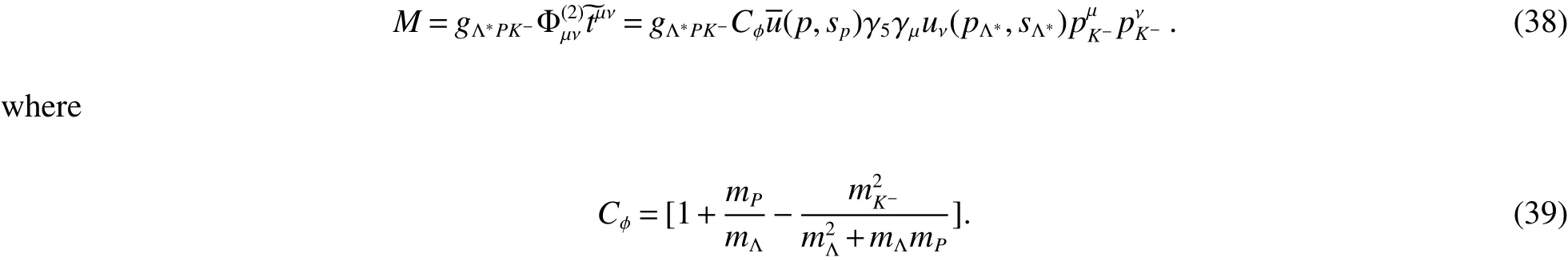
And we obtain the square of amplitude

According to Eq.(19),we obtain

For the decay

the PWA amplitude can be written as

And we obtain the following result

Inserting Eq.(44)into Eq.(19),we get decay width

3 Coupling constants

Based on the branching ratios from PDG[16],we give the estimation of the coupling constants for the(1)-(5)processes.The mass,total width,and branching ratios are shown in Table 1.

Table 1 The mass(GeV),widths(GeV),and the branching ratio for K∗0→K+π−

By using the(21)and(26),for the reaction(22),we have the

And thus we get

Table 2 The mass(GeV),widths(GeV),and branching ratios for Σ∗+ → Λπ+

Using the(21)and(31),for the process(27),we have the

Then we acquire the following result

Table 3 The mass(GeV),widths(GeV),and branching ratios(0.87)for Σ∗+→Λπ+

By using the both(21)and(35),for the process(32),we have the

So,we obtain

Table 4 he mass(GeV),widths(GeV),and branching ratios(0.279)for Λ→ K−P

By applying the(21)and(41),for the reaction process(37),we have the

Table 5 The mass(GeV),widths(GeV),and branching ratios(0.3086)for Λ → Σ∗π−

By employing both(21)and(45),for the reaction(42),we have

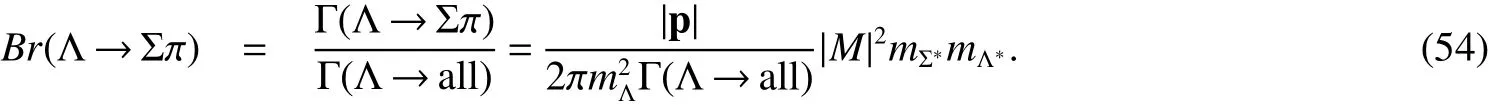
And we get

In summary,within framework of the Effective Lagrangian,we gave explicit PWA formula for the decays(1)-(5).Besides,we estimated the coupling constants for this processes by using the Branching Ratios.The value of the relevant coupling constants are give in Eqs.(47),(49),(51),(53),and(55).These information will be very useful for studying the properties and structures of these baryon states.