Quantum Phase Diagram of the Half-filled t-U-J-J0 Chain at Weak Coupling∗

WEI Xin-yu,DING Han-qin,ZHANG Jun

(College of Physics Science and Technology,Xinjiang University,Urumqi,Xinjiang 830046,China)

Abstract: Using thefield theory scenario combining bosonization and renormalization-group techniques,we study the Hubbard chain with additional anisotropic nearest-neighbor and isotropic next-nearest-neighbor spin exchange J and J0 in the weak-coupling regime.For smaller values of J0(J0<2U/3),the quantum phase diagram consists of the insulating spin-density-wave(SDW)and bond-charge-density-wave(BCDW)phases and the triplet superconducting(TS)phase.For larger J0(J0≥2U/3),a long-range charge-density-wave(CDW)phase appears,surrounded by the SDW,BCDW and TS phases.The frustrating spin exchange J0is responsible for occurrence of the CDW phase and leads to an enhancement of the dimerized BCDW phase.

Key words:t-U-J-J0chain,field theory,phase diagram,weak coupling,frustration

0 Introduction

The Hubbard chain is proposed to be the prototype of one-dimensional strongly correlated electron systems.It includes two parameters,electron hopping amplitude t and Hubbard energy U.For the repulsion U and at halffilling,the system shows a critical behavior of the insulating spin-density-wave(SDW)behavior.However,the Hubbard model alone cannot be sufficient to describe correlation Effects in spin chains,and the Heisenberg term J should be added to the original Hubbard model.This is the so-called t-U-J model,where the interactions contain both afinite on-site Coulomb repulsion U and an Effective nearest-neighbor exchange J.Compared to the Hubbard model,the t-U-J model is suggested to be more appropriate to depict the nature of magnetic correlated materials.

Over the past years,the one-dimensional t-U-J model has been widely studied.[1∼4]In the case of the isotropic antiferromagnetic exchange,Gimm et al.investigated formation of the stripe phase in the cuprate superconductors with the Hartree-Fock-Bogoliubov approximation,[5]and Dai et al.studied analytically and numerically the phase diagram,which consists of two insulating phases:a critical SDW at larger J and a bond-charge-density-wave(BCDW)at sufficiently small U for all positive J.[6]In the context of antiferromagnetic anisotropy,Ding et al.showed the existence of the longitudinal SDWzfor λ >4/3 and the transverse SDW±for λ <4/3 instead of the critical SDW phase.[7]Japaridze and Müller-Hartmann studied the case of ferromagnetic anisotropy and obtained rich phase structures containing the BCDW,SDW and triplet superconducting(TS)phases.[8]

In this paper,we extend the t-U-J model by adding a spin exchange between electrons on next nearest-neighbor(nnn)sites.In one dimension the Hamiltonian of the model reads

where cjαannihilates an electron with spin α on the lattice site j.t is the nearest-neighbor(nn)hopping integral,and U the on-site repulsion.The components of spin-1/2 operatorwith σnbeing Pauli matrices.J⊥(Jz)is transverse(longitudinal)spin-exchange interaction between electrons on nearest-neighbor(nn)sites,J0represents the spin exchange between electrons on nnn sites.Below we restrict our consideration to the case of repulsive on-site U>0 and the nnn isotropic antiferromagnetism J0>0 while the sign of the nn exchange interactions is arbitrary.We analytically study the model(1)in the weak coupling regime,where thefield theory scenario combining the bosonization with renormalization group(RG)techniques may be Effectively used.It is found that at halffilling,when the frustration J0is smaller(J0<2U/3),the phase diagram consists of the triplet superconducting phases with TS±and TS0orderings,and the insulating phases with dimerized BCDW,transverse SDW±and longitudinal SDWzinstabilities.This picture corresponds to the case of U>0 in Ref.[8]except that the relative proportion of each phase is changed.Particularly,when the frustration J0is larger(J0≥2U/3),the long-range charge-density-wave(CDW)phase appears in the triangle region surrounded by the TS±,TS0,SDW±,SDWzand BCDW phases.Moreover,the dimerized BCDW is enhanced.The result shows that the frustrated spin exchange J0changes the topological structure of the usual t-U-J chain.

1 Effective Field Theory:Bosonization and RG Analysis

To derive low-energy Effectivefield theory for the model(1),we use standard bosonization method.[9∼13]In the continuum limit the fermionfield operators decompose aswhere x=ja0(a0being the lattice spacing)and the continuous chiral fermionfields are defined by[14]

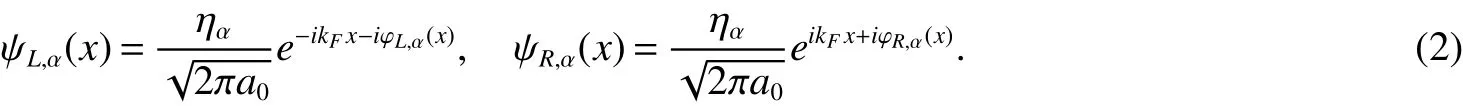
Here kFis the Fermi wave number,and the Hermitian operator ηαensures anticommutation relations of the different fermionfields.ϕL/R,αare the chiral bosonicfields,obeying the commutation relations∓iπsgn(x− x0)andWe introduce the charge and spinfieldswith

After a tedious calculation,the bosonized Hamiltonian is then given by H=Hc+Hs,where the charge and spin channels are given by

The parameters gρ/σand vc/sare the Gaussian coupling and the velocity of the elementary excitations for the charge and spin modes,respectively.The cosine terms describe the non-Luttinger-liquid-type processes including the umklapp scattering gcand backward scattering gs.Up to the leading order,the coupling constants are given by

In obtaining Eqs.(4)and(5),the strongly irrelevant charge-spin coupling terms are all omitted.

Behind bosonization,the initial lattice model Hamiltonian is mapped onto two decoupled continuum sine-Gordon models.This allows the RG techniques to analyze the low-energy excitations of the model(1)in the weak-coupling regime.Given the charge SU(2)symmetry,the one-loop RG equations are given by[14,15]

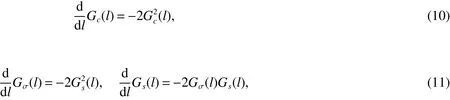
with bare values Gi(l=0)=gi/4πa0t.

Wefirst consider the phase transition in the charge degree of freedom with SU(2)symmetry,which describes Effects of the Umklapp-scattering.The charge excitations are controlled only by the Gc(l)coupling,and the equation(10)is exactly solvable.For Gc(0)>0,Gc(l)decreases to zero with increasing length scale l,and the charge excitations are gapless(∆c=0).For Gc(0)<0,the absolute value of Gc(l)grows with increasing l,and Gc(l) flows to a negative strong couplingfixed-point= −∞,accompanied by the vacuum expectation value hφci=0.This hints that the charge-gap transition takes place at the position

That is,the charge excitation spectrum is massless for Jz+2J⊥≥ 3J0−2U while it is massive for Jz+2J⊥<3J0−2U.

We then take into account the spin degree of freedom.In this case the complexity is involved due to the spin U(1)symmetry.Depending on a pair of coupled equations(11),we obtain two spin-gap transitions.One is the line

for J1⊥≤2U−3J2,and the other is the line

for J⊥>2U−3J0.Therefore,the gapless spin excitations are determined by

On the other hand,the gapped spin excitation corresponds to

According to the bare value Gs>0 or Gs<0,there are two different strong coupling sectors,which describe the relative backward scattering(∆s>0).For

Gsflows to thefixed point,=+∞,and the phasefield gets ordered with hφsi=π/2.For

Gsscales to the oppositefixed point,= −∞,and the phasefield is ordered with hφsi=0.

Table 1 Order parameters defined by fermion operators and the corresponding boson versions

2 Quantum Phase Diagram

In this section we discuss the quantum phase diagram of the model(1).In order to determine the dominant ground state phase,we introduce a set of order parametersThe corresponding Definitions and boson forms are summarized in Table 1.The exact ground state is dominated by the maximum order parameter.

We start with an analysis of the case for J0>2U/3,and the phase diagram is divided into six different sectors[see Fig.1(a)].

Fig 1 Weak-coupling quantum phase diagrams of the t-U-J-J0chain at halffilling,and(a)J0/U>2/3 and(b)J0/U<2/3

In the sector(A):The nearest-neighbor longitudinal exchange dominates over the transverse exchange,and the charge and spin excitation spectra are both massive.The expectation values of the charge and spinfields are ordered with hφci=0 and hφsi= π/2,respectively.It is easily found that the parameter OSDWztakes the maximal value,which leads to the appearance of the long-range ordered(LRO)antiferromagnetic Neel phase with SDWzcorrelation.

In the sector(B):Both the charge and spin excitation are gapped,and the expectation values of the charge and spinfields are vanishing simultaneously hφci=hφsi=0.The order parameter OBCDWtakes the maximum,and there exists the LRO dimerized BCDW phase in the ground state.

In the sector(C):The charge excitations are gapped while the spin excitations are gapless.The charge mode corresponds to the strong-coupling regime only,characterized by the vacuum expectation value hφci=0,whereas the spinfield is free.One has the maximal order parameter SDW±,and the transverse SDW±phases are realized.

In the sector(D):As in the sectors both(A)and(B),the charge and spin channels are both gapped.Whereas,the charge and spinfields are endowed with the expectation values hφci= π/2 and hφsi=0,respectively.The order parameter OCDWtakes the maximum amplitude.The LRO CDW phase is present in the ground state.

In the sector(E):The behavior of the low-energy excitations is contrary to that of the sector(C),i.e.,the charge excitation is gapless while the spin excitation is gapped.The chargefield is free but the spin mode flows to afixedpoint=+∞,accompanied by the expectation value hφsi= π/2.The parameter OTS0gets maximal amplitude,and the system is triplet superconducting phase with TS0order.

In the sector(F):Distinct from the abovefive sectors,the charge and spin channel are both gapless,and the charge and the spinfields are both free.This is the characteristic of a Luttinger liquid.The triplet superconducting phase with TS±correlations is only dominated in suppression of all the other phases.

We next analyze the J0<2U/3 case when the phase diagram comprisesfive different sectors[see Fig.1(b)].Sectors(A),(B),(C),(E)and(F)correspond to the same part given by the case of J2>2U/3,respectively.Instead,the spin-density-wave components are enhanced,while the triplet superconducting components and the dimerized BCDW phase are weakened.Particularly,the CDW phase disappears in the ground state.In this case,the phase diagram is similar to that of U>0 given by Japaridze[8].This means that when the frustration J2is smaller,the feathers of the usual t-U-J chain do not change qualitatively.

Finally,when J0=2U/3,all the transitions meet at the origin.The phases are identical to the corresponding sectors for the J2<2U/3 case except for the size of each component.

3 Summary

In this paper we have studied the one-dimensional t-U-J-J0model in the weak-coupling regime and at half bandfilling.The model considered describes a system of correlated electrons with spin-exchange interactions between on nearest-neighbor and next-nearest-neighbor sites.We focus on on-site repulsion U>0,XXZ-type anisotropy J and antiferromagnetic isotropy J0.By thefield-theoretical analysis combining bosonization and RG approach,we obtain four transitions:one in the SU(2)-symmetric charge channel and three in the U(1)-symmetric spin channel[see Fig.1].At larger J0values(J0≥ 2U/3),the phase diagram is divided into six sectors,characterized by the insulating SDW±,SDWz,CDW and BCDW as well as triplet superconducting TS±and TS0instabilities.However,when the frustrated exchange reduces to the critical value 2U/3,the CDW phase disappears.

In conclusion,our study demonstrates analytically that a next-nearest-neighbor antiferromagnetic Heisenberg exchange added to the half-filled extended Hubbard chain leads to frustration in the ground-state phase diagram,yielding a change of topological structure of the usual t-U-J model.